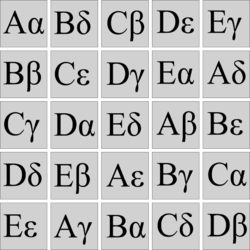Carre greco-latin

Carré gréco-latin

Carré gréco-latin d'ordre 5

Un carré gréco-latin est un tableau carré de n lignes et n colonnes remplies avec n² paires distinctes, et où chaque ligne et chaque colonne ne contient qu'un seul exemplaire. Il s'agit de la superposition de deux carrés latins orthogonaux. Si les deux carrés latins n'étaient pas orthogonaux, alors une paire pourrait apparaître plus d'une fois.

Le nom "gréco-latin" vient du fait que l'on utilisait souvent une paire composée de lettres provenant de l'alphabet grec et latin.

Sommaire

1 Exemples
- 1.1 Carrés latins orthogonaux
- 1.2 Deux carrés latins non-orthogonaux
2 Analyses et démonstrations
- 2.1 Le problème des officiers
- 2.2 Extension à d'autres ordres
3 Voir aussi
- 3.1 Articles connexes

Exemples

Carrés latins orthogonaux

Soient deux carrés latins

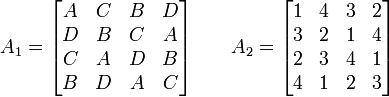
$A_1 = \begin{bmatrix} A & C & B & D \\ D & B & C & A \\ C & A & D & B \\ B & D & A & C \\ \end{bmatrix} \quad \quad A_2 = \begin{bmatrix} 1 & 4 & 3 & 2 \\ 3 & 2 & 1 & 4 \\ 2 & 3 & 4 & 1 \\ 4 & 1 & 2 & 3 \\ \end{bmatrix}$

Si $A$ est le carré $A 1$ ou $A 2$ , $A [i, j]$ correspond à l'élément en ligne $i$ , colonne $j$ de $A$ . La combinaison des carrés, $A 1 + A 2$ est définie par : l'élément en ligne $i$ et colonne $j$ de $A 1 + A 2$ est la paire $(A 1 [i, j], A 2 [i, j])$ .

Les deux carrés latins $A 1$ et $A 2$ sont orthogonaux si chaque paire du carré $A 1 + A 2$ n'apparaît qu'une seule fois.

La combinaison de deux carrés latins orthogonaux donne un carré gréco-latin (ici d'ordre 4 pour $A 1 + A 2$ ) :

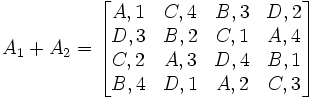
$A_1 + A_2 = \begin{bmatrix} A,1 & C,4 & B,3 & D,2 \\ D,3 & B,2 & C,1 & A,4 \\ C,2 & A,3 & D,4 & B,1 \\ B,4 & D,1 & A,2 & C,3 \\ \end{bmatrix}$

Deux carrés latins non-orthogonaux

Maintenant, nous utilisons un autre carré latin pour le second élément de la paire :

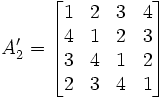
$A_2' = \begin{bmatrix} 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \\ 3 & 4 & 1 & 2 \\ 2 & 3 & 4 & 1 \\ \end{bmatrix}$

La combinaison avec le carré précédent ne donne pas un carré gréco-latin :

$A_1 + A'_2 = \begin{bmatrix} A,1 & C,2 & B,3 & D,4 \\ D,4 & B,1 & C,2 & A,3 \\ C,3 & A,4 & D,1 & B,2 \\ B,2 & D,3 & A,4 & C,1 \\ \end{bmatrix}$

On remarque en effet que la paire A,4 apparaît deux fois (et que la paire D,2 est absente). Les carrés latins $A 1$ et $A' 2$ ne sont pas orthogonaux et ne peuvent pas former un carré gréco-latin.

Analyses et démonstrations

Le problème des officiers

Problème des 36 officiers : un carré gréco-latin d'ordre 6 est impossible à résoudre

En 1782, le mathématicien suisse Leonhard Euler imagine le problème mathématique suivant. On considère six régiments différents, chaque régiment possède six officiers de grades distincts. On se demande maintenant comment placer les 36 officiers dans une grille de 6x6, à raison d'un officier par case, de telle manière que sur chaque ligne et chaque colonne contiennent tous les grades et tous les régiments.

Il s'agit d'un carré gréco-latin d'ordre 6 (un carré latin pour les régiments, un carré latin pour les grades), problème dont la résolution est impossible. Euler l'avait déjà pressenti à l'époque, sans toutefois donner une démonstration formelle à sa conjecture. Il dira :

Or, après toutes les peines qu’on s’est données pour résoudre ce problème, on a été obligé de reconnaître qu’un tel arrangement est absolument impossible, quoiqu’on ne puisse pas en donner de démonstration rigoureuse.

En 1901, le français Gaston Tarry démontre formellement l'impossibilité du résultat grâce à une recherche exhaustive des cas et par croisement des résultats.

Extension à d'autres ordres

En 1958, Bose, Parket et Shrikhande ont démontré l'existence de carrés gréco-latins pour tous les ordres, sauf pour l'ordre 2 et l'ordre 6 (la démonstration de ce dernier ayant déjà été faite par Tarry).

Voir aussi

Regardez d'autres dictionnaires:

Carré Gréco-latin — d ordre 5 Un carré gréco latin est un tableau carré de n lignes et n colonnes remplies avec n2 paires distinctes, et où chaque ligne et chaque colonne ne contient qu un seul exemplaire. Il s agit de la superposition de deux carrés latins… … Wikipédia en Français
Carré gréco-latin — d ordre 5 Un carré gréco latin est un tableau carré de n lignes et n colonnes remplies avec n2 paires distinctes, et où chaque ligne et chaque colonne ne contient qu un seul exemplaire. Il s agit de la superposition de deux carrés latins… … Wikipédia en Français
Carre latin — Carré latin Un carré latin est un tableau carré de n lignes et n colonnes remplies de n éléments distincts dont chaque ligne et chaque colonne ne contient qu un seul exemplaire. La plupart du temps, les n éléments utilisés sont les entiers… … Wikipédia en Français
Carré Latin — Un carré latin est un tableau carré de n lignes et n colonnes remplies de n éléments distincts dont chaque ligne et chaque colonne ne contient qu un seul exemplaire. La plupart du temps, les n éléments utilisés sont les entiers compris entre 0 et … Wikipédia en Français
Carre (homonymie) — Carré (homonymie) Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Carré (Homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Carré latin — Un carré latin est un tableau carré de n lignes et n colonnes remplies de n éléments distincts dont chaque ligne et chaque colonne ne contient qu un seul exemplaire. La plupart du temps, les n éléments utilisés sont les entiers compris entre 0 et … Wikipédia en Français
Carré (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Carré (homonymie) », sur le Wiktionnaire (dictionnaire universel) Issu du latin quadratus, le mot… … Wikipédia en Français
Sodoku (jeu) — Sudoku Sudoku proposé par la presse. Le sudoku (prononcé / … Wikipédia en Français
Su Doku — Sudoku Sudoku proposé par la presse. Le sudoku (prononcé / … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Carre greco-latin

Carré gréco-latin

Sommaire