Carre magique (mathematiques)

Carre magique (mathematiques)

Carré magique (mathématiques)

Page d'aide sur l'homonymie Pour les articles homonymes, voir Carré magique.
Magicsquareexample.svg

En mathématiques, un carré magique d'ordre n est composé de n2 nombres entiers généralement distincts, écrits sous la forme d'un tableau carré. Ces nombres sont disposés de manière à ce que leurs sommes sur chaque rangée, sur chaque colonne et sur chaque diagonale soient égales. Un carré magique est dit normal s'il est rempli avec les nombres entiers compris entre 1 et n2 (inclus).

Sommaire

Historique

Originaires de Chine (nommés Luoshu (洛书 le livre de la rivière Luo), représentés par différents symboles, puis symbolisés par des chiffres en Inde où furent inventés ce qu'on appelle les chiffres arabes. On les retrouve dans de nombreuses civilisations d'Asie et d'Europe avec généralement une connotation religieuse.

Les Arabes seraient les premiers, au Xe siècle, à les utiliser à des fins purement mathématiques. Ahmad al-Buni, vers 1250 leur attribue des propriétés magiques.

À la Renaissance, le philosophe allemand Cornelius Agrippa (1486-1535), parle de nouveau des carrés magiques, avec toujours une connotation religieuse, il écrit un traité De Occulta Philosophia où il expose une théorie mêlant astrologie et carrés magiques.

Simon de La Loubère, diplomate et mathématicien français, publie en 1691 le très célèbre Du Royaume de Siam. Dans ce livre qui comprend une section importante sur les mathématiques, il introduit pour la première fois dans la langue française le terme « carré magique », et expose une nouvelle méthode, dite méthode siamoise[1], de construction applicable aux carrés d'ordre impair.

Au XVIIe siècle, Le juriste et mathématicien français Pierre de Fermat étend le principe des carrés magiques aux cubes magiques. Bernard Frénicle de Bessy écrit un traité sur les carrés magiques (rédigé dans les années 1640, mais publié à titre posthume en 1693) et des tables pour tous les carrés d'ordre 4.


Description

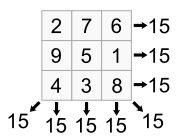
Il existe des dispositions magiques pour tout carré d'ordre n ≥ 1. Le carré d'ordre 1 est trivial, n'importe quel nombre indiqué dans l'unique case permet de satisfaire les règles. Le carré d'ordre 2 est également trivial puisqu'il n'est possible qu'en répétant le même nombre dans les quatre cases. Le plus petit cas non trivial est le carré d'ordre 3 :

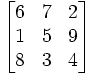
\begin{bmatrix} 6 & 7 & 2 \\ 1 & 5 & 9 \\ 8 & 3 & 4 \\ \end{bmatrix}

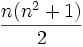La somme obtenue sur chaque ligne, colonne ou diagonale est appelée constante magique ou somme magique. La constante magique d'un carré magique normal dépend uniquement de n et vaut : {n(n^2+1) \over 2}


Démonstration

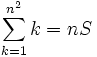
Voici une petite démonstration, très simple, permettant de retrouver cette somme. Comme le carré contient n lignes (ou n colonnes), si S est la somme de chaque ligne (ou chaque colonne), on a : \sum_{k=1}^{n^2} k = nS

Or on a : 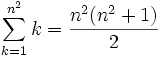\sum_{k=1}^{n^2} k = {n^2(n^2+1) \over 2}   car il s'agit de la somme des n2 premiers entiers

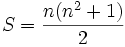
D'où : S = {n(n^2+1) \over 2}

Remarque: pour retrouver la formule de la somme S des n premiers nombres entiers, voici une astuce :

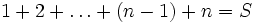
On écrit la somme des nombres dans l'ordre croissant : 1 + 2 + \ldots + (n-1) + n = S

Cette même somme peut aussi s'écrire dans l'ordre inverse: n + (n-1) + \ldots + 2 + 1 = S

En faisant la somme de ces 2 lignes, membre à membre, on obtient :

  • pour le membre de gauche : n fois (n+1)
  • pour le membre de droite : 2 fois S

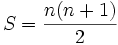
On trouve donc: S = {n(n+1) \over 2}

Pour les carrés magiques normaux d'ordre n = 3, 4, 5, 6, 7, 8, … la constante magique vaut ainsi : 15, 34, 65, 111, 175, 260, ….

Méthodes de construction

Ordre impair

Il est assez aisé de créer des carrés magiques d'ordre impair.

Placer le 1 dans la case qui se trouve sous la case du milieu du carré. Décaler d'une case vers la droite puis d'une case vers le bas pour le 2, et ainsi de suite pour le 3, puis le 4, etc. Si une case est déjà occupée, il faut revenir au nombre précédent, ne pas décaler à droite, mais descendre de 2 cases à la place.

Précision : quand on arrive au bord du carré, on continue du côté opposé (en haut ou à gauche), un peu comme si le carré était torique.

Voir ce programme de création de carré magique d'ordre impair.

Ordre pair

Créer des carrés magiques d’ordre pair est plus difficile. Le nouveau jeu mathématique "medjig" (auteur: Willem Barink, éditeur: Philos-Spiele, première édition 2006), donne une possibilité générale et ludique de créer des carrés d’ordre pair >4. Le puzzle medjig se compose de 18 pièces carrées, divisées en quatre quadrants sur lesquels il y a les nombres 0, 1, 2 et 3 en points. Chaque suite consécutive est présente trois fois. Le but du jeu est de créer des carrés 3 x 3 dans lesquels chaque rang (horizontal, vertical et diagonal) donne la somme de 9.

La méthode medjig s’exécute ainsi. Arrangez un "carré medjig" 3 x 3 (pour plus de facilité on peut se servir de toute la collection). Et puis prenez le carré magique 3 x 3 classique, divisez les cases en quatre quadrants, et remplissez les quadrants avec les nombres originaux et ses trois nombres dérivés modulo-9 jusqu'à 36, suivant l’arrangement du carré medjig. En faisant ainsi, la case originale avec le nombre 8 produit les quadrants avec les nombres 8 (= 8 + 0x9), 17 (= 8 + 1x9), 26 (= 8 + 2x9) et 35 (= 8 + 3x9). Le nombre 1 produit 1, 10, 19 et 28.

Voyez l’illustration suivante :

Ordre 3
8 1 6
3 5 7
4 9 2
Medjig 3 x 3
2 3 0 2 0 2
1 0 3 1 3 1
3 1 1 2 2 0
0 2 0 3 3 1
3 2 2 0 0 2
0 1 3 1 1 3
Ordre 6
26 35 1 19 6 24
17 8 28 10 33 15
30 12 14 23 25 7
3 21 5 32 34 16
31 22 27 9 2 20
4 13 36 18 11 29

Pour créer un carré magique d’ordre 8 il faut d’abord créer un carré medjig 4 x 4 (la somme 12). Et puis élargir par exemple le carré magique 4 x 4 de Dürer modulo-16 jusqu'à 64. Pour créer un carré d’ordre 10 il faut deux jeux de medjig. Pour l’ordre 12 on peut doubler horizontalement et verticalement un carré medjig 3 x 3, et élargir le carré magique d’ordre 6. Ainsi que l’ordre 16.


Exemples

Ordre 4

Ordre 4
16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1

Exemple de carré d'ordre 4. Totaux : 34. Ce carré magique était connu du peintre allemand Albrecht Dürer, qui l'a inclus dans sa fameuse gravure Mélancolie[1]. Il est combiné de telle sorte que pris horizontalement, verticalement ou en diagonale, la somme des nombres considérés est 34, ainsi d'ailleurs que la somme des quatre chiffres figurant dans les quatre cases centrales ou encore dans les quatre cases d'angle. Il existe un très grand nombre de possibilités de trouver, dans le carré de Dürer, le nombre 34. Ainsi prenez les quatre coins, essayez de nouveaux en prenant chaque case suivant directement un coin dans le sens des aiguilles d'une montre. Les trouver toutes vous prendra un temps certain ! Dürer réussit également à faire figurer dans les deux cases centrales de la rangée du bas la date (1514) de son œuvre.

Ordre 5

Ordre 5
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9

Exemple de carré d'ordre 5. Totaux : 65. Remarque : ce carré est «semi-diabolique» car la somme de 65 se retrouve sur toutes les diagonales brisées allant de gauche à droite. Exemple : 15 + 23 + 6 + 19 + 2 = 65. Si les diagonales brisées allant de droite à gauche présentaient cette même somme magique, le carré serait dit «diabolique». Il en existe d'ailleurs de nombreux.

Ordre 7

30 39 48 1 10 19 28
38 47 7 9 18 27 29
46 6 8 17 26 35 37
5 14 16 25 34 36 45
13 15 24 33 42 44 4
21 23 32 41 43 3 12
22 31 40 49 2 11 20

Exemple de carré d'ordre 7. Totaux : 175.

Ordre 8

52 61 4 13 20 29 36 45
14 3 62 51 46 35 30 19
53 60 5 12 21 28 37 44
11 6 59 54 43 38 27 22
55 58 7 10 23 26 39 42
9 8 57 56 41 40 25 24
50 63 2 15 18 31 34 47
16 1 64 49 48 33 32 17

Carré d'ordre 8, de Benjamin Franklin. Totaux : 260. La somme des carrés d'une même ligne est de 260 alors que la somme des quatre premières cases est de 130. Une ligne à 45° partant de la colonne de gauche et traversant les quatre premières colonnes, pour redescendre ensuite jusqu'à la colonne de droite, rencontre huit nombres d'un total de 260, quantité qui se retrouve en additionnant les nombres des cases extrêmes et des quatre cases centrales. La somme des nombres des cases de 16 carrés juxtaposés pour former l'ensemble de la figure est de 130; ce nombre se retrouve en additionnant les chiffres de quatre cases quelconques équidistantes du centre. Il est également possible de réaliser un carré magique d'ordre 8 en effectuant un parcours de case en case selon les règles de déplacement du cavalier du jeu d'échecs.


Un autre carré d'ordre 8

1 8 53 52 45 44 25 32
64 57 12 13 20 21 40 33
2 7 54 51 46 43 26 31
63 58 11 14 19 22 39 34
3 6 55 50 47 42 27 30
62 59 10 15 18 23 38 35
4 5 56 49 48 41 28 29
61 60 9 16 17 24 37 36

Carré d'ordre 8, du Général CAZALAS. Totaux : 260. C'est un carré hyper-magique car même les diagonales brisées donnent la somme caractéristique du carré magique: 260. De plus chaque sous carré de deux sur deux a un total de 130. Un exemple de diagonale "brisée" dans ce carrée: la diagonale constituée par les nombres : {8,12,51,19,42,38,29} et {61}).

Un carré parfaitement panmagique d'ordre 8

60 6 11 53 44 22 27 37
13 51 62 4 29 35 46 20
54 12 5 59 38 28 21 43
3 61 52 14 19 45 36 30
58 8 9 55 42 24 25 39
15 49 64 2 31 33 48 18
56 10 7 57 40 26 23 41
1 63 50 16 17 47 34 32

Carré panmagique d'ordre 8, de Willem Barink. Totaux : 260. C'est un carré spécial, présentant (presque) toutes les propriétés panmagiques concevables. Aussi les 4 quadrants du carré sont des carrés panmagiques. Les diagonaux partielles et les diagonaux franklines (redescendant chez les diamètres) ont un total de 260: 18 + 25 + 45 + 38 + 59 + 52 + 8 + 15 = 260. De plus, il y a seulement deux sommes pour les paires de nombres consécutives dans aussi les lignes horizontales (66, 64) que les lignes verticales (73, 57).

Carré panmagique d‘ordre 12

Ordre 12 panmagique
138 8 17 127 114 32 41 103 90 56 65 79
19 125 140 6 43 101 116 30 67 77 92 54
128 18 7 137 104 42 31 113 80 66 55 89
5 139 126 20 29 115 102 44 53 91 78 68
136 10 15 129 112 34 39 105 88 58 63 81
21 123 142 4 45 99 118 28 69 75 94 52
130 16 9 135 106 40 33 111 82 64 57 87
3 141 124 22 27 117 100 46 51 93 76 70
134 12 13 131 110 36 37 107 86 60 61 83
23 121 144 2 47 97 120 26 71 73 96 50
132 14 11 133 108 38 35 109 84 62 59 85
1 143 122 24 25 119 98 48 49 95 74 72

Exemple de carré panmagique d'ordre 12 de Willem Barink. Totaux : 870. Un carré contenant presque toutes les propriétés panmagiques concevables, sauf les diagonaux franklines. Le carré se compose de 9 carrés 4x4 panmagiques. Commençant à une case impaire dans une ligne, la somme de 4 nombres consécutives est 290 (=1/3 de la somme totale de la ligne). Suivant l'installation des nombres 1, 2, 3, 4......, 144 on peut s' apercevoir que la figure symétrique est de forme identique que celle du carré ci-dessus panmagique 8x8. On peut construire tous les carrés d'ordre 4k suivant cette symétrie.

Curiosités

Curiosité des carrés magiques
  • Si l'on relie les nombres du carré magique dans l'ordre croissant, on obtient une figure symétrique (voir image ci-contre). Exception pour le carré magique de medjig plus haut, car il y a plusieurs fois certains nombres, par conséquent, on ne peut pas déterminer le tracé de la figure.
  • La théorie des groupes a été utilisée pour trouver les carrés magiques d'un ordre donné à partir d'un de ceux-ci: voir [2] (en anglais).
  • En mentalisme, certains artistes exécutent des carrés magiques lors de leur show. Un spectateur pense ou dit un nombre, l'artiste fait un carré magique en quelques secondes.

Carrés magiques premiers

Les carrés magiques peuvent également être intégralement constitués de nombres premiers [2] comme le montre l'exemple ci-dessous appelé "Carré magique de Skalli", du nom de son inventeur, Ali Skalli. Il est qualifié de "diabolique" du fait que de nombreuses symétries y figurent (entre autres, croix pleines et déliées, en diagonale et en verticale), ainsi que les translations horizontales et verticales de toutes celles-ci. Le nombre magique est 13665.

Skalli 5 x 5
2087 2633 2803 2753 3389
2843 2729 3347 2099 2647
3359 2113 2687 2819 2687
2663 2777 2699 3373 2153
2713 3413 2129 2621 2789

Par conjecture, un nombre infini de carrés magiques de Skalli existent, mais aucune démonstration n'existe à ce jour. En revanche, il est possible d'en produire aisément un nombre considérable, non calculable en l'absence de démonstration.

Carrés magiques multiplicatifs de Skalli

La méthode non itérative de Skalli est également applicable aux carré magiques multiplicatifs. Voici un exemple 7x7 dont entre autres, les produits de chaque ligne, chaque colonne et chaque diagonale est 6'227'020'800:

Skalli multiplicatif 7 x 7
27 50 66 84 13 2 32
24 52 3 40 54 70 11
56 9 20 44 36 65 6
55 72 91 1 16 36 30
4 24 45 60 77 12 26
10 22 48 39 5 48 63
78 7 8 18 40 33 60

Par "coquetterie", le 1 est placé au centre, mais la méthode permet de le placer où l'on veut, tout comme elle permet de générer des carrés magiques avec n'importe quel nombre magique, y compris réel ou complexe comme ci-dessous

Carrés magiques multiplicatifs de nombres complexes

Le carré magique complexe ci-dessous donne le produit magique de -352'507'340'640 - 400'599'719'520 i, toujours (entre autres) sur chaque ligne, chaque colonne et chaque diagonale:

Skalli multiplicatif 7 x 7 de nombres complexes [3]
21+14i -70+30i -93-9i -105-217i 16+50i 4-14i 14-8i
63-35i 28+114i -14i 2+6i 3-11i 211+357i -123-87i
31-15i 13-13i -103+69i -261-213i 49-49i -46+2i -6+2i
102-84i -28-14i 43+247i -10-2i 5+9i 31-27i -77+91i
-22-6i 7+7i 8+14i 50+20i -525-492i -28-42i -73+17i
54+68i 138-165i -56-98i -63+35i 4-8i 2-4i 70-53i
24+22i -46-16i 6-4i 17+20i 110+160i 84-189i 42-14i

Ce carré magique est entièrement construit de manière alléatoire, et peut donc se décliner à l'infini, y compris avec des parties réelles et imaginaires appartenant à l'ensemble des nombres réels.

Notes et références

  1. ↑ (en)Voir article de Wikipédia anglophone
  2. ↑ Carré 5x5 de nombres premiers Carrés et cubes magiques d'Ali Skalli
  3. ↑ Carré 8x8 multiplicatif de nombres complexes Carrés et cubes magiques d'Ali Skalli

Voir aussi

Articles connexes

Liens externes

Bibliographie

  • (en) Illustrations de la première édition anglaise du Royaume de Siam de Simon de la Loubère : Carrés magiques
  • Carrés magiques, carrés latins et eulériens : histoire, théorie, pratique. Jacques Bouteloup, Éditions du Choix, 1991.ISBN 2-909028-02-x
  • Portail des mathématiques Portail des mathématiques


Ce document provient de « Carr%C3%A9 magique (math%C3%A9matiques) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Carre magique (mathematiques) de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Carré Magique (Mathématiques) — Pour les articles homonymes, voir Carré magique. En mathématiques, un carré magique d ordre n est composé de n2 nombres entiers généralement distincts, écrits sous la forme d un tableau carré. Ces nombres sont disposés de manière à …   Wikipédia en Français

  • Carré magique (Mathématiques) — Pour les articles homonymes, voir Carré magique. En mathématiques, un carré magique d ordre n est composé de n2 nombres entiers généralement distincts, écrits sous la forme d un tableau carré. Ces nombres sont disposés de manière à …   Wikipédia en Français

  • Carré magique ( Mathématiques ) — Carré magique (mathématiques) Pour les articles homonymes, voir Carré magique. En mathématiques, un carré magique d ordre n est composé de n2 nombres entiers généralement distincts, écrits sous la forme d un tableau carré. Ces nombres sont… …   Wikipédia en Français

  • Carré magique (mathématiques) — Pour les articles homonymes, voir Carré magique. un exemple de carré magique. En mathématiques, un carré magique d ordre n est composé de …   Wikipédia en Français

  • Carré magique (Economie) — Carré magique (mathématiques) Pour les articles homonymes, voir Carré magique. En mathématiques, un carré magique d ordre n est composé de n2 nombres entiers généralement distincts, écrits sous la forme d un tableau carré. Ces nombres sont… …   Wikipédia en Français

  • Carre magique d'inverses de nombres premiers — Carré magique d inverses de nombres premiers En mathématiques, un inverse est le nombre 1 divisé par un autre nombre (aussi appelé fraction unitaire), comme 1/3 ou 1/7. En base 10, le reste, et donc les chiffres, de 1/3 se répètent une fois  …   Wikipédia en Français

  • Carré Magique D'inverses De Nombres Premiers — En mathématiques, un inverse est le nombre 1 divisé par un autre nombre (aussi appelé fraction unitaire), comme 1/3 ou 1/7. En base 10, le reste, et donc les chiffres, de 1/3 se répètent une fois : 0,3333... Néanmoins, la période répétitive… …   Wikipédia en Français

  • Carre magique plus que parfait — Carré magique plus que parfait En mathématiques, un carré magique plus que parfait est un type de carré magique avec deux propriétés supplémentaires (où n désigne la taille du carré): La somme sur chaque sous carré de taille 2 x 2 vaut 2S où S =… …   Wikipédia en Français

  • Carré Magique Plus Que Parfait — En mathématiques, un carré magique plus que parfait est un type de carré magique avec deux propriétés supplémentaires (où n désigne la taille du carré): La somme sur chaque sous carré de taille 2 x 2 vaut 2S où S = n2 + 1. La somme de chaque… …   Wikipédia en Français

  • Carre magique — Carré magique Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Carré magique en mathématiques. Carré magique de Kaldor en économie. Carré magique utilisant des mots. Carré magique de l équipe de France… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”