Calculatrice mécanique

Exemple de calculatrice mécanique : la Divisumma 24 d'Olivetti, datant de 1964. Le capot est retiré afin de faire ressortir le mécanisme de la machine. Les moteurs électriques sont à l’arrière

Calculatrice mécanique, machine à calculer et machine arithmétique sont trois noms décrivant une calculatrice dont le fonctionnement est principalement mécanique. Ils ne différent que par la période pendant laquelle ils furent utilisés.

Machine arithmétique fut utilisé à partir de 1642. Elle fut suivit de machine à calculer, qui fut utilisé pendant tout le XIX^e siècle et pendant la première moitié du XX^e siècle. Calculatrice mécanique, un néologisme de la deuxième moitié du XX^e siècle, fut utilisé pour différentier les machines à calculer mécaniques des machines à calculer électroniques (1961)^[1].

Historique

Dessin de boulier ; le nombre représenté est 6 302 715 408).

Origines

Les abaques, outils d'aide au calcul, remontent à plusieurs millénaires. Outre le fait de compter sur ses doigts, le plus ancien outil de calcul est probablement le bâton de comptage. Le boulier est inventé avant 2000 av. J.-C.

Des calculateurs analogiques sont construits aux époques antique et médiévale afin de réaliser des calculs astronomiques, comme la machine d'Anticythère ou l'astrolabe grecs (vers 150-100 av. J.-C.), les outils conçus par Al-Biruni comme le planisphère (vers 1000), l'équatorium et l'astrolabe universel indépendant de la latitude d'Al-Zarqali (vers 1015) ou la tour-horloge astronomique de Su Song (vers 1090).

Le XVII^e siècle

Le XVII^e siècle, un siècle pivot

Le XVII^e siècle fut un siècle tournant dans l'histoire des machines à calculer. D'un côté il vu la création d'un ensemble d'outils d'aide au calcul révolutionnaires comme les tables de logarithmes et les règles à calcul qui, de part la facilité qu'ils donnaient aux mathématiciens et aux physiciens de multiplier et de diviser, dominèrent et freinèrent le développement des machines à calculer^[2] jusqu'à la commercialisation de l'arithmomètre en 1851. D'un autre côté, il vit l'invention de la machine à calculer en 1642 qui lança le développement du calcul mécanique d'abord en Europe, puis dans le monde entier.

Aide au calcul

John Napier introduisit les logarithmes et les tables de logarithmes en 1614 avec la publication de Mirifici logarithmorum canonis descriptio (les logarithmes transforment les multiplications en de simples additions et les divisions en soustractions). C'est pendant l’écriture de ce livre, qui demandait beaucoup de calculs, qu'il inventa les batons de Napier, qui furent décrit dans le livre Rabdologiæ seu Numerationis per Virgulas libri duo (1617).

La règle à calcul, qui utilise le principe des logarithmes, fut inventée en 1622 par William Oughtred. Cet outil permet de réaliser des opérations de multiplication et de division de façon significativement plus rapide que précédemment et resta en usage jusqu'à l'invention de la calculatrice de poche vers 1970.

Premières machine à calculer

En 1642, Blaise Pascal inventa la machine à calculer^[3], dénommée machine arithmétique, roue pascaline et enfin pascaline, elle marque l'origine du calcul mécanique.

C'est en cherchant à y ajouter une interface de multiplication et de division automatique que Leibniz inventa son fameux cylindre cannelé vers 1671^[4] et qu'il fut le premier à décrire une roue à nombre variable de dents en 1685^[5]. Il construisit une machine qui pouvait multiplier deux nombres d'une manière directe, mais il ne put la commercialiser ; l’étude de cette machine à la fin du XIX^e siècle montra qu'elle n’était pas tout à fait finie.

Thomas de Colmar s'inspira des travaux de Pascal et de Leibniz quand il conçut son arithmomètre en 1818 et Dorr E. Felt substitua les roues d'entrée de la pascaline par un clavier à touche pour son comptomètre en 1884.

Le XVIII^e siècle

Le XVIII^e siècle vu les premières machines à calculer complètes qui pouvaient faire les quatre opérations d’arithmétique automatiquement. Elles utilisaient soit des cylindres cannelés de Leibniz ou des roues à nombre variable de dents. Quelques essais de commercialisation n'eurent pas de succès.

XIX^e siècle

Chronologie des machines à calculer de bureau en production au XIX^e siècle.

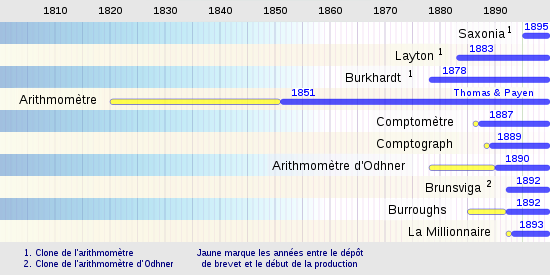
En 1820 Thomas de Colmar invente l'Arithmomètre. Il permet de multiplier et de diviser un opérande de quelques chiffres par un opérateur à un chiffre. Thomas passera 30 ans et 300.000 francs pour améliorer cette machine^[6]. Incidemment, il acheta le Château de Maisons-Laffitte en 1848 pour la moitié de cette somme^[7].

En 1834, Charles Babbage associe les cartes du métier Jacquard à une machine à calculer et imagine sa machine analytique, l’ancêtre des ordinateurs. Il la dote de mémoires, d'imprimantes, d'une unité centrale de calcul, d'un lecteur de cartes Jacquards pour les données et d'un autre pour les cartes de programmes (il crée ainsi le premier langage machine de programmation)^[8]. Cette machine ne fut jamais construite mais cent ans plus tard, en 1937, Howard Aiken en fit mention plusieurs fois quand il convint IBM de se lancer dans le développement d'ordinateurs avec la construction de l'Harvard Mark I ^[9][10].

En 1851 Thomas simplifie l'arithmomètre en ôtant le chiffre multiplicateur. Ce n'est plus qu'une machine à addition et soustraction directes mais grâce à son plateau de résultat mobile, elle permet de faire des multiplications et des divisions d'une manière simple et rapide. Chaque machine est dotée d'un numéro de série et des notices d'instructions sont imprimées. C'est grâce à sa simplicité, à sa fiabilité et à sa robustesse que les banques, les compagnies d'assurances, les bureaux du gouvernement commencent à utiliser une machine à calculer dans leurs opérations journalières. L'arithmomètre devint la première machine à calculer commercialisée ; le début de sa production en série créa l'industrie de la machine à calculer. L'arithmomètre n'aura pas de concurrent pendant quarante ans (sauf pour deux de ses clones vers la fin de cette période).

En 1873 W.T. Odhner crée l'Arithmomètre d'Odhner en redessinant l'Arithmomètre autour de roues à nombres variables de dents tout en conservant le même interface d'utilisation. Sa commercialisation commença en 1890. Au fil du temps, cette machine sera clonée dans le monde entier et des millions d'exemplaires seront vendus, jusque dans les années 1970.

Le Comptomètre est breveté aux États-Unis en 1886 ; en 1887 il devient le premier appareil à clavier direct à être commercialisé. Un clavier direct est très rapide car chaque touche ajoute sa valeur au total dés qu'elle est enfoncée (au lieu d'avoir à actionner une manette) et plusieurs touches peuvent êtres utilisées à la fois. Il deviendra la première machine à calculer à avoir un organe de calcul électronique en 1961 (ANITA mark VII de Sumlock Comptometer Ltd)

La Millionnaire est introduite en 1893. Elle permet la multiplication directe.

Le concept de la calculatrice à crosses est inventé par Louis Troncet en 1889. Il conduit à des calculatrices mécaniques plates et portables. Elles sont popularisés dans les années 1920 avec l'Addiator.

XX^e siècle

Calculatrice mécanique en 1914.

Entre 1900 et 1960, les calculatrices mécaniques se développent, leur mécanisme s'affine. Certains appareils possèdent des moteurs électriques. De nombreuses calculatrices possèdent une rangée entière de touches numérotées par chiffre. Dalton introduit la première machine à n'utiliser que 10 touches numériques, en 1902. La Facit-T est la première machine de ce type à rencontrer un succès commercial, en 1932. La Divisumma-14 d'Olivetti est la première machine à posséder à la fois 10 touches et un dispositif d'impression du résultat.

En 1948, la Curta est introduite. Il s'agit d'une calculatrice miniaturisée, qui tient dans la main et qui est opérée par une manivelle, comme un moulin à café.

Déclin

À la suite du développement des calculateurs électroniques, le marché des calculatrices mécaniques décroît, mais les appareils continuent à se vendre jusqu'au début des années 1970. Les appareils de type Comptomètre sont souvent conservés plus longtemps, leurs opérateurs entrainés étant capables d'effectuer les calculs plus rapidement qu'avec une calculatrice électronique. Néanmoins, le développement des ordinateurs les rend finalement obsolètes.

Galerie d'images

• 

  Facit NTK (1954).

• 

  Triumphator CRN1 (1958).

• 

  Walther WSR160 (1960).

• 

  Nisa K.

• 

  Contex 10.

• 

  Curta (1948).

Exemples d'utilisation

Principes

Calculatrice mécanique produite par la société suédoise Facit.

Les calculatrices mécaniques fonctionnent, pour la plupart, sur des principes similaires. Elles sont capables d'effectuer les quatre types d'opérations usuelles : addition, soustraction, multiplication et division.

Les paragraphes qui suivent décrivent des exemples d'opérations sur une machine de type Facit, une compagnie suédoise. Cette machine dispose de trois cadrans : celui en haut à gauche permet d'afficher les résultats, celui de droite s'incrémente en fonction du nombre de tours de manivelle et celui du bas affiche les nombres écrits avec le clavier. Trois manettes permettent d'effacer séparément chacun des trois cadrans et une manivelle permet de réaliser les opérations. Les nombres sont entrés à l'aide d'un clavier numérique similaire à celui d'une machine à écrire. Deux touches fléchées permettent de décaler d'une dizaine vers la droite ou la gauche le nombre utilisé par la manivelle. Cette disposition se retrouve sur de nombreux modèles de calculatrices mécaniques.

Addition

L'opération 252+49 s'effectue ainsi :

1. Entrer le nombre 252. Celui-ci s'affiche sur l'écran du bas.
2. En tournant la manivelle correspondante, reproduire ce nombre sur l'écran de résultat.
3. Réinitialiser l'écran du bas avec la manette correspondante.
4. Entrer le nombre 49. Celui-ci s'affiche sur l'écran du bas.
5. En tournant la manivelle appropriée, ce nombre est ajouté sur l'écran de résultat : 301.

Soustraction

L'opération 252-49 s'effectue de la manière suivante :

1. Entrer le nombre 252. Celui-ci s'affiche sur l'écran du bas.
2. En tournant la manivelle correspondante, reproduire ce nombre sur l'écran de résultat.
3. Réinitialiser l'écran du bas avec la manette correspondante.
4. Entrer le nombre 49. Celui-ci s'affiche sur l'écran du bas.
5. En tournant la manivelle appropriée à l'envers, ce nombre est retranché de l'écran de résultat : 203.

Multiplication

Pour effectuer l'opération 252×49, trois méthodes sont possibles :

• Méthode fastidieuse, en considérant la multiplication par 49 comme l'équivalent de 48 additions successives de 252 sur lui-même :

1. Entrer le nombre 252. Celui-ci s'affiche sur l'écran du bas.
2. Tourner 49 fois de suite la manivelle appropriée. L'écran de droite indique le nombre de tours. Au final, l'écran de gauche indique le résultat obtenu : 12 348.

• Méthode rapide, en décomposant 49 sous la forme 4×10+9 :

1. Entrer le nombre 252. Celui-ci s'affiche sur l'écran du bas.
2. Traiter le chiffre des unités de 49 : tourner 9 fois la manivelle. L'écran de droite indique le nombre de tours (9) et l'écran de gauche indique le résultat obtenu : 2 268.
3. Appuyer une fois sur la flèche de gauche : cette opération permet d'ajouter à chaque tour de manivelle le nombre 2 520 et non plus 252.
4. Traiter le chiffre des dizaines de 49 : tourner 4 fois la manivelle. L'écran de droite indique le nombre de tours et l'écran de gauche indique le résultat final : 12 348.

• Méthode experte, en considérant 49 comme 5×10-1 :

1. Entrer le nombre 252. Celui-ci s'affiche sur l'écran du bas.
2. Appuyer une fois sur la flèche de gauche : chaque tour de manivelle ajoute alors 2 520 à l'écran de résultat.
3. Tourner 5 fois la manivelle. L'écran de droite indique le nombre de tours (50) et l'écran de gauche indique le résultat obtenu : 12 600.
4. Appuyer une fois sur la flèche de droite pour revenir aux unités : chaque tour de manivelle ajoute 252 à l'écran de résultat.
5. Tourner 1 fois la manivelle à l'envers. L'écran de droite indique le nombre de tours (49) et l'écran de gauche indique le résultat final : 12 348.

Division

Pour effectuer l'opération 252/49 :

1. Entrer le nombre 252. Celui-ci s'affiche sur l'écran du bas.
2. Tourner une fois la manivelle. Le nombre 252 est écrit sur les cadrans de gauche et du bas, le nombre 1 est écrit à droite.
3. Effacer l'écran du bas et l'écran de droite à l'aide des manivelles appropriées.
4. Entrer le nombre 49. Celui-ci s'affiche sur l'écran du bas.
5. Tourner la manivelle à l'envers jusqu'à ce que le cadran de gauche indique un nombre inférieur à 49.
6. le quotient s'écrit sur le cadran de droite : 5. Le reste est affiché sur celui de gauche : 7.

Annexes

Notes

Sources bibliographiques

• Robert Ligonnière, Préhistoire et histoire des ordinateurs, Paris, Robert Laffont, 1987 (ISBN 978-2-221-05261-7) (LCCN 88119489) 
• Jean Marguin, Histoire des instruments et machines à calculer, Hermann, 1994 (ISBN 978-2-7056-6166-3) 
• René Taton, Le calcul mécanique. Que sais-je ? n° 367, Presses universitaires de France, 1949 
• René Taton, Le calcul mécanique. Que sais-je ? n° 367, Presses universitaires de France, 1963 
• René Taton, Histoire du calcul. Que sais-je ? n° 198, Presses universitaires de France, 1969 
• Edouard Sitzmann, Dictionnaire de biographie des hommes célèbres de l’Alsace, t. 1er, Rixheim, Alsace, Imprimerie F. Sutter & Cie, 1909 
• (en) Jekuthiel Ginsburg, Scripta Mathematica (Septembre 1932-Juin 1933), Kessinger Publishing, LLC, 2003 (ISBN 978-0-7661-3835-3) 
• (en) David Eugene Smith, A Source Book in Mathematics, New York and London, McGraw-Hill Book Company, Inc., 1929 
• (en) Brian Randell, The origins of Digital computers, Selected Papers, Berlin, Heidelberg, New York, Springer-Verlag, 1973 (ISBN 978-3-540-06169-4) (LCCN 73075808) 

Liens internes

• Calculatrice
• Thomas Fowler (inventeur) (en)

Liens externes

•  Calculatrices mécaniques sur Commons

• Portail des mathématiques
• Portail du génie mécanique