Pascaline

Pour les articles homonymes, voir Pascaline (homonymie).

Une Pascaline, signée par Pascal en 1652, visible au Musée des arts et métiers à Paris.

Blaise Pascal est l'inventeur de la machine à calculer^[1],[2]. C'est en 1642, à l'âge de dix neuf ans, qu'il en conçut l’idée^[3] voulant soulager la tâche de son père qui venait d’être nommé surintendant de la Haute-Normandie par le Cardinal de Richelieu et qui devait remettre en ordre les recettes fiscales de cette province^[4] ; dénommée successivement machine d’arithmétique, roue pascaline puis pascaline^[5], elle permettait d’additionner et de soustraire deux nombres d'une façon directe et de faire des multiplications et des divisions par répétitions.

En 1645, après trois ans de recherche et 50 prototypes, Pascal présenta sa première machine en la dédiant au chancelier de France, Pierre Séguier^[6]. Il construisit une vingtaine de pascalines dans la décennie suivante souvent en les perfectionnant; neuf de ces machines ont survécu jusqu’à nos jours^[7]. Un privilège royal, promulgué par Louis XIV^[8], lui donna l'exclusivité de la production de machines à calculer en France^[9],[10].

Dés 1649 Pascal chercha à réduire le coût de fabrication de sa machine, sachant que sa cherté la rendait inutile au public, mais, en 1654, après un traumatisme crânien sévère^[11], reçu au cours d'un accident de carrosse , il se retira du monde scientifique et abandonna ce projet, entre autres, et se concentra sur la philosophie et sur la religion, il avait trente et un ans.

L'introduction de la Pascaline marque le point de départ et lança le développement du calcul mécanique d'abord en Europe, puis dans le monde entier. Ce développement, qui passa des machines à calculer aux calculatrices électriques et électroniques des siècles suivant, culminera avec l'invention du microprocesseur par Intel en 1971^[12],[13].

La Pascaline fut à l'origine de beaucoup de machines et d'inventions clés de cette industrie. En effet, c'est en cherchant à y ajouter une interface de multiplication et de division automatique que Leibniz inventa son fameux cylindre cannelé (1671)^[14]; Thomas de Colmar s'inspira des travaux de Pascal et de Leibniz quand il conçut son arithmomètre (1818) et Dorr E. Felt substitua les roues d'entrée de la pascaline par un clavier à touche pour son comptomètre (1884). Elle fut aussi améliorée constamment, surtout avec les machines du docteur Roth^[15] vers 1840, et enfin avec des machines portables jusqu'à l'avènement des premières calculatrices électroniques.

Précurseurs de la machine à calculer

De l'antiquité à la renaissance

Odomètre de Léonard de Vinci (avant 1519)

Toutes les machines à engrenage antérieures à la pascaline font partie des précurseurs de la machine à calculer. Une liste sommaire se doit d'inclure la Machine d'Anticythère d'avant 87 av. J.-C., les horloges mécaniques à partir du XIII^e siècle et les astrolabes. Ces machines permirent aux sociétés qui les produisaient de se familiariser avec la notion de mouvements à engrenage, au travail minutieux des métaux qui les composaient et à leur assemblage^[16].

Certains instruments de mesure et certains automates furent aussi des précurseurs de la machine à calculer.

Un carrosse de la Dynastie Han avec deux figurines sonnant les distances.

Un odomètre, instrument qui mesure la distance parcourue par un véhicule, fut décrit pour la première fois par le Romain Vitruve vers 25 av. J.-C. ; dans le dixième volume de son De architectura il présente un odomètre, installé dans un chariot, qui consistait en une série de roues dentées liées par une progression de retenue. La première roue était entraînée par une des roues du chariot et la dernière faisait tomber une petite boule dans un sac à chaque mille romain parcouru^[17].

Un texte chinois du III^e siècle décrit un chariot monté de deux figurines en bois et d'un mécanisme qui faisait donner un coup de tambour à une des figurines tous les lis et qui faisait sonner une cloche à l'autre tous les dix lis^[18].

Vers la fin du X^e siècle, le moine français Gerbert d'Aurillac^[19], dont l'abaque enseigna les chiffres arabes aux européens^[20], rapporta d’Espagne les plans d'une machine à calculer (automate) inventée par les Maures dont l'organe de sortie avait la forme d'une tête parlante et qui répondait par oui ou par non aux questions qu'on lui posait (arithmétique binaire) mais les avis diffèrent sur son existence^[21].

De nouveau, au XIII^e siècle, les moines Albert le Grand et Roger Bacon construisirent des androïdes parlants, mais ces instruments n'eurent pas de lendemain (Albert le Grand se plaignit d'avoir gâché 40 ans de travail quand Thomas d'Aquin, terrifié par sa machine, la détruisit)^[22].

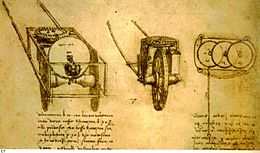
Léonard de Vinci dessina un odomètre avant 1519.

En 1525, l'artisan français Jean Fernel créa le premier podomètre qui est une machine qui compte le nombre de pas d'un homme ou d'un cheval ; il avait la forme d'une montre et avait quatre cadrans d'affichage (unités, dizaines, centaines, milliers) liés par un système de progression de retenue^[23].

Pascal versus Schickard

Horloge à calculer de Schickard

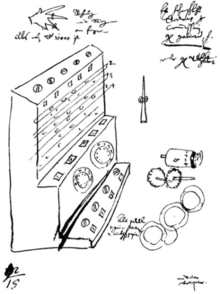
À partir de l'introduction de la Pascaline et pendant plus de trois siècles Pascal fut considéré comme l'inventeur de la machine à calculer^[24]; puis en 1957, Dr. Franz Hammer, un expert allemand des travaux de Kepler, révéla l'existence de deux lettres écrites par Wilhelm Schickard à son ami Johannes Kepler, qui précédaient les travaux de Pascal d'une vingtaine d’années, et qui contenaient le dessin d'une même horloge à calculer inconnue^[25]. L'existence de cette machine resta inconnue pendant plus de trois siècles car elle fut détruite dans un incendie en 1624, pendant sa construction par Johann Pfister un artisan local et Schickard décida de ne pas en faire construire une autre.

Le professeur von Freytag Loringhoff, de l'université de Tübingen construisit la première reproduction mais il fallut qu'il perfectionne le système de retenue à une dent qui:

« ... présente une multitude de problèmes pour toute personne voulant construire une machine à calculer basée sur ce principe. Le problème le plus important vient du fait que la dent unique de la roue mutilée doit s'insérer entre les dents de la roue intermédiaire, la faire tourner de 36 degrés (un dixième de tour), puis doit se retirer, tout cela en ne tournant elle-même que de 36 degrés. La solution la plus simple à ce problème est de composer la roue intermédiaire de deux roues, une avec des dents longues et une avec des dents courtes accouplée à une détente à ressort (similaire au pointeur/curseur utilisé dans une roue de loterie) ce qui permet aux pignons de s’arrêter dans des positions fixes. Nous ne savons pas si Schickard utilisa ce mécanisme, mais il marche bien sur les reproductions de von Freytab Loringhoff. »

— Michael R. Williams^[26], History of Computing Technology, IEEE, 1997

Sans ce système de retenue perfectionné au XX^e siècle, et qui ne figure ni dans les lettres de Schickard, ni dans ses dessins, les reproductions de son horloge à calculer n'auraient pas fonctionné. Mais un second problème fut découvert durant l'utilisation des reproductions ;

« Il est quasi-certain que Pascal ne connaissait rien de la machine de Schickard... »

« Il semble que Pascal ait réalisé dés le départ qu'une roue de propagation à une dent, comme celle utilisée par Schickard, n'était pas une solution adéquate pour le report de retenue. Une roue de propagation à une dent marche bien si la retenue est propagée sur un petit nombre de roues mais quand la retenue est propagée sur plusieurs roues consécutives de l'accumulateur la force requise pour faire avancer la machine est d'une telle magnitude qu'elle peut endommager ses rouages délicats »

— Michael R. Williams^[27], History of Computing Technology, IEEE, 1997

Les deux machines utilisent un mode d'inscription direct (les opérations sont effectuées pendant l'entré des données) et donc les reports de retenues se font durant l'inscription des opérandes:

• Dans la machine de Pascal chaque roue est totalement indépendante et donc «  il est aussi facile de faire mouvoir mille et dix mille roues tout à la fois... que d'en faire mouvoir une seule ». Cette indépendance est réalisée grâce à un sautoir à contrepoids « ...qui était en avance sur son temps puisqu'il effectuait les reports en cascade, évitant ainsi le blocage de la machine en cas de report multiple^[28] ». Il faut noter qu'avant toute opération la remise à zéro de la pascaline prouve que son mécanisme est en parfait état de fonctionnement car l’opérateur doit mettre toutes les roues de sa machine à leur maximum^[29] (ce qui fait 99.999.999 sur celle de Marguerite Pérrier) puis il doit ajouter 1 à la roue des unités^[30] ce qui entraîne un report de retenue sur toutes les roues.
• Schickard avait basé sa machine sur le principe des horloges avec des roues moins délicates et plus lourdes, elles-mêmes connectées à des roues d'inscriptions et de résultats. Pendant un report de retenue, l'ensemble des roues d'un chiffre est connecté à l'ensemble des roues d'un des chiffres voisins grâce à une roue à une dent. L'inertie cumulative de toutes ces roues « pouvait endommager la machine si une retenue devait être propagée sur beaucoup de chiffres, comme par exemple pendant l'addition de 1 à un nombre comme 9.999^[31] ».

Clément Ader: précurseur de l'aviation

Les frères Wright: premier vol

Bien que la machine de Schickard soit antérieure, Pascal est toujours l'inventeur de la machine à calculer car,

« ...dans l'état actuel de la question, nous paraît-il légitime de considérer Schickard comme le principal précurseur du calcul mécanique, mais non comme l'inventeur de la machine à calculer. Une invention ne peut en effet être authentifiée que si elle a été présentée á des témoins dignes de foi, puis diffusée et mise en service... »

— René Taton^[32], 1963

‎Tout comme les frères Wright, crédités pour le premier vol et donc pour l'invention du premier avion, bien que Clément Ader vola treize ans plus tôt, Blaise Pascal est considéré comme l'inventeur de la machine à calculer car il présenta la première machine qui comportait tous les éléments requis pour son bon fonctionnement, pour son utilisation et pour ses futures améliorations, une machine primitive mais complète avec un design prêt à évoluer.

Johannes Kepler, le destinataire de la lettre de Schickard, mourut avant l'introduction de la pascaline mais il fut témoin d'une dualité similaire (précurseur/inventeur) avec l'invention des logarithmes:

« ...les calculs effectués par Justus Byrgius l’amenèrent sur le chemin de ces même logarithmes des années avant que le système de Napier apparaisse; mais ... au lieu de fièrement présenter son enfant au grand public pour qu'il lui serve, il l'abandonna à la naissance. »

— Johannes Kepler^[33], Rudolphine Tables, 1627

Découverte dans la deuxième moitié du XX^e siècle, la machine de Schickard n'eut aucune influence sur le développement des machines à calculer^[34].

Achèvements

En plus d'être la première machine à calculer dont la description ait été rendue publique en son temps, la Pascaline est aussi:

• la première machine à calculer utilisée dans un bureau (celui de son père pour le calcul d'impôt et la levée des tailles)
• la première machine à calculer commercialisée (avec vingt exemplaires construits^[7])
• la première machine brevetée (privilège royal de 1649^[10])
• la seule machine arithmétique décrite dans l'encyclopédie de Diderot & d'Alembert (1751):

« La première machine arithmétique qui ait paru, est de Blaise Pascal, né à Clermont en Auvergne le 19 juin 1623 ; Il l'inventa à l'âge de dix-neuf ans. On en a fait quelques autres depuis qui, au jugement même de MM. de l’Académie des Sciences, paraissent avoir sur celle de Pascal des avantages dans la pratique ; mais celle de Pascal est la plus ancienne ; elle a pu servir de modèle à toutes les autres ; c'est pourquoi nous l'avons préférée^[35]. »

• la première machine à calculer disponible chez un distributeur ( « le Sieur de Roberval ... au Collège Maître Gervais ... tous les matins jusqu'à huit heures^[36] »)
• la première machine à avoir été copiée (premier clone par un horloger de Rouen avant 1645^[36])
• la première machine à calculer à posséder un reporteur qui permettait la progression effective des retenues en cascade^[37].

Éloges littéraires

Le génie de Pascal et sa machine furent célébrés par les plus grands écrivains Français:

« Il y avait un homme qui à douze ans avec des barres et des ronds, avait créé les mathématiques ; qui à seize avait fait le plus savant traité des coniques qu'on eût vu depuis l'antiquité ; qui à dix-neuf réduisit en machine une science qui existe tout entière dans l'entendement ; qui à vingt-trois ans démontra les phénomènes de la pesanteur de l'air, et détruisit une des grandes erreurs de l'ancienne physique; ... cet effrayant génie se nommait Blaise Pascal »

— Chateaubriand, le Génie du christianisme

« Pascal, fou sublime, né un siècle trop tôt. »

— Voltaire

Dans sa lettre dédicatoire au chancelier Seguier, Pascal parle des sciences diverses qu'il utilisa pour construire sa machine: « Les lumières de la géométrie, de la physique et de la mécanique m'en fournirent le dessein »^[6]. À la suite du trois centième anniversaire de sa naissance, Léon Brunschvicg expliqua que:

« ...l'universalité de l'hommage rendu à Pascal, chez nous et dans le monde, avait sa raison dans l'unité d'un génie véritablement universel. Il arrive, en effet, que certains hommes sont doués d'un certain génie, correspondant au développement extraordinaire d'une faculté maîtresse nettement définie, à l'impérieux appel d'une vocation bien déterminée. Mais à d'autres il est donné d'incarner le génie lui-même, parce qu'ils semblent défier la théorie des facultés, planer au-dessus de toute classification. D'eux, on ne peut pas dire qu'ils sont ceci ou cela ; ils sont ceci et cela, dominant toute matière à laquelle il leur a plu de s'appliquer, y imprimant, pour la durée des temps, la trace de leur passage. A l'un des premiers rangs, dans cette famille supérieure, il y a Blaise Pascal. »

— Léon Brunschvicg, Le génie de Pascal, 1924^[38]

Pascal lui-même remarqua que:

« La machine d'arithmétique fait des effets qui approchent plus de la pensée que tout ce que font les animaux ; mais elle ne fait rien qui puisse faire dire qu'elle a de la volonté, comme les animaux. »

— Pascal, Pensées^[39]

Son génie et sa machine furent aussi célébrés par quelques poèmes d'auteurs moins connus:

Développement

Pascal décida de construire une machine à calculer pour aider son père dont l'occupation demandait beaucoup de calculs, mais qui à l'époque étaient effectués par des calculateurs (humains) avec des jetons ou à la plume. Les calculs comptables de cette époque étaient compliqués du fait que le système monétaire n’était pas décimal avec 20 sols dans une livre et 12 deniers dans un sol. Il en était de même pour le calcul de longueurs et de poids.

Les deux roues de droite sont pour les livres et les deniers

Le mécanisme complet est exposé par l'ouverture de la trappe d’accès

Machine comptable de Louis Périer

Il commença son développement en 1642 et expérimenta avec une cinquantaine de prototypes avant de s'arrêter sur le design de la première machine qu'il présentera en 1645; voici comment il décrivit son effort:

« Au reste, si quelquefois tu as exercé ton esprit à l'invention des machines, je n'aurai pas grand-peine à te persuader que la forme de l'instrument, en l'état où il est à présent, n'est pas le premier effet de l'imagination que j'ai eue sur ce sujet: j' avais commencé l'exécution de mon projet par une machine très différente de celle-ci et en sa matière et en sa forme, laquelle (bien qu'en état de satisfaire à plusieurs) ne me donna pas pourtant la satisfaction entière; ce qui fit qu'en la corrigeant peu à peu j'en fis insensiblement une seconde, en laquelle rencontrant encore des inconvénients que je ne pus souffrir, pour y apporter le remède, j'en composai une troisième qui va par ressorts et qui est très simple en sa construction. C'est celle de laquelle, comme j'ai déjà dit, je me suis servi plusieurs fois, au vu et su d'une infinité de personnes, et qui est encore en état de servir autant que jamais. Toutefois, en la perfectionnant toujours, je trouvai des raisons de la changer, et enfin reconnaissant dans toutes, ou de la difficulté d'agir, ou de la rudesse aux mouvements, ou de la disposition à se corrompre trop facilement par le temps ou par le transport, j'ai pris la patience de faire jusqu'à plus de cinquante modèles, tous différents, les uns de bois, les autres d'ivoire et d'ébène, et les autres de cuivre, avant que d'être venu à l'accomplissement de la machine que maintenant je fais paraître; laquelle, bien que composée de tant de petites pièces différentes, comme tu pourras voir, est toutefois tellement solide, qu'après l'expérience dont j'ai parle ci-devant, j'ose te donner assurance que tous les efforts qu'elle pourrait recevoir en la transportant si loin que tu voudras, ne sauraient la corrompre ni lui faire souffrir la moindre altération^[36]. »

Cette invention le rendit immédiatement célèbre.

Applications

La roue pascaline comptait dans le système décimal le nombre d'unité d'un ensemble de mesures non-décimales de l'ancien régime. Pour cela il fallait des machines avec des roues de:

• 6 dents pour les pieds (6 pieds dans une toise)
• 10 dents pour les livres et les toises et pour le système décimal/scientifique
• 12 dents pour les deniers (12 deniers dans un sol), les pouces (12 pouces dans un pied) et les lignes (12 lignes dans un pouce)
• 20 dents pour les sols (20 sols dans une livre)

Quatre Pascalines de différentes capacités et un clone de Lépine, au Musée des arts et métiers à Paris

Trois types de machines nous sont parvenues: scientifiques, comptables et géomètres.

Machines connues et recensées

D'une vingtaine de machines produites, il n'en subsiste que neuf :

Échec commercial

La commercialisation de la pascaline fut un échec principalement à cause de son prix élevé qui était de 100 à 400 livres mais le texte du privilège royal de 1649 montre que Pascal était en train de développer une machine à calculer plus simple :

« Et parce que ledit instrument est maintenant à un prix excessif qui le rend, par sa cherté, comme inutile au public, et qu'il espère le réduire à moindre prix et tel qu'il puisse avoir cours, ce qu'il prétend faire par l'invention d'un mouvement plus simple et qui opère néanmoins le même effet, à la recherche duquel il travaille continuellement, et en y stylant peu a peu les ouvriers encore peu habitués^[10]... »

Pascal voulait donc simplifier sa machine et la rendre plus accessible au grand public mais un accident de carrosse malencontreux, en octobre 1654, le fit se retirer du monde scientifique et se consacrer uniquement à la poursuite de la philosophie et de la religion. L'accident arriva quand deux des quatre chevaux de son carrosse tombèrent dans la Seine sur le pont de Neuilly ; alors,

« ...il eut beaucoup de peine à revenir d'un long évanouissement ; son cerveau fut tellement ébranlé, que dans la suite, au milieu de ses insomnies et de ses exténuations, il croyait voir de temps en temps, à côté de son lit, un précipice prêt à l'engloutir^[44]. »

Cet échec commercial vient aussi du fait que (en parlant des machines de Pascal et de Leibniz en 1779):

« ...ces machines sont coûteuses, un peu embarrassantes par le volume, et sujettes à se déranger. Ces inconvénients font plus que compenser leur avantages. Aussi les Mathématiciens préfèrent-ils généralement les tables des logarithmes, qui changent les opérations les plus compliquées de l’arithmétique en de simples additions ou soustractions, auxquelles il suffit d'apporter une légère attention, pour éviter les erreurs de calcul^[45]. »

Il semble aussi qu'au siècle de Pascal les gens n’avaient pas l'habitude d'utiliser des machines, comme cette mise en garde le montre:

« Il est bon d'avertir que lorsqu'on remarque ainsi qu'en opérant sur une roue, les autres roues changent de chiffre, il ne faut pas s'imaginer qu'il y ait du désordre dans la machine car au contraire^[46]... »

Composants

Planche montrant la platine de la Pascaline et l'ensemble de son mécanisme

Planche détaillant le mécanisme complet d'une roue ainsi que le sautoir

Œuvres de Pascal en 5 volumes, La Haye, 1779

La platine

Vue d'ensemble

Roue d'inscription
Deux poinçons sur deux rayons consécutifs (en haut à droite) marquent l'emplacement de remise à zéro pour cette roue.
Il y a une rondelle de soustraction mais les chiffres sont à peine visibles.

La platine a deux parties bien distinctes: la partie basse qui permet l'entrée des données et qui est composée de roues d'inscriptions qui ressemblent aux cadrans téléphoniques du milieu du XX^e siècle, et la partie haute, composée d'un ensemble de lucarnes, qui servent à l’affichage des résultats. Chaque lucarne de résultat présente deux chiffres. Ils sont positionnés au-dessus l'un de l'autre et sont complémentaires dans la base choisie ; une barre horizontale, coulissante, masque une ligne à la fois, montrant ainsi soit tous les nombres directs quand elle est le plus près du bord de la machine, soit tous leurs compléments quand elle est positionnée vers le centre de la machine. Chaque lucarne de résultat est directement associée à une roue d'inscription.

Roue d'inscription

Pour une roue de 10 chiffres, l’extérieur fixe est numéroté, dans le sens des aiguilles d'une montre, à partir du butoir, avec une suite de nombres d'ordre décroissant de 9 à 0. Une roue étoilée mobile à 10 rayons est positionnée à l’intérieur de ce cadran. Pour ajouter 5 il suffit de positionner la pointe d'un stylet entre les rayons qui encadrent le chiffre 5 et de tourner la roue, dans le sens des aiguilles d'une montre, jusqu'au butoir.

Rayons contigus marqués

Sur toutes les machines^[47], les roues ont des marques sur deux rayons consécutifs de la roue étoilée. Le type de marque dépend de la machine (ce sont deux poinçons sur la photo de droite)^[48]. En positionnant le stylet entre ces deux rayons et en tournant jusqu'au butoir, la roue concernée est mise à son maximum (5, 9, 11, 19), prête à être remise à zéro. En effet la roue étoilée est solidaire de son cylindre d'affichage (c'est pourquoi elle tourne d'un cran pendant un report de retenue) et donc chaque position de la roue correspond à un nombre sur son cylindre. Pour inscrire ces rayons pendant la fabrication d'une machine il suffit d'amener le cylindre à son maximum et de marquer le rayon en dessous du butoir et celui immédiatement à sa droite.

Ces deux rayons marqués peuvent aussi être utilisés pour entrer le premier nombre d'une soustraction dans la fenêtre des compléments. L’opérateur doit inscrire les chiffres de droite à gauche ; pour chaque chiffre dans le nombre, il suffit d’encadrer sa représentation sur la jante fixe avec ces deux rayons sans oublier de le faire aussi pour les zéros d'ordre supérieur. Si l'on procède ainsi, il n'est pas nécessaire de remettre la machine à zéro préalablement.

Les rondelles de mémoire

Quatre des neuf machines recensées possèdent des rondelles de mémoires montées sur la barre horizontale coulissante. Elles sont appelées roues de quotient ou cercles de quotient et sont utilisées par l’opérateur pour mémoriser les quotients dans une division^[49].

Les rondelles concentriques de soustraction

Quatre machines possèdent des rondelles concentriques de soustraction^[50]. Ces rondelles sont solidaires des roues étoilées qui les supportent, elles sont placées en leurs centres et tournent avec elles. Il suffit de positionner la pointe d'un stylet entre les rayons qui encadrent un chiffre gravé sur ces rondelles et de tourner dans le sens des aiguilles d'une montre jusqu'au butoir pour inscrire ce chiffre directement dans la fenêtre de soustraction. Les deux rayons contigus encadrent le chiffre 0 de la rondelle de soustraction.

Le sautoir

Le sautoir
Le cliquet (en rouge) avec son ressort (en jaune) qui le pousse contre une des chevilles de la roue suivante.
(détail d'une planche de 1779 coloriée)

Principe de fonctionnement

Pascal disait à propos du sautoir:

« ...pour la facilité de ce ... mouvement .... il est aussi facile de faire mouvoir mille et dix mille roues tout à la fois, si elles y étaient, quoique toutes achèvent leur mouvement très parfait, que d'en faire mouvoir une seule (je ne sais si, après le principe sur lequel j'ai fondé cette facilité, il en reste un autre dans la nature)^[36]... »

Une machine à dix mille roues marcherait aussi bien qu'une machine à deux roues car chaque roue d’entrée est totalement indépendante des autres. Quand il est temps de transmettre l'information de retenue, la roue concernée envoie son sautoir vers la roue suivante sans qu'il y est de contact entre les deux roues. En tombant de son seul poids^[51], le sautoir se lance vers la roue suivante comme un acrobate qui se jette d'un trapèze à un autre sans que les trapèzes se touchent. Toutes les roues (avec engrenages et sautoir) sont ainsi identiques en poids et en taille quel que soit le nombre de roues.

Pascal utilisa la gravité pour armer ses sautoirs. Il faut tourner une roue de cinq crans pour armer le sautoir totalement (il est engagé quand le chiffre du cadran est à 4 et monte progressivement jusqu'à 9) en revanche, quand il transmet la retenue, le sautoir ne doit faire tourner la roue suivante que d'un cran. Le sautoir a donc un surplus d’énergie important, ce qui permet au système de retenue de ne jamais se bloquer.

Tous les sautoirs sont armés par l'entré des données et par les retenues des roues précédentes. Pour remettre à zéro une machine de dix mille chiffres, si elle existait, il faudrait amener chacun des dix mille cadrans à neuf (ce qui armerait tous les sautoirs) et puis ajouter un 1 à la roue des unités. La propagation des retenues ressemblerait alors à un effet domino très rapide.

Les trois phases de progression de retenue

Les trois temps de l'utilisation du sautoir.
(détail d'une planche de 1779 coloriée)

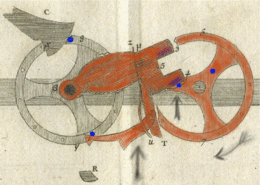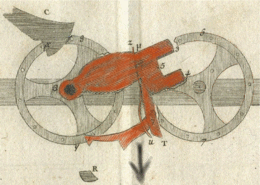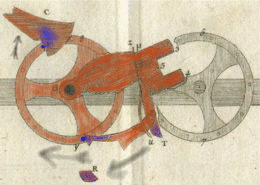
L'image de droite montre les trois différentes phases de progression de retenue.

1. Pour une roue décimale, c'est pendant que le résultat affiché va de 4 à 9 que, l'une après l'autre, les deux chevilles de retenue lèvent le sautoir en le poussant sur sa partie échancrée (3,4,5). Pendant ce temps, le cliquet (1) est poussé contre une des chevilles de la roue de retenue grâce à son ressort (z,u) mais il n'a aucun effet sur cette roue car le cliquet supérieur (C) l'en empêche.
2. La retenue se transmet quand le cadran d'affichage va de 9 à 0. En premier lieu, le cliquet (1) dépasse la cheville sur laquelle il était appuyé et son ressort le pousse au-dessus de celle-là prêt à la pousser quand il retombera ; le sautoir continue de monter puis, un instant plus tard, la deuxième cheville de retenue le laisse tomber. Le sautoir est maintenant en chute libre^[52].
3. Le cliquet (1) rentre en contact avec la cheville de la roue de retenue et la pousse sous l'action de la pesanteur. La roue tourne et le cliquet supérieur (C) se cale entre les deux chevilles suivantes. Le tout s’arrête quand la partie (T) du sautoir rentre en contact avec le butoir (R).

Compétition

Il fallut attendre trois siècles pour voir ce mécanisme amélioré avec le comptomètre A de Dorr E. Felt. Felt utilisa des ressorts pour armer ses retenues et comme avec la pascaline plus le nombre affiché est haut plus le ressort est armé près à délivrer sa retenue à l'ordre suivant^[53].

Notices d'utilisation

Pascal pensait qu'une notice d'utilisation n'était pas nécessaire:

« ...tu jugeras que cette doctrine est du nombre de celles qui ne peuvent être enseignées que de vive voix, et qu'un discours par écrit en cette matière serait autant et plus inutile et embarrassant que celui qu'on emploierait à la description de toutes les parties d'une montre, dont toutefois l'explication est si facile, quand elle est faite bouche à bouche^[36]... »

Il y a une exception décrite dans la Lettre à la Sérénissime Reine de Suède (juin 1652), qu'il écrivit quand il lui fit don d'une de ses machines. Cette lettre dit que M. de Bourdelot, la personne chargée de délivrer cette machine, avait aussi en sa possession un discours qui expliquait:

« ...toute l'histoire de cet ouvrage, l'objet de son invention, l'occasion de sa recherche, l'utilité de ses ressorts, les difficultés de son exécution, les degrés de son progrès, le succès de son accomplissement et les règles de son usage^[54]. »

Ce discours, qui serait le seul manuel d’utilisation écrit par Pascal, n'a jamais été retrouvé.

En 1982, la municipalité de Clermont-Ferrand fit l'acquisition de la copie d'une notice d'utilisation exécutée au XVIII^e siècle et dont l'auteur pourrait être Etienne Périer^[55]. Cette copie intitulée Usage de la machine fut publiée en 1986 dans le numéro 8 du Courrier du centre international Blaise Pascal de Clermont-Ferrand.

Les opérations

Principe

On ne peut effectuer directement que des additions et des soustractions. Les soustractions utilisent le principe du complément à 9 et sont donc entièrement effectuées dans la fenêtre des compléments.

Rien n'empêche de faire des multiplications par additions successives, ni des divisions par soustractions successives. Ce que nous trouverions un peu fastidieux devait être jugé très commode à l'époque de Pascal. Des rondelles de mémoire, présentent sur certaines machines, permettent de conserver des résultats intermédiaires.

Complément à 9

Dans une machine décimale à n chiffres, le complément à 9 ou complément pascalien^[56] d'un nombre A vaut:

CP(A)= 10ⁿ - 1 - A

et donc le complément à 9 de (A - B) vaut:

CP(A - B)= 10ⁿ -1 - (A - B) = 10ⁿ -1 - A + B = CP(A) + B

Ceci appliqué à la pascaline:

CP(A):      le premier chiffre doit être entré dans la fenêtre des compléments en utilisant les rondelles concentriques de soustraction.

B:             puis le deuxième chiffre est entré comme pour une addition.

CP(A - B): le résultat est présent dans la fenêtre des compléments.

Le même principe est valable et peut être utilisé avec les pascalines non décimales (comptable et géomètre).

Remise à zéro de la machine

Ceci ce fait en utilisant les rayons contigus marqués. Pour chaque roue de la machine, il faut positionner le stylet entre ces deux rayons et tourner jusqu'au butoir. Ceci peut ce faire dans n’importe quel ordre mais doit être fait sur tous les cadrans^[57]. Puis il faut ajouter un au chiffre des unités^[30]. Si la barre horizontale est en position d'addition, toutes les roues se remettent à zéro et si elle est en position de soustraction, chacune est mise à son maximum. Dans les deux cas, les rayons contigus marqués encadrent le chiffre maximum de chaque roue d'inscription.

Il faut remarquer que la remise à zéro, nécessaire avant chaque nouvelle opération, prouve que la machine fonctionne parfaitement, car elle force le report de retenue sur toutes les roues.

Addition

La barre horizontale doit être placée près du bord de la machine en position d'addition. Après avoir mit la machine à zéro, il suffit d'inscrire les nombres les uns après les autres en utilisant les roues étoilées et le stylet. C'est un mode d'inscription direct et donc les retenues se font durant l'inscription des nombres^[58].

Soustraction

La barre horizontale doit être placée près du centre de la machine en position de soustraction et donc expose le complément des nombres inscrits. Une remise à zéro de la machine fait apparaître le chiffre maximum sur chaque roue de la forme 99999xxx, x étant un des chiffres 5, 9, 11 ou 19 et dépend du type de machine utilisée (comptable, scientifique, géomètre). Il y a trois méthodes pour inscrire le premier nombre^[59]:

• Si la machine a des rondelles concentriques de soustraction, pour chaque chiffre dans le nombre, il suffit de le trouver sur sa rondelle de soustraction, de positionner la pointe d'un stylet entre les rayons qui l’entourent et de tourner la roue étoilée dans le sens des aiguilles d'une montre jusqu'au butoir.
• Une autre méthode, aussi simple, est d'utiliser les rayons contigus marqués et, pour chaque chiffre dans le nombre, il suffit de tourner la roue étoilée dans le sens des aiguilles d'une montre et de s’arrêter quand ces rayons contigus marqués l'encadrent. Il est a noté qu’après une remise à zéro, et sur toutes les roues, les rayons contigus marqués encadrent le chiffre maximum (5, 9, 11, 19) de la jante fixe.
• L’opérateur peut aussi utiliser le complément de ce nombre et l'inscrire comme pour une addition. Par exemple, pour faire apparaître 710 dans la fenêtre des compléments d'une machine décimale, il suffit d'inscrire 289 avec les roues étoilées.

Une fois le nombre inscrit, l’opérateur peut soit mettre les chiffres d'ordres supérieurs à zéro, soit les garder à leurs maximum à condition de ne pas les considérer dans le résultat de la soustraction suivante.

Grâce au complément à 9, il suffit d'inscrire le nombre à soustraire comme pour une addition et le résultat se trouve immédiatement dans la fenêtre de soustraction. L’opérateur peut soustraire autant de nombres qu'il veut tant que le nombre à soustraire est plus petit que le résultat de l’opération précédente.

Les rondelles de mémoire peuvent être utilisées pour mémoriser le résultat d'une soustraction si ce nombre est à utiliser dans une addition suivante.

Par la suite

En 1673, Leibniz invente une machine capable d'effectuer plus simplement multiplications et divisions, grâce à un système de cylindres à dents de longueurs inégales, dits cylindres de Leibniz, servant de « mémoire ».

Calculatrice mécanique hexadécimale IBM

Certains disent que la Pascaline connut une période de gloire dans les années 1960 en usage interne dans la compagnie IBM, qui en aurait fait fabriquer. C'était alors en effet le seul dispositif bon marché permettant d’effectuer très vite des calculs en numération hexadécimale, comme le demandait la programmation de l’époque. Cette rumeur repose en fait sur la rencontre de deux événements indépendants :

1. la commande par IBM, auprès d'un artisan de New-York, d'une centaine de reproductions exactes de la Pascaline de leur collection, qui ont été offertes à leurs meilleurs clients, et que l'on trouve aujourd'hui parfois en vente sur le marché de l'antiquité.
2. la réalisation d'une petite machine mécanique de poche, en plastique, basée sur le principe de la Pascaline, et possédant 4 roues de 16 chiffres pour calculer en hexadécimal (voir photo).

Notes

Sources

• « Usage de la machine », dans Courrier du centre international Blaise Pascal, Clermont-Ferrand, n^o 8, 1986 
• Blaise Pascal 1623-1662, Paris, Bibliothèque Nationale, 1962 
• Pierre Humbert, Cet effrayant Génie... L'Oeuvre scientifique de Blaise Pascal, Paris, Albin Michel, 1947 
• Blaise Pascal, Pensées de Pascal, précédées de Sa vie, par M^me Périer, sa sœur, Paris, Librairie de Firmin-Didot frères, fils & Cie, 1873 
• Blaise Pascal, Oeuvres de Blaise Pascal, t. 1, Chez Detune, La Haye, 1779 
• Blaise Pascal, Oeuvres de Blaise Pascal, t. 4, Chez Detune, La Haye, 1779 
• Michel Collin, La machine à calculer de Blaise Pascal, Nathan, Paris, 1993 
• Guy Mourlevat, Les machines arithmétiques de Blaise Pascal, La Française d'Edition et d'Imprimerie, Clermont-Ferrand, 1988 
• Jean Marguin, Histoire des instruments et machines à calculer, trois siècles de mécanique pensante 1642-1942, Hermann, 1994 (ISBN 978-2-7056-6166-3) 
• René Taton, Le calcul mécanique. Que sais-je ? n° 367, Presses universitaires de France, 1949 
• René Taton, Le calcul mécanique. Que sais-je ? n° 367, Presses universitaires de France, 1963, p. 20-28 
• René Taton, Histoire du calcul. Que sais-je ? n° 198, Presses universitaires de France, 1969 
• Collectif, Catalogue du musée - Section A Instruments et machines à calculer, Conservatoire National des Arts et Métiers, Paris, 1942 
• Maurice d'Ocagne, Annales du Conservatoire national des arts et métier, 2e série, tome 5 : Le calcul simplifié, Paris, Gauthiers-Villars et files, Imprimeurs-Libraires, 1893 [lire en ligne] 
• Georges Ifrah, Histoire universelle des chiffres, Paris, Éditions Seghers, 1981 (ISBN 2-221-50205-1) 
• Léon Brunschvicg, Le génie de Pascal, Paris, Librairie Hachette, 1924 

• (en) S. Chapman, « Blaise Pascal (1623-1662): Tercentury of the Calculating Machine », dans Nature, vol. 150, n^o 3809, 31 octobre 1942 
• (en) Georges Ifrah, The Universal History of Numbers, vol. 3 : The Computer and the Information Revolution, London, The Harvill Press, 2000 (ISBN 978-1-86046-738-7) 
• (en) Dorr E. Felt, Mechanical arithmetic, or The history of the counting machine, Chicago, Washington Institute, 1916 [lire en ligne] 
• (en) Jekuthiel Ginsburg, Scripta Mathematica (Septembre 1932-Juin 1933), Kessinger Publishing, LLC, 2003 (ISBN 978-0-7661-3835-3) 
• (en) Joseph Needham, Science and Civilization in China: Volume 4, Physics and Physical Technology, Part 2, Mechanical Engineering, Taipei, Caves Books, Ltd., 1986 
• (en) J. A. V. Turck, Origin of modern calculating machines, Chicago, The western society of engineers, 1921 
• (en) Michael R. Williams, History of Computing Technology, Los Alamitos, California, IEEE Computer Society, 1997 (ISBN 0-8186-7739-2) 
• (en) Mark Napier, Memoirs of John Napier of Merchiston, Edinburgh, William Blackwood, 1834 [lire en ligne] 
• (en) Stan Augarten, Bit by Bit, An illustrated history of Computers, New York, New York, Ticknor & Fields, 1984 (ISBN 0-89919-268-8) 
• (en) Eric G. Swedin, David L. Ferro, Computers: The Life Story of a Technology, Greenwood, 2005 (ISBN 978-0313331497) 

Liens externes

• La Pascaline, détaillée par un chercheur
• Le texte de B. Pascal sur sa machine, en ligne et commenté sur le site Bibnum: la Pascaline. (page consultée le 29-11-2010)
• Copie d'un livre sur des reproductions de la Pascaline. (page consultée le 29-11-2010)
• (de) Staatlichen Kunstsammlungen Dresden - Mathematisch-Physikalischer Salon Musée de Dresde - Section des Mathématiques et de la Physique. (page consultée le 29-11-2010)

• Portail de l’informatique