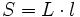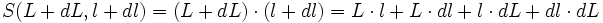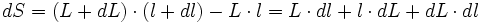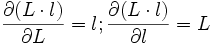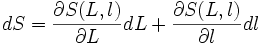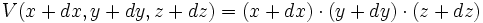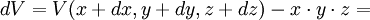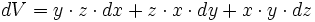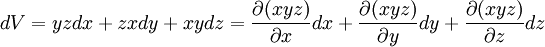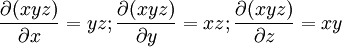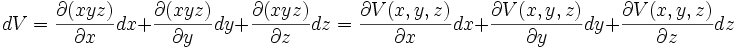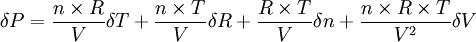Calcul d'incertitudes

Calcul d'incertitude

Le calcul d'incertitude permet d'évaluer correctement les erreurs qui se produisent lors de mesures liées à la vérification d'une relation entre différentes grandeurs physiques. Les instruments de mesure n'étant pas de précision infinie, les mesures faites pendant une expérience ne sont pas exactes. Il faut donc évaluer ces incertitudes pour répondre à la question : « la relation n'est pas vérifiée exactement parce qu'elle est fausse ou parce que les mesures sont incertaines ? » On en déduit des marges d'erreurs, en dehors desquelles la relation sera invalidée. Cela fait partie intégrante de la méthode scientifique.

Sommaire

1 Méthodes de base
- 1.1 Incertitude sur une somme ou une différence
- 1.2 Incertitude sur un produit ou un rapport
2 Utilisation des différentielles totales exactes
3 Utilisation de calculatrices
4 Références
5 Références externes

Méthodes de base

Le calcul des incertitudes, à ne pas confondre avec l'erreur, sur des grandeurs dérivées des grandeurs mesurées pour lesquelles il est possible d'estimer les erreurs $Δ x$ peut être présenté simplement et sans démonstration comme ci-dessous. Une démonstration plus précise et rigoureuse nécessite l'usage du calcul différentiel, typiquement au programme des lycées en France et de la fin du secondaire en Belgique.

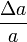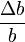
Soit les grandeurs mesurées $a$ et $b$ avec leurs incertitudes absolues $Δ a$ et $Δ b$ , et leurs incertitudes relatives $\frac{\Delta a}{a}$ et $\frac{\Delta b}{b}$

Incertitude sur une somme ou une différence

Si $c = a + b$ , $Δ c = Δ a + Δ b$ , et

Si $c = a - b$ , $Δ c = Δ a + Δ b$ aussi.

Autrement dit, l'incertitude absolue sur la somme ou la différence de 2 grandeurs est égale à la somme des incertitudes absolues de ces grandeurs.

Incertitude sur un produit ou un rapport

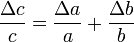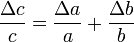Si $c = a * b$ , $\frac{\Delta c}{c} = \frac{\Delta a}{a} + \frac{\Delta b}{b}$ , et

Si $c = a / b$ , $\frac{\Delta c}{c} = \frac{\Delta a}{a} + \frac{\Delta b}{b}$ aussi.

Autrement dit, l'incertitude relative sur un produit ou un rapport de 2 grandeurs est égale à la somme des incertitudes relatives de ces grandeurs.

Utilisation des différentielles totales exactes

Une loi physique s'exprime par une relation algébrique entre un certain nombre de grandeurs mesurables.

Exemples simples : surface et volume

Le calcul de la surface d'un rectangle de côtés L et l :

$S=L \cdot l$

devient lorsque les côtés deviennent L+dL et l+dl:

$S(L+dL,l+dl) = (L+dL) \cdot(l+dl) = L\cdot l + L \cdot dl +l\cdot dL + dl\cdot dL$

Donc la variation de la surface dS peut s'écrire :

$dS = (L+dL)\cdot (l+dl) - L \cdot l = L\cdot dl +l\cdot dL + dL\cdot dl$

que l'on approche par :

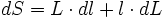$dS = L\cdot dl +l\cdot dL$ car dL.dl est négligeable.

Noter que

$\frac{\partial (L\cdot l) }{\partial L}= l ; \frac{\partial (L\cdot l) }{\partial l}=L$

d'où

$dS = \frac{\partial S(L,l) }{\partial L}dL+\frac{\partial S(L,l) }{\partial l}dl$

De même la variation de volume d'une boîte de côtés x, y, z de volume V=xyz :

$V(x+dx,y+dy,z+dz) = (x+dx)\cdot(y+dy)\cdot(z+dz)$

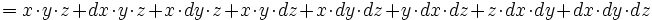
$= x\cdot y\cdot z +dx\cdot y \cdot z+x\cdot dy\cdot z + x\cdot y\cdot dz + x\cdot dy\cdot dz + y\cdot dx\cdot dz + z\cdot dx\cdot dy + dx\cdot dy\cdot dz$

peut s'écrire

$dV =V(x+dx,y+dy,z+dz) - x\cdot y\cdot z =$

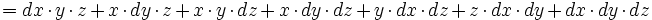
$= dx\cdot y \cdot z+x\cdot dy\cdot z + x\cdot y\cdot dz + x\cdot dy\cdot dz + y\cdot dx\cdot dz + z\cdot dx\cdot dy + dx\cdot dy\cdot dz$

que l'on approche par :

$dV = y\cdot z\cdot dx +z\cdot x\cdot dy + x\cdot y\cdot dz$

Noter que :

$dV = yz dx +zx dy + xy dz = \frac{\partial (xyz) }{\partial x}dx+\frac{\partial (xyz) }{\partial y}dy+\frac{\partial (xyz) }{\partial z}dz$

car

$\frac{\partial (xyz) }{\partial x}= yz ; \frac{\partial (xyz) }{\partial y}=xz ; \frac{\partial (xyz) }{\partial z}=xy$

et donc

$dV = \frac{\partial (xyz) }{\partial x}dx+\frac{\partial (xyz) }{\partial y}dy+\frac{\partial (xyz) }{\partial z}dz= \frac{\partial V(x,y,z) }{\partial x}dx+\frac{\partial V(x,y,z) }{\partial y}dy+\frac{\partial V(x,y,z) }{\partial z}dz$

La variation d'une fonction f(x,y,z)

Et plus généralement, pour le calcul de la variation d'une fonction f(x,y,z).

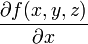$\frac{\partial f(x,y,z) }{\partial x}$ = dérivée partielle par rapport à x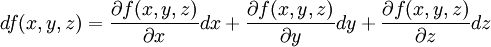

$d f(x,y,z) = \frac{\partial f(x,y,z) }{\partial x}dx+\frac{\partial f(x,y,z) }{\partial y}dy+\frac{\partial f(x,y,z)}{\partial z}dz$

Loi des gaz parfaits

Prenons par exemple la loi des gaz parfaits reliant :

P : la pression du gaz
V : le volume occupé par le gaz
n : la quantité de gaz en moles (1 mole = 6,022 10²³ molécules)
R : la constante des gaz parfaits = 8,314 J.K^-1.mol^-1
T : la température absolue du gaz, en kelvin.

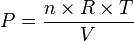$P =\frac{n \times R \times T}{V}$ exprime la pression en fonction de n, R, T et V.

Écrivons sa différentielle :

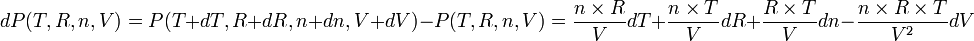$dP (T,R,n,V)=P (T+dT,R+dR,n+dn,V+dV)-P (T,R,n,V) = \frac{n \times R}{V} dT + \frac{n \times T}{V} dR + \frac{ R \times T}{V}dn - \frac{n \times R \times T}{V^2}dV$ .

la variation la plus grande s'obtiendra lorsque les 4 termes ci-dessus s'ajouteront :

$\delta P =\frac{n \times R}{V}\delta T + \frac{n \times T}{V}\delta R +\frac{ R \times T}{V}\delta n + \frac{n \times R \times T}{V^2}\delta V$

donne l'erreur absolue sur P déduite du calcul de P à partir de la connaissance des erreurs sur T, R, n et V.

Dans ce cas particulier, on a :

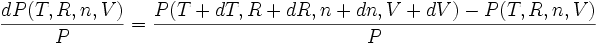$\frac{dP (T,R,n,V)}{P} = \frac{P (T+dT,R+dR,n+dn,V+dV)-P (T,R,n,V)}{P}$ .

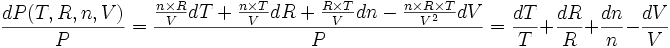$\frac{dP (T,R,n,V)}{P} = \frac{ \frac{n \times R}{V} dT + \frac{n \times T}{V} dR +\frac{ R \times T}{V} dn - \frac{n \times R \times T}{V^2} dV }{P}= \frac{dT}{T} + \frac{dR}{R} +\frac{dn}{n} - \frac{dV}{V}$ .

et donc dans l'absolu :

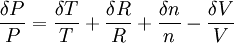$\frac{\delta P}{P} =\frac{\delta T}{T} + \frac{\delta R}{R} +\frac{\delta n}{n} - \frac{\delta V}{V}$ .

On peut aussi utiliser la différentielle logarithmique :

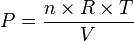$P =\frac{n \times R \times T}{V}$ .

Donc

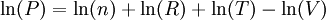$\ln(P) =\ln(n) +\ln(R) +\ln(T) -\ln(V)\,$ .

En dérivant, on obtient :

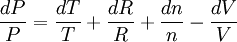$\frac{dP}{P} =\frac{dT}{T} + \frac{dR}{R} +\frac{dn}{n} - \frac{dV}{V}$ .

Cette méthode plus rapide s'applique lorsqu'on cherche à faire la différentielle d'une fonction, quotient ou produit de plusieurs variables.

Les incertitudes relatives s'ajoutent lorsque l'on a un produit de variables et ce résultat est remarquable car il est facile à retenir : les incertitudes relatives s'ajoutent lorsque la formule ne comporte que des produits (au sens large : une division est un produit par l'inverse).

Utilisation de calculatrices

Ce qui vient d'être fait peut être fait par calcul direct avec une calculatrice ou un tableur (sur ordinateur):

Utilisation de graphes et de barres d'erreurs

Reprenons l'exemple de l'étude des gaz parfaits. Si l'on trace P en fonction de 1/V, on obtiendra théoriquement une droite passant par l'origine 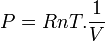$P = R n T . \frac{1}{V}$ , avec comme pente $R n T$ , soit $y = (R n T). x$ , n et T étant maintenus constants (l'enceinte ou cellule de mesure contenant le gaz étant sans fuite et thermostatée avec T connu à 0,2%), P étant mesuré, en utilisant un manomètre, avec 5% d'erreur relative, et V étant mesuré avec 2% d'erreur relative, pour chaque point de mesure expérimentale (P,1/V), on trace des barres d'erreurs représentant l'erreur absolue.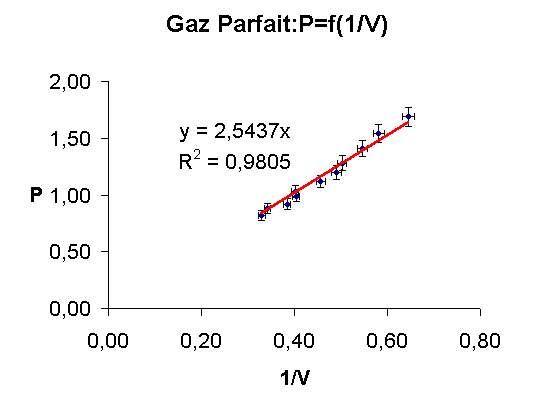

PV=nRT.jpg

Un programme de « fit » ou d'ajustage de courbe, basé sur l'idée de minorer la distance de la droite (ou courbe) à tous les points expérimentaux, permet de tracer la droite théorique et de calculer sa pente nRT avec un coefficient de confiance r² proche de l'unité, si le fit est bon. On utilise la "méthode des moindres carrés" : le programme utilisé somme les distances entre la droite et chaque point, le minimum de cette somme correspondant à la meilleure droite de régression.

Dans le cas de figure ci dessus, on obtient ainsi nRT= 2.54 (1 ± 0.07) Joule

Ceci permet de dire que à n et T constants, l'expérience confirme que PV est constant à 7% près pour le gaz étudié et que pour améliorer ce résultat, il faut mesurer P à mieux que 5% ou V à mieux que 2%.

Références

Propagation des erreurs

Références externes

Ten Theses for a New GUM

Portail de la physique

Ce document provient de « Calcul d%27incertitude ».

Catégorie : Statistiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Calcul d'incertitudes de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Calcul D'incertitude — Le calcul d incertitude permet d évaluer correctement les erreurs qui se produisent lors de mesures liées à la vérification d une relation entre différentes grandeurs physiques. Les instruments de mesure n étant pas de précision infinie, les… … Wikipédia en Français
Calcul d'erreur — Erreur (métrologie) Pour les articles homonymes, voir Erreur et Incertitude. Le calcul d erreur, ou calcul d incertitudes est un ensemble de techniques permettant d estimer l erreur faite sur un résultat numérique, à partir des incertitudes ou… … Wikipédia en Français
Calcul d'incertitude — Le calcul d incertitude permet d évaluer correctement les erreurs qui se produisent lors de mesures liées à la vérification d une relation entre différentes grandeurs physiques. Les instruments de mesure n étant pas de précision infinie, les… … Wikipédia en Français
Calcul économique — Microéconomie La microéconomie (ou micro économie) est la branche de l économie qui analyse le comportement économique au niveau d entités individuelles telles qu un consommateur ou une entreprise. Les consommateurs sont considérés comme des… … Wikipédia en Français
Propagation des incertitudes — Une mesure est toujours entachée d erreurs dont on estime l intensité par l intermédiaire des incertitudes. Lorsqu une mesure est utilisée pour obtenir la valeur d une autre grandeur par l intermédiaire une formule, outre le calcul de la valeur… … Wikipédia en Français
Determination des constantes d'equilibre — Détermination des constantes d équilibre Les constantes d équilibre sont évaluées pour quantifier les équilibres chimiques à partir de mesures de concentrations, directes ou indirectes, et mettant en œuvre des techniques numériques. Cet article… … Wikipédia en Français
Détermination des constantes d'équilibre — Les constantes d équilibre sont évaluées pour quantifier les équilibres chimiques à partir de mesures de concentrations, directes ou indirectes, et mettant en œuvre des techniques numériques. Cet article se limite aux équilibres en solutions… … Wikipédia en Français
Incertitude Absolue — En physique, l incertitude absolue Δg est l incertitude en valeur absolue sur la valeur g d une grandeur physique. Elle a la même dimension que la grandeur physique. Elle s oppose à l incertitude relative Δg/g qui est sans dimension et s exprime… … Wikipédia en Français
Incertitude absolue — Pour les articles homonymes, voir Absolu. En physique, l incertitude absolue Δg est l incertitude en valeur absolue sur la valeur g d une grandeur physique. Elle a la même dimension que la grandeur physique. Elle s oppose à l incertitude relative … Wikipédia en Français
Erreur (Métrologie) — Pour les articles homonymes, voir Erreur et Incertitude. Le calcul d erreur, ou calcul d incertitudes est un ensemble de techniques permettant d estimer l erreur faite sur un résultat numérique, à partir des incertitudes ou des erreurs faites sur … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Calcul d'incertitudes