Groupe de diviseurs

Diviseur (géométrie algébrique)

Les Diviseurs de Weil et de Cartier sont des outils de la géométrie algébrique.

En géométrie algébrique, comme en analyse complexe, ou en géométrie arithmétique, les diviseurs forment un groupe qui permet de saisir la nature d'un schéma (une variété algébrique, une surface de Riemann, un anneau de Dedekind...) au travers d'un squelette assez simple. Ce groupe provient de l'idée commune aux études menées sur ces objets : on peut connaître une grande part de leur géométrie en étudiant les sous-schémas non triviaux maximaux (sous variétés, ou idéaux de codimension 1).

L'ensemble de ces diviseurs est muni d'une loi de groupe additive. Plusieurs définitions sont possibles, selon le cadre dans lequel on agit. Néanmoins, sous de bonnes conditions, les diviseurs qu'on obtient sont identiques.

On peut agir ainsi dans le cadre de variétés définies sur un corps algébriquement clos ( 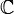$\C$ par exemple) ou sur un corps de nombre quelconque (voire 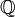$\Q$ ou les corps p-adiques). On peut les définir sur des structures souples (par exemple des changements de cartes holomorphes) ou plus rigides (variétés algébriques). On peut se placer localement (sur un anneau) ou plus globalement, en regardant toute une surface (et donner alors leur définition à l'aide de faisceau). On peut encore définir les variétés sur lesquelles on veut travailler en termes de schémas, on obtient alors une définition cohomolgique des groupes de diviseurs.

Par bonheur, les deux formes fondamentales de diviseurs : ceux de Weil et ceux de Cartier coïncident assez souvent.

Sommaire

1 Diviseurs de Weil dans une variété.
2 Diviseurs de Cartier d'une variété irréductible.
3 Diviseurs remarquables.
4 Le langage des Anneaux.
5 Sources Web
6 Bibliographie

Diviseurs de Weil dans une variété.

Variétés projectives propres et lisses.

Les variétés algébriques sur lesquelles on agit généralement sont définies par des combinaisons booléennes d'égalités de polynômes dans l'espace projectif $P n (k)$ . Immergée dans un espace projectif, on suppose que c'en est un fermé, c'est à dire une variété elle même projective. Affirmer qu'elle est propre, dans le cas où l'on se place sur 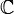$\C$ (ou l'un de ses sous-corps) revient à dire que l'ensemble de ses points complexes est compact. Enfin, on suppose qu'elle est lisse, c'est à dire, dans le cas où il s'agit d'une variété au sens de la géométrie différentielle, que sur chacun de ses composantes connexes, elle possède en tour point un espace tangent de dimension constante.

Les diviseurs de Weil.

Pour une variété irréductible, propre et lisse, on appelle diviseur sur $X$ une somme formelle, à support fini et à coefficients entiers, de sous-variétés fermées et irréductibles, de codimension 1.

Chaque diviseur de Weil s'écrit donc formellement comme une somme finie

∑	n_iZ_i
i

où les n_i sont des entiers relatifs, tous nuls sauf pour un nombre fini d'entre eux, les Z_i étant des fermés irréductibles de la variété $X$ .

On appelle effectif tout diviseur dont les coefficients sont positifs.

Cas d'une courbe lisse

Sur une courbe lisse, et pour un corps algébriquement clos $K$ , un diviseur de Weil est représenté comme une somme formelle de points de cette courbe, y compris le point à l'infini (on se place sur $P 1, K$ ). La somme formelle 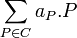$\displaystyle \sum_{P\in C }a_P.P$ étant prise sur une famille à support fini à valeur dans 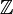$\Z$ , et indexée par les points de $C (K)$

Si le corps n'est pas algébriquement clos, on forme les sommes formelles des places (ou valuations) de la courbe. Un diviseur sur $X$ étant identifié à une combinaison finie,

D =	∑	a_i[x_i]
	i

en prenant un système de représentant des places intervenant dans le diviseur.

quelques propriétés immédiates

Deux diviseurs sont identiques si les coefficients des deux diviseurs pour tout Z_i sont identiques.

La réunion de deux sous-variétés disjointes s'identifiant à leur somme, on munit l'ensemble des diviseurs d'une loi d'additon coefficient par coefficient.

L'ensemble des diviseurs de Weil forment un groupe abélien pour cette addition formelle.

Degré d'un diviseur.

Cas d'un corps quelconque :

Soit $D=\displaystyle \sum_{i\in V }a_i.[x_i]$ un diviseur écrit au travers d'un système complet de représentants des places de la variété $X$ .

Le degré de $D$ est par définition la somme pondérée

deg(D) =	∑	a_i[k(x_i):k],
	i

où $k (x i)$ est le corps résiduel de $X$ en $x i$ .

On montre que l'application qui à tout diviseur associe son degré est un homomorphisme de groupes à valeurs dans ℤ.

Faisceaux définis sur la variété.

Morphismes

On définit dessus ces variétés des morphismes, c'est à dire, localement des applications définies par des fonctions rationnelles partout définies. On obtient ainsi un premier faisceau, celui des morphismes de la variété.

Diviseurs Principaux

Si f est une fonction rationnelle non nulle sur $X$ ; c'est à dire un morphisme de $X$ vers la droite projective, on lui associe un diviseur qui est différence entre le lieu de ses zéros et le lieu de ses pôles (comptés evec leur multiplicité). On note $(f)$ le diviseur de $f$ . Un tel diviseur est dit principal.

On remarque que $(f g) = (f) + (g).$ On en déduit que l'ensemble des diviseurs principaux de la forme $(f)$ pour $f$ rationnelle sur $X$ forme un sous-groupe du groupe des diviseurs de $X$ .

On montre que la somme des multiplicités d'un diviseur principal est nulle. On dit également que ces diviseurs sont linéairement équivalents à 0.

Par définition, deux diviseurs $D$ et $D'$ sont linéairement équivalents si et seulement si leur différence est un diviseur principal.

Le quotient du groupe des diviseurs par le sous-groupe des diviseurs principaux s'appelle groupe de Picard de la variété $X$ .

sections globales

On ordonne les diviseurs par la relation : $D > D'$ si et seulement si $D - D'$ est effectif.

Soit $D$ , un diviseur de $X$ , écrit $D=\sum m_x [x]$ , à la façon de Weil. On considére l'ensemble des fonctions rationnelles $f$ sur $X$ dont le diviseur associé $(f)$ est au moins égal à $- D$

Celles ci, possèdent, sur les sous-variétées $[x]$ où $'' D''$ est positif d'ordre $m [x]$ des pôles de multiplicité au plus $m [x]$ et, sur les sous-variétées [x] où $'' D''$ est négatif, des zéros de multiplicité au moins $- m [x]$ .

Ces fonctions s'appellent les sections globales du faisceau inversible associé au diviseur D.

Faisceaux inversibles

Le faisceau inversible associé à un ouvert de la variété (au sens de Zariski, c'est à dire le complémentaire d'une sous-variété fermée) n'est autre que le faisceau de l'espace vectoriel des sections sur cet ouvert.

Diviseurs de Cartier d'une variété irréductible.

Si la variété $X$ est irréductible mais éventuellement singulière, on définit les diviseurs de Cartier, c'est à dire, localement, le diviseur des zéros d'une fonction rationnelle. plus précisément :

Les diviseurs de Cartier.

Un diviseur de Cartier peut être représenté comme un recouvrement d'ouverts $U i$ , associés à une famille de fonctions rationnelles $f i$ définies sur l'ouvert $U i$ correspondant ; ces fonctions étant reliées entre elles par les changements de cartes admissibles (inversibles et réguliers) entre ces ouverts de façon à ce qu'elles coïncident (à isomorphismes rationnels multiplicatifs près^[1]) sur leur intersection.

En ce sens, un diviseur principal correspond à des fonctions $f i$ régulières. On peut leur associer les sous-variété de codimension 1 qui en sont les zéros et les pôles.

A chaque diviseur de Cartier, on peut donc associer un diviseur de Weil (tous les anneaux locaux sont factoriels); on obtient ainsi un morphisme injectif entre les deux groupes de diviseurs.

Dans le cas d'une variété projective propre et lisse, il s'agit d'un isomorphisme.

Classes d'équivalence, groupe de Picard.

Les classes d'équivalence des diviseurs de Cartier (modulo les diviseurs principaux) correspondent (de façon injective) aux éléments du Groupe de Picard.

Diviseurs de Cartier en termes de faisceaux.

Pour une variété algébrique $X$ , muni des faisceaux $O X$ des fonctions algébriques sur $X$ , et $M X$ des fonctions rationnelles sur X. Un diviseur est une section du groupe quotient $M * / O *$ . L'ensemble de ces sections donnant le groupe des diviseurs de Cartier. On étend ce résultat aux schémas noethériens (dont une variété algébrique est un exemple).

On peut obtient le même résultat en analyse complexe en remplaçant respectivement variété algébrique par variété complexe, algébrique par holomorphes, rationnelles par meromorphes.

A chaque diviseur de Cartier, noté ici $'' D''$ , on peut donc associer une fibre notée O_X(D). La somme des diviseurs correspond alors au produit tensoriel de ces fibres. L'isomorphisme entre fibre correspondant à l'équivalence linéaire des diviseurs de Cartier.

relation entre les diviseurs de Cartier et de Weil.

Si on considère les sections globales du faisceau inversible associé à un diviseur de Cartier, on obtient un injection du groupe des diviseurs de Cartier dans le groupe des diviseurs de Weil.

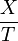
Par exemple : dans la droite projective, ls diviseur défini par soustraction $v O - v I, O$ désignant l'origine et I le point à l'infini, est linéairement équivalent à 0. C'est le diviseur de la fonction $\frac X T$

Les groupes de sections de l'un et de l'autre sont isomorphes : Les fonctions ayant éventuellement un pôle simple en zéro étant isomorphes aux fonctions ayant éventuellement un pôle simple à l'infini.

On montre que cette correspondance entre faisceaux inversibles et diviseurs de Cartier est biunivoque.

Si la variété est singulière ces résultats tombent en défaut.

Un exemple de surface sur laquelle les deux groupes sont différents est donné par la quadrique singulière $X 2 + Y 2 = Z 2$ dans l'espace affine. Une droite passant par le sommet est un diviseur de Weil qui ne correspond à aucun diviseur de Cartier.

Diviseurs remarquables.

Le diviseur canonique

Pour les courbes sur un corps $k$ , algébriquement clos. On considère une fonction non constante, $f$ , définie sur $X$ . la forme différentielle $d f$ sur $X$ s'écrit en tout point $x\in X$ à l'aide d'une coordonnée $t$ de $X$ (un paramètre admissible). Il existe une fonction rationnelle $g$ telle que $d f = g (x) d t$

On appelle l'ordre de $d f$ , et on le note $v x (d f)$ l'ordre de $g$ en $x$ .

On considére alors le diviseur $(df):=\sum_{x\in X}v_x(df)[x]$ . Ce diviseur sur $X$ , est un représentant du diviseur canonique de $X$ .

Cette nomination étant justifié par le fait que pour une autre fonction rationnelle, le diviseur canonique associés est linéairement équivalent au premier. Ainsi, le diviseur canonique apparaît pour sa part comme un élément du groupe de Picard.

Diviseur à l'infini , faisceaux amples

Un diviseur de l'espace projectif, est défini par l'hyperplan à l'infini (avec multiplicité 1).

À équivalence linéaire près, il est équivalent au diviseur défini par n'importe quel hyperplan.

On note $O (1)$ le faisceau de ses sections (ou faisceau inversible associé). Ce faisceau est appelé le faisceau de Serre : une section de $O (1)$ est une fonction rationnelle qui a au plus un pôle simple (à l'infini ou ailleurs)

Un faisceau inversible est dit très ample lorsqu'on peut plonger la variété comme une variété fermée dans un espace projectif de façon que le diviseur (associé au faisceau) soit l'intersection de la variété avec le diviseur défini ci-dessus

Un faisceau ample est un faisceau dont une certaine puissance tensorielle (positive) est très ample.

Une condition (CNS) pour qu'un faisceau soit ample est que le degré du diviseur associé soit strictement positif.

Le langage des Anneaux.

Weil en termes d'anneaux.

Si A désigne un anneau. On appelle diviseur de Weil une combinaison lineaire `a coefficients entiers de quotients $A / p$ de l'anneau A par des ideaux premiers $P$ tels que $d i m (A P) = 1$ .

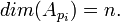
Si $n$ est un entier, un cycles de codimension $n$ , noté $Z n (A)$ est une combinaison lineaire de type $\sum_{i=1}^n n_i.[A/p_i]$ où les $n i$ sont entiers et les $P i$ des ideaux premiers de A tels que $dim(A_{p_i})= n.$

Ainsi les diviseurs de Weil sont les cycles de codimension un.

Exemple :

Si I est un ideal de $A$ et $A$ un anneau noetherien ; si $d i m (A / p) / g e q n$ pour tout ideal premier de I, on peut lui associer un cycle de codimension n ; noté $c y c l e (A / I) A$ et défini par :

$cycle(A/I) A=\sum_{ dim A_p=n }long((A/p)/(IA/p))[A/p]$

La somme étant finie.

Lorsque I est un A-module inversible (c'est-à-dire, si I est localement engendré par un élément non diviseur de zero) on obtient un diviseur de Weil^[2]. On note $Z 1 (A)$ leur ensemble.

Cartier en termes d'anneaux.

Soit $A$ un anneau. On appelle groupe des diviseurs de Cartier de $A$ , et on note $D i v (A)$ le groupe engendre par le monoïde des ideaux(A-modules) inversibles.

On voit que si I et J sont deux ideaux dans $D i v (A)$ alors 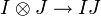$I \otimes J \to IJ$ est un isomorphisme. On montre pour finir le lemme suivant :

Si A est un anneau de Dedekind l’application cycle : 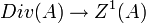$Div(A)\to Z^1(A)$ est surjective.

Diviseurs principaux, Groupe de Picard.

Définition

Toujours sur un anneau, noté $A$ . On appelle diviseurs principaux de $A$ , et on note $P r (A)$ le sous-groupe de $D i v (A)$ engendre par les ideaux $f A$ où $f$ est non-diviseur de zero. Ce groupe est canoniquement isomorphe `a $K * / A$

Si $A$ , est un anneau de Dedekind, $K$ , son corps de fractions et $f$ , un élément de $K$ , alors $(f) =\sum dim A/p= vp(f)[A/p]$ est un élément de $Z 1 (A)$ dans l’image de $P r (A)$ . (vp étant la valuation associee `a $A P$ ).

Proposition

Avec les notations introduites ci-dessus si A est intègre on a la suite exacte :

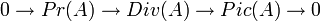
$0 \to Pr(A) \to Div(A) \to Pic(A) \to 0$

Sources Web

↑ [1]
↑ [2]

Bibliographie

Joseph L. Taylor: Several Complex Variables with Connections to Algebraic Geometry and Lie Groups. American Mathematical Society 2002, ISBN 0-8218-3178-X
William Fulton: Algebraic Curves. An Introduction to Algebraic Geometry. Mathematics note lecture series, 30 Benjamin / Cummings, New York 1969, ISBN 0-201-51010-3
Robin Hartshorne: Algebraic Geometry. Springer-Verlag 1977. ISBN 0-387-90244-9

Reinhold Remmert, Georg Schumacher: 2e fonction théorie Springer, Berlin, 2007, ISBN 978-3-540-57052-3

Catégories: Théorie de la fonction | géométrie algébrique

Jean Dieudonné History of algebraic geometry. An outline of the history and development of algebraic geometry | isbn=0-534-03723-2
Hartshorne Robin Algebraic Geometry | isbn=0-387-90244-9

Portail des mathématiques

Ce document provient de « Diviseur (g%C3%A9om%C3%A9trie alg%C3%A9brique) ».

Catégorie : Géométrie algébrique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Groupe de diviseurs de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Groupe des diviseurs — Diviseur (géométrie algébrique) Les Diviseurs de Weil et de Cartier sont des outils de la géométrie algébrique. En géométrie algébrique, comme en analyse complexe, ou en géométrie arithmétique, les diviseurs forment un groupe qui permet de saisir … Wikipédia en Français
Groupe de Picard — En géométrie algébrique, le groupe de Picard est un groupe associé à une variété algébrique ou plus généralement à un schéma. Il est en général isomorphe au groupe des diviseurs de Cartier. Si K est un corps de nombres, le groupe de Picard de l… … Wikipédia en Français
Groupe Diédral — Symétrie bidimensionnelle D4 En mathématiques, le groupe diédral noté Dn, pour , ou parfois D2n, est un groupe d ordre 2n qui s interprète notamment comme le groupe des … Wikipédia en Français
Groupe diedral — Groupe diédral Symétrie bidimensionnelle D4 En mathématiques, le groupe diédral noté Dn, pour , ou parfois D2n, est un groupe d ordre 2n qui s interprète notamment comme le groupe des … Wikipédia en Français
Groupe dihédral — Groupe diédral Symétrie bidimensionnelle D4 En mathématiques, le groupe diédral noté Dn, pour , ou parfois D2n, est un groupe d ordre 2n qui s interprète notamment comme le groupe des … Wikipédia en Français
Groupe Alterné — En mathématiques, et plus précisément en théorie des groupes, le groupe alterné de degré n, souvent noté An, est un sous groupe distingué du groupe symétrique des permutations d un ensemble fini de cardinal n. Ce sous groupe est composé des… … Wikipédia en Français
Groupe alterne — Groupe alterné En mathématiques, et plus précisément en théorie des groupes, le groupe alterné de degré n, souvent noté An, est un sous groupe distingué du groupe symétrique des permutations d un ensemble fini de cardinal n. Ce sous groupe est… … Wikipédia en Français
Groupe diédral — Symétrie bidimensionnelle D4 En mathématiques, le groupe diédral noté Dn, pour , ou parfois D2n, est un groupe d ordre 2n qui s interprète notamment comme le groupe des isométries du plan conservant un … Wikipédia en Français
Groupe abélien de type fini — En mathématiques, un groupe abélien de type fini est un groupe abélien qui possède une partie génératrice finie. Les produits, les quotients, mais aussi les sous groupes des groupes abéliens de type fini sont eux mêmes de type fini. Un théorème… … Wikipédia en Français
Groupe alterné — En mathématiques, et plus précisément en théorie des groupes, le groupe alterné de degré n, souvent noté An, est un sous groupe distingué du groupe symétrique des permutations d un ensemble fini à n éléments. Ce sous groupe est composé des… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Groupe de diviseurs

Diviseur (géométrie algébrique)

Sommaire