- Intervalle ouvert
-
Intervalle (mathématiques)
En mathématiques, un intervalle (du latin intervallum) est étymologiquement un ensemble compris entre deux valeurs. Cette notion première s'est ensuite développée jusqu'à aboutir aux définitions suivantes.
Sommaire
Intervalles de R
Inventaire
Initialement, on appelle intervalle réel un ensemble de nombres délimité par deux nombres réels constituant une borne inférieure et une borne supérieure. Un intervalle contient tous les nombres réels compris entre ces deux bornes.
Cette définition regroupe les intervalles des types suivants (avec
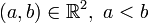 ):
):Les intervalles du premier type sont appelés intervalles ouverts; les seconds intervalles fermés, et les deux derniers intervalles semi-ouverts.
La notation anglaise "set builder" [1] (doc de matlab ou octave par ex.) utilise la parenthèse dans le 'bon' sens pour les limites ouvertes: (0,1) est alors l'intervalle de 0 à 1, bornes exclues, et rand dans ces outils retourne un résultat dans cet intervalle.
À ces intervalles se sont ajoutés les ensembles des réels inférieurs à une valeur, ou supérieurs à une valeur. On ajoute donc les intervalles de ce type :
Auxquels se sont ajoutés, pour faire bonne mesure, les intervalles :
Définition générale
Un intervalle de
 est une partie
est une partie 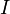 de
de  vérifiant la propriété suivante:
vérifiant la propriété suivante:Un ensemble vérifiant une telle propriété est un ensemble convexe.
Les intervalles de
 regroupent donc toutes les parties convexes de
regroupent donc toutes les parties convexes de  .
.Union et intersection d'intervalles de

Une intersection d'intervalles de
 est toujours un intervalle. L'intervalle qui découle d'une intersection d'intervalles est composé des éléments (les nombres) qui sont présents à la fois dans le premier intervalle et dans le second intervalle. Par exemple,
est toujours un intervalle. L'intervalle qui découle d'une intersection d'intervalles est composé des éléments (les nombres) qui sont présents à la fois dans le premier intervalle et dans le second intervalle. Par exemple,Une union d'intervalles de
 n'est pas toujours un intervalle. Ce sera un intervalle si l'ensemble obtenu reste convexe (intuitivement s'il n'y a pas de "trou"). Dans le cas d'une union de deux intervalles, il suffit que l'intersection de ces intervalles soit non vide pour que leur réunion soit convexe. Par exemple,
n'est pas toujours un intervalle. Ce sera un intervalle si l'ensemble obtenu reste convexe (intuitivement s'il n'y a pas de "trou"). Dans le cas d'une union de deux intervalles, il suffit que l'intersection de ces intervalles soit non vide pour que leur réunion soit convexe. Par exemple,![]- \infty; 2] \cup [-3; 5[= ]- \infty; 5[](/pictures/frwiki/48/0cc3affccbcff9d7f0d6703fd4ba891c.png)
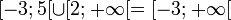
![[3; 5[ \cup ]- \infty; 2] = ]- \infty; 2] \cup [3; 5[](/pictures/frwiki/55/7b90ee82d0c295b6b6893e8891bbb35c.png) (On préfère ranger les intervalles par ordre croissant de leurs bornes.)
(On préfère ranger les intervalles par ordre croissant de leurs bornes.)
Cette union ne forme pas un intervalle étant donné qu'il y a un trou entre 2 et 3.
Connexité et compacité
Les parties connexes de
 (pour la topologie usuelle) sont exactement les intervalles.
(pour la topologie usuelle) sont exactement les intervalles.Les intervalles fermés c'est-à-dire contenant leurs bornes sont appelés segments. Ce sont les seuls intervalles compacts. Ce résultat est un cas particulier du théorème de Borel-Lebesgue.
Décomposition des ouverts de R
On montre que tout ouvert de
 peut s'écrire comme une réunion dénombrable d'intervalles ouverts.
peut s'écrire comme une réunion dénombrable d'intervalles ouverts.En analyse et en topologie
Les intervalles sont les parties de
 les plus intéressantes dès que l'on parle de continuité et de dérivabilité.
les plus intéressantes dès que l'on parle de continuité et de dérivabilité.On trouve alors (entre autres) pour les fonctions réelles d'une variable réelle, des propriétés telles que :
- L'image par une fonction continue d'un intervalle de
 est un intervalle de
est un intervalle de  (théorème des valeurs intermédiaires)
(théorème des valeurs intermédiaires) - Une fonction dérivable et à dérivée identiquement nulle sur un intervalle est constante sur cet intervalle.
- Une fonction dérivable est monotone sur un intervalle si et seulement si sa dérivée garde un signe constant sur cet intervalle
Remarque : La fonction
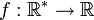 définie par
définie par 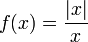 est dérivable sur
est dérivable sur 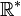 , et sa dérivée est identiquement nulle ; mais
, et sa dérivée est identiquement nulle ; mais 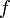 n'est pas constante. Ceci tient au fait que
n'est pas constante. Ceci tient au fait que 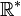 n'est pas un intervalle.
n'est pas un intervalle.Intervalle dans un ensemble muni d'une relation d'ordre total
Dans tout ensemble
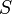 muni d'une relation d'ordre total
muni d'une relation d'ordre total 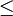 , on peut définir des intervalles, de la même façon que dans
, on peut définir des intervalles, de la même façon que dans  , comme des ensembles des types suivants :
, comme des ensembles des types suivants :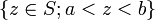 ,
, 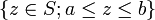 ,
, 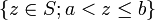 ,
, 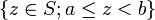
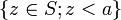 ,
, 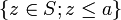 ,
, 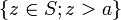 ,
, 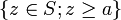
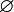 ,
, 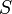
Les quatre premières notations généralisent respectivement l'intervalle ouvert, l'intervalle fermé, l'intervalle semi-ouvert à gauche et l'intervalle semi-ouvert à droite. La cinquième notation est un cas particulier de section commençante ouverte ;[1] les trois suivantes sont la section commençante fermée, la section finissante ouverte[2] et la section finissante fermée déterminées par a, respectivement.
Il est donc tout à fait possible de définir dans
 l'intervalle des entiers relatifs compris entre
l'intervalle des entiers relatifs compris entre 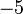 et
et 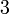 mais il serait dangereux de le noter
mais il serait dangereux de le noter ![\ [-5;3]](/pictures/frwiki/52/4d25b770fbfdb26c8d019ca5ef3bc7e7.png) sans avertissement préalable à cause du risque de confusion avec la notation des intervalles de
sans avertissement préalable à cause du risque de confusion avec la notation des intervalles de  . On utilise parfois la notation avec des crochets blancs 〚 − 5;3〛.
. On utilise parfois la notation avec des crochets blancs 〚 − 5;3〛.Ces intervalles
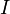 vérifient toujours la propriété :
vérifient toujours la propriété :Pour tous éléments
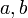 de
de 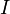 , on a
, on a ![[a; b] \subset I](/pictures/frwiki/101/ee72a6304b54895704b227b11c210abe.png) (convexité d'un intervalle) ,
(convexité d'un intervalle) ,ainsi que la propriété d'intersection : toute intersection d'intervalles est un intervalle.
Notes et références
- ↑ Ce n'est qu'un cas particulier, car il peut exister des sections commençantes ouvertes dont a n'est pas la borne supérieure - c'est notamment le cas des coupures de Dedekind qui définissent un nombre réel et n'ont pas nécessairement de borne supérieure dans Q
- ↑ Remarque analogue : une section finissante n'a pas nécessairement une borne inférieure
Articles connexes
- Portail des mathématiques
Catégories : Espace topologique remarquable | Théorie des ordres | Analyse
Wikimedia Foundation. 2010.

![\{x \in \mathbb{R} ; a < x < b \} = ]a; b[](/pictures/frwiki/48/0a43ac756b63695c3b298fd69d328c9c.png)
![\{x \in \mathbb{R} ; a \leq x \leq b \} = [a ; b]](/pictures/frwiki/100/d20db45d2d302e0aa8ddb4b9efa7b127.png)
![\{x \in \mathbb{R} ; a < x \leq b \} = ]a; b]](/pictures/frwiki/48/0c02828f2141a76d538b68275879c52a.png)
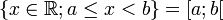
![\left\{x \in \mathbb{R} ; x < a\right\} = ]-\infty; a[](/pictures/frwiki/55/72a538ea7c47b647f9387787fd4cd4d1.png)
![\left\{x \in \mathbb{R} ; x \leq a\right\} = ]-\infty; a]](/pictures/frwiki/54/67770b07245dfa1c1b08913b07293bea.png)
![\left\{x \in \mathbb{R} ; x > a \right\} = ]a; +\infty[](/pictures/frwiki/99/c7bfa6a84c73b318898a0a608dee99b3.png)
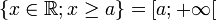
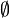
![\left\{a\right\} = [a; a]](/pictures/frwiki/98/b67f826b2962ce098c323e97ab5c90db.png)
![\mathbb{R} = ]-\infty; +\infty[](/pictures/frwiki/99/c831c4db34fa36a0c0398ff41c1bdc55.png)
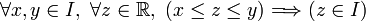
![[-3; 5[ \cap ]- \infty; 2] = [-3; 2]](/pictures/frwiki/97/aa09968de2f938f00a23755ffcad7487.png)
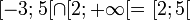
![[3; 5[ \cap ]- \infty; 2] = \emptyset](/pictures/frwiki/56/8913200d15d27982208c41ec094ff4f6.png)