Pôle et polaire

En géométrie, la relation pôle/polaire est une relation qui, un cercle étant donné, associe entre eux les points et les droites du plan.

Dans cette association, on dit de la droite qu'elle est la polaire du point, et du point qu'il est le pôle de la droite (sous-entendu : par rapport au cercle donné).

Fig.1. La polaire du point P par rapport au cercle (C) passe par les points de tangence des droites tangentes à (C) menées par P.

Fig. 2. La polaire du point P est la droite (d). On note qu'elle est perpendiculaire à la droite PO (O centre du cercle (C).

Fig. 3. Pôle P de la droite (d) par rapport à la conique (C). La construction, qui résulte également des propriétés du quadrilatère complet, est calquée sur la précédente.

Définition harmonique

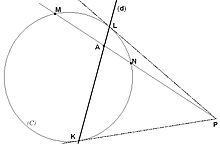
• Soient (C) un cercle, et P un point du plan.
• Considérons un point M mobile sur (C).
• Soit N le deuxième point d'intersection de (MP) et (C).
• Soit enfin A le point tel que P,A,M,N forment une division harmonique, c'est-à-dire tel que le birapport (PA,MN) vaut -1. On montre que, lorsque M varie, le lieu de A est un segment de droite.

Si P est extérieur à (C), on peut mener par ce point deux tangentes au cercle . Appelons K et L les points de contact au cercle de ces tangentes. Alors, la polaire (d) du point P est la droite (KL) (voir figure).

Propriétés

• La polaire d'un point P par rapport à un cercle de centre O est une droite perpendiculaire à OP.
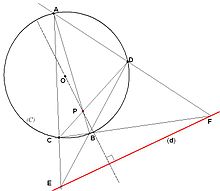
• Soient A,B,C,D quatre points d'un cercle (C). Soit par ailleurs:
  • ,
  • ,
  • .

Alors, d'après les propriétés du quadrilatère complet la polaire de P par rapport à (C) est la droite (FE) (voir figure 1).

Cette propriété permet de construire la polaire d'un point à la règle uniquement, et aussi de la tracer pour un point intérieur au cercle.

On pourra également, en s'aidant de cette propriété construire, à la règle seulement, les tangentes à un cercle passant par un point extérieur au cercle.

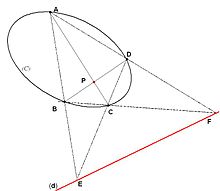
Généralisation aux coniques

Du fait que les transformations homographiques du plan (c'est-à-dire les perspectives de perspectives coniques) conservent le birapport, on peut généraliser les propriétés précédentes.

La transformée d'un point par homographie est un point. Celle d'une droite est une droite. Celle d'un cercle est une conique dont la nature dépend de l'homographie. Les homographies conservent les alignements de points et les intersections.

On pourra donc appeler polaire d'un pôle par rapport à une conique, l'ensemble des points qui définit des divisions harmoniques avec les intersections avec la conique des droites passant par le pôle.

Articles connexes

François-Joseph Servois (le premier à employer le mot « pôle » en géométrie projective)

• Portail de la géométrie