- Hexagone magique
-
En mathématiques, un hexagone magique d'ordre n est un arrangement de nombres formant un gabarit hexagonal centré avec n cellules sur chaque côté. La somme des nombres dans chaque rangée ou dans les trois directions font la même somme. Un hexagone magique normal contient tous les entiers allant de 1 à 3n2 − 3n + 1. Il existe seulement deux arrangements respectant ces conditions, celui d'ordre 1 et celui d'ordre 3. De plus, la solution d'ordre 3 est unique[1]. Meng en donne une preuve constructive [2].
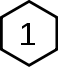

Ordre 1 Ordre 3 M = 1 M = 38 L'hexagone d'ordre 3 a été publié à plusieurs reprises comme une « nouvelle » découverte. La plus vieille référence sur le sujet remonte à Ernst von Haselberg en 1887.
Il existe des hexagones non normaux d'ordre supérieur à 3. La suite numérique commence avec une nombre différent de 1. Arsen Zahray a découvert ces hexagones d'ordre 4 et 5 :
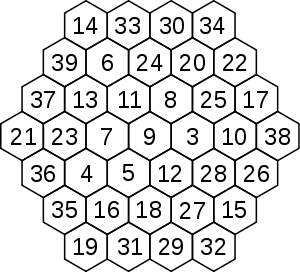
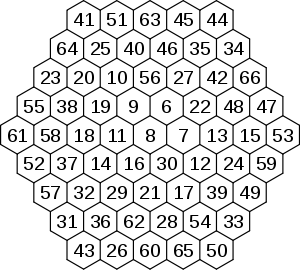
Ordre 4 (non normal) Ordre 5 (non normal) (commence à 3 et se termine à 39) (commence à 6 et se termine à 66) M = 111 M = 244 Un hexagone d'ordre 6 a été publié par Louis Hoelbling le 11 octobre 2004 :

Ordre 6 (non normal) (commence à 21 et se termine à 111) M = 546 Un hexagone d'ordre 7 a été publié par Arsen Zahray le 22 mars 2006 (il a fait appel au recuit simulé) :
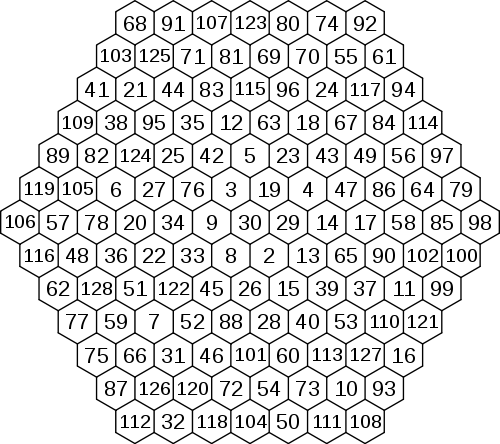
Ordre 7 (non normal) (commence à 2 et se termine à 128) M = 635 Un hexagone d'ordre 8 a été publié par Louis K. Hoelbling le 5 février 2006 :

Ordre 8 (non normal) (commence à -84 et se termine à 84) M = 0 Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Magic hexagon » (voir la liste des auteurs)
Bibliographie
- (en) J. E. Baker et D. R. King, « The use of visual schema to find properties of a hexagon », Visual Mathematics, Vol. 5, Number 3, 2004.
- (en) J. E. Baker et A. J. Baker, « The hexagon, nature's choice », Archimedes, Vol. 4, 2004.
Notes
- (en) C. W. Trigg, « A Unique Magic Hexagon », Recreational Mathematics Magazine, January-February 1964. Consulté le 2009-12-16.
- (en) [PDF] Meng, F. « Research into the Order 3 Magic Hexagon », Shing-Tung Yau Awards, October 2008. Consulté le 2009-12-16.
Wikimedia Foundation. 2010.
