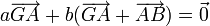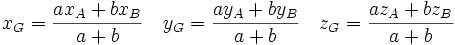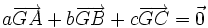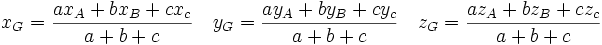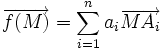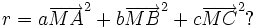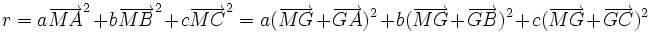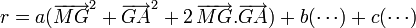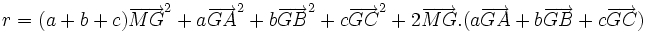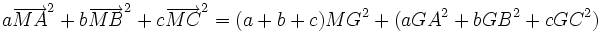Barycentre (géométrie euclidienne)

Pour les articles homonymes, voir Barycentre.

En géométrie, le barycentre est un point qui permet de résumer un ensemble géométrique sur lequel sont réparties des valeurs numériques. Ces valeurs peuvent représenter des poids pour déterminer le point d'équilibre d'un mobile. Mais le barycentre permet aussi de caractériser le centre d'inertie d'un solide ou concentrer un ensemble de charges électriques.

Mathématiquement, le barycentre s'obtient en annulant une relation vectorielle. Cette notion généralise la construction du milieu d'un segment ou du centre de gravité d'un triangle.

Sommaire

1 Barycentre de deux points
2 Barycentre de trois points dans le plan ou dans l'espace
3 Barycentre de n points
- 3.1 Réduction de fonctions vectorielles ou du second degré
- 3.2 Exemple pratique
4 Voir aussi

Barycentre de deux points

Point d'équilibre

Le terme de barycentre est formé sur la racine grecque barus (lourd) pour désigner un centre des poids ou centre d'équilibre. Sa conception est liée au théorème des moments découvert par Archimède au III^e siècle av. J.-C.

Point d'équilibre d'une balance

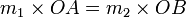Pour que la balance soit en équilibre, il faut que les moments, c'est-à-dire les produits des longueurs de bras par les masses correspondantes, soient égaux. Autrement dit le point d'équilibre est caractérisé par la relation : $m_1\times OA = m_2 \times OB$ .

Par exemple, si la masse $m 1$ est 4 fois plus importante que la masse $m 2$ , il faudra que la longueur $O A$ soit 4 fois plus petite que la longueur $O B$ .

Ce principe des moments est d'ailleurs utilisé dans la balance dite romaine

Les poids peuvent également avoir une valeur numérique négative, si l'une des masses est remplacée par un ballon d'hélium, par exemple. Dans ce cas, le point d'équilibre se situe en dehors de l'espace délimité par les deux objets.

Relation vectorielle

En géométrie affine, le point d'équilibre, ou barycentre, est noté $G$ et les poids des points fixes $A$ et $B$ sont notés usuellement $a$ et $b$ . Le théorème des moments est remplacé par la relation

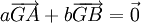$a\overrightarrow{GA}+ b\overrightarrow{GB}=\vec 0$ .

À l'aide de la relation de Chasles, cette relation peut se réécrire sous la forme

$a\overrightarrow{GA} + b(\overrightarrow{GA}+\overrightarrow{AB})=\vec 0$

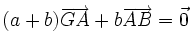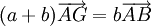c'est-à-dire $(a+b)\overrightarrow{GA} + b\overrightarrow{AB}=\vec 0$ ou de manière équivalente $(a+b)\overrightarrow{AG} = b\overrightarrow{AB}$ .

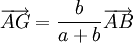Si la somme $a + b$ est non nulle, il existe un unique point $G$ qui satisfait cette relation, donné par la relation $\overrightarrow{AG} = \frac{b}{a+b} \overrightarrow{AB}$ .

Colinéarité

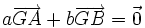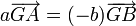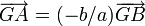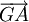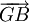De la définition $a\overrightarrow{GA} + b\overrightarrow{GB} = \vec 0$ , on tire que $a\overrightarrow{GA} = (-b)\overrightarrow{GB}$ ou encore que $\overrightarrow{GA} = (-b/a)\overrightarrow{GB}$ ; ainsi $\overrightarrow{GA}$ et $\overrightarrow{GB}$ sont colinéaires et ont un point en commun, G. Par conséquent, G appartient à la droite (AB). Nous venons de démontrer que

si G est le barycentre de {(A,a),(B,b)} alors G appartient à la droite (AB).

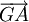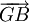Si G est sur le segment [AB] (entre A et B) alors $\overrightarrow{GA}$ et $\overrightarrow{GB}$ sont de sens opposé, ce qui se traduit par 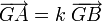$\overrightarrow{GA} = k\; \overrightarrow{GB}$ avec k< 0. Mais, comme dans le même temps 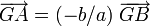$\overrightarrow{GA} = (-b/a)\; \overrightarrow{GB}$ , on en déduit que b et a sont de même signe. Nous venons de démontrer que

Si G est sur le segment [AB] (entre A et B) alors a et b sont de même signe.

Coordonnées barycentriques

On démontre (à démontrer ultérieurement) que, si A et B sont distincts, tout point M de la droite (AB) peut s'écrire comme barycentre des points A et B. Les pondérations obtenues sont appelées les coordonnées barycentriques du point M.

Homogénéité

Si G est le barycentre de ${(A, a);(B, b)}$ alors, 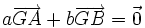$a\overrightarrow{GA} + b\overrightarrow{GB} = \vec 0$ , et il vient que pour tout réel k 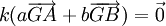$k(a\overrightarrow{GA} + b\overrightarrow{GB}) = \vec 0$ . Autrement dit, on obtient 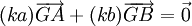$(ka)\overrightarrow{GA} + (kb)\overrightarrow{GB} = \vec 0$ De plus, comme $a + b$ est non nul, pour tout $k$ réel non nul, $k (a + b)$ est également non nul. Alors G est le barycentre de ${(A, k . a);(B, k . b)}$ .

Nous venons de démontrer que

si G est le barycentre de ${(A, a);(B, b)}$ alors pour tout k réel non nul, G est aussi le barycentre de ${(A, k a);(B, k b)}$ .

Cette propriété s'appelle l'homogénéité.

Réduction

L'application de la relation de Chasles à 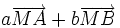$a\overrightarrow{MA} + b\overrightarrow{MB}$ , en introduisant le barycentre G de $(A, a),(B, b)$ donne

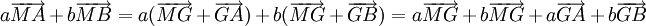$a\overrightarrow{MA} + b\overrightarrow{MB} = a(\overrightarrow{MG}+\overrightarrow{GA}) + b(\overrightarrow{MG}+\overrightarrow{GB}) = a\overrightarrow{MG} + b\overrightarrow{MG} + a\overrightarrow{GA}+ b\overrightarrow{GB}$ .

G étant barycentre de $(A, a),(B, b)$ alors 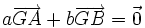$a\overrightarrow{GA} + b\overrightarrow{GB} = \vec 0$ . La relation précédente devient:

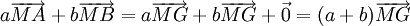$a\overrightarrow{MA} + b\overrightarrow{MB} =a\overrightarrow{MG} + b\overrightarrow{MG}+ \vec 0 = ( a+b)\overrightarrow{MG}$ .

Nous venons de démontrer que

si G est le barycentre de $(A, a),(B, b)$ alors pour tout M du plan,

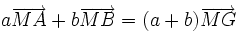$a\overrightarrow{MA} + b\overrightarrow{MB} = (a+b)\overrightarrow{MG}$ .

C'est la propriété de réduction.

Elle permet de positionner le point G par rapport à tout point M. Si M est l'origine d'un repère du plan ou de l'espace, elle permet de définir les coordonnées du point G

$x_G = \frac{ax_A+bx_B}{a+b} \quad y_G = \frac{ay_A+by_B}{a+b}\quad z_G = \frac{az_A+bz_B}{a+b}$

Barycentre de trois points dans le plan ou dans l'espace

La définition peut se généraliser à trois points : pour tous réels a, b et c tels que a + b + c soit non nul, il existe un unique point G tel que

$a\overrightarrow{GA} + b\overrightarrow{GB} + c\overrightarrow{GC}= \vec 0$

appelé barycentre du système pondéré ${(A, a);(B, b);(C, c)}$ . Les points G, A, B et C sont toujours coplanaires et on démontre que , si A, B, C définissent un plan, tous les points M de ce plan peuvent s'écrire comme barycentre de A, B et C. Les pondérations s'appellent alors coordonnées barycentriques de M dans le repère A, B et C

Comme pour le barycentre de deux points, le barycentre de trois points permet de réduire l'expression vectorielle 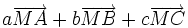$a\overrightarrow{MA} + b\overrightarrow{MB} + c\overrightarrow{MC}$ , pour tout point M :

$a\overrightarrow{MA} + b\overrightarrow{MB} + c\overrightarrow{MC} = (a+b+c)\overrightarrow{MG}$

Ce qui permet, en remplaçant M par l'origine du repère, de donner les coordonnées du point G

$x_G = \frac{ax_A+bx_B + cx_c}{a+b+c} \quad y_G = \frac{ay_A+by_B+cy_c}{a+b+c} \quad z_G = \frac{az_A+bz_B+cz_c}{a+b+c}$

Ce barycentre possède en outre une propriété dite d'associativité ou de barycentre partiel : si a + b est non nul et si $G 1$ est le barycentre du système ${(A, a);(B, b)}$ , alors G est le barycentre du système ${(G 1, a + b);(C, c)}$ . Cela signifie que la construction du barycentre de trois points peut se ramener à la construction de barycentres de deux points.

Cette propriété simplifie grandement les problèmes d'alignement et de concours.

En considérant ces trois points comme les sommets d’un triangle, le centre de gravité est le point d'intersection de ses 3 médianes. Le centre de gravité est situé aux $\frac{2}{3}$ d'une médiane en partant du sommet.
Autrement dit, soit un triangle ABC, A' le milieu de [BC], B' le milieu de [AC], et C' le milieu de [AB] et G son centre de gravité.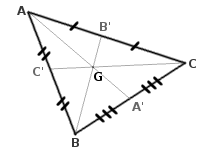

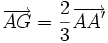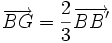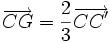Alors : $\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AA'}$ , $\overrightarrow{BG}=\frac{2}{3}\overrightarrow{BB'}$ et $\overrightarrow{CG}=\frac{2}{3}\overrightarrow{CC'}$ .

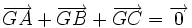Le centre de gravité est aussi l' isobarycentre des sommets du triangle, c'est-à-dire que $\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0}$ .

Barycentre de n points

On peut généraliser la définition à n points dans un espace affine E quelconque. On définit alors une fonction f de E dans 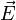$\vec E$ , appelée fonction vectorielle de Leibniz :

$\overrightarrow{f(M)} = \sum_{i = 1}^n a_i\overrightarrow{MA_i}$

On démontre que si 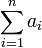$\sum_{i = 1}^n a_i$ est non nul, la fonction s'annule pour un unique point G appelé barycentre du système ${(A i, a i)} i = 1... n$ . Ce point G est toujours dans le sous-espace affine engendré par les $(A i)$ . Réciproquement, si les $A i$ constituent une famille libre de n points d'un sous-espace affine F de dimension n - 1, tout point M de F peut s'écrire comme barycentre des points ( $A i$ ). Les pondérations s'appellent les coordonnées barycentriques de G dans le repère ( $A i$ ).

Réduction de fonctions vectorielles ou du second degré

Article détaillé : Fonctions de Leibniz.

À partir du barycentre, il est possible de réduire des expressions vectorielles. Prenons l'exemple de 3 points seulement A B C de poids a b c et leur barycentre G. La formule du premier degré est celle du barycentre :

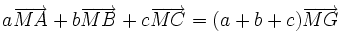$a\overrightarrow{MA} + b\overrightarrow{MB} + c\overrightarrow{MC} = (a+b+c)\overrightarrow{MG}$ qui permet de nombreux calculs du premier degré sur les vecteurs.

A partir du barycentre il est possible de définir une formule du second degré, au sens du produit scalaire des vecteurs : Que peut-on dire de la formule du second degré suivante, dont le résultat est un nombre r

$r= a\overrightarrow{MA}^2 + b\overrightarrow{MB}^2 + c\overrightarrow{MC}^2 ?$

Remplaçons chaque vecteur 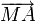$\overrightarrow{MA}$ etc par 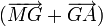$(\overrightarrow{MG}+\overrightarrow{GA})$ et appliquons la formule du carré d'une somme:

$r= a\overrightarrow{MA}^2 + b\overrightarrow{MB}^2 + c\overrightarrow{MC}^2 = a( \overrightarrow{MG}+ \overrightarrow{GA} )^2 + b(\overrightarrow{MG}+ \overrightarrow{GB})^2 + c(\overrightarrow{MG}+ \overrightarrow{GC})^2$

$r= a( \overrightarrow{MG}^2+ \overrightarrow{GA}^2 + 2\,\overrightarrow{MG}.\overrightarrow{GA})+ b(\cdots)+c(\cdots)$

$r= (a+b+c)\overrightarrow{MG}^2+a\overrightarrow{GA}^2 + b\overrightarrow{GB}^2 + c\overrightarrow{GC}^2 + 2\overrightarrow{MG}.(a\overrightarrow{GA} + b\overrightarrow{GB} + c\overrightarrow{GC})$

Les doubles produits s'annulent, d'où le résultat

$a\overrightarrow{MA}^2 + b\overrightarrow{MB}^2 + c\overrightarrow{MC}^2 = (a+b+c){MG}^2+(a{GA}^2 + b{GB}^2 + c{GC}^2)$

au second degré où seul le terme $M G 2$ est variable.

Rappelons la formule de départ du premier degré

$a\overrightarrow{MA} + b\overrightarrow{MB} + c\overrightarrow{MC} = (a+b+c)\overrightarrow{MG}$

Exemple pratique

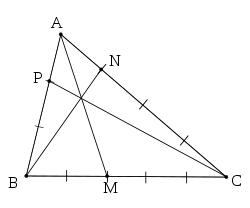
Article détaillé : Théorème de Ceva.

Figure 2

Dans le dessin ci-contre (figure 2), les graduations sur chaque côté sont régulières. Les droites (AM) (BN) et (CP) sont concourantes.

Démonstration

La lecture du dessin permet de dire que

P est barycentre du système {(A ; 2), (B ; 1)}
N est barycentre du système {(A ; 3), (C ; 1)}
M est barycentre du système {(B ; 3), (C ; 2)}

La propriété d'homogénéité du barycentre permet de dire que

P est barycentre du système {(A ; 6), (B ; 3)}
N est barycentre du système {(A ; 6), (C ; 2)}
M est barycentre du système {(B ; 3), (C ; 2)}

Il suffit alors de créer un point G barycentre du système {(A ; 6) , (B ; 3) ; (C ; 2)} et d'utiliser trois fois la propriété d'associativité

G est barycentre du système {(P ; 9), (C ; 2)} donc G est sur la droite (PC)
G est barycentre du système {(N ; 8), (B ; 3)} donc G est sur la droite (NB)
G est barycentre du système {(M ; 5), (A ; 6)} donc G est sur la droite (AM)

G est donc le point de concours des trois droites.

Voir aussi

Portail de la géométrie

Ce document provient de « Barycentre (g%C3%A9om%C3%A9trie euclidienne) ».

Catégorie : Géométrie euclidienne

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Barycentre (géométrie euclidienne) de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Barycentre (Géométrie Euclidienne) — Pour les articles homonymes, voir Barycentre. En géométrie, le barycentre est un point qui permet de résumer un ensemble géométrique sur lequel sont réparties des valeurs numériques. Ces valeurs peuvent représenter des poids pour déterminer le… … Wikipédia en Français
Barycentre (Géométrie Affine) — Pour les articles homonymes, voir Barycentre. En géométrie affine, le barycentre de plusieurs points affectés de coefficients est un point annulant une certaine égalité vectorielle. Le calcul de barycentre est l outil fondamental de la géométrie… … Wikipédia en Français
Barycentre (mathématiques) — Barycentre (géométrie euclidienne) Pour les articles homonymes, voir Barycentre. En géométrie, le barycentre est un point qui permet de résumer un ensemble géométrique sur lequel sont réparties des valeurs numériques. Ces valeurs peuvent… … Wikipédia en Français
Barycentre (mathématiques élémentaires) — Barycentre (géométrie euclidienne) Pour les articles homonymes, voir Barycentre. En géométrie, le barycentre est un point qui permet de résumer un ensemble géométrique sur lequel sont réparties des valeurs numériques. Ces valeurs peuvent… … Wikipédia en Français
Geometrie affine — Géométrie affine La géométrie affine est la géométrie des espaces affines : il s agit grossièrement d ensembles de points définis par des propriétés spécifiques permettant de parler d alignement, de parallélisme, d intersection. Les notions… … Wikipédia en Français
Géométrie Affine — La géométrie affine est la géométrie des espaces affines : il s agit grossièrement d ensembles de points définis par des propriétés spécifiques permettant de parler d alignement, de parallélisme, d intersection. Les notions de longueur et d… … Wikipédia en Français
Géométrie affine — La géométrie affine est la géométrie des espaces affines : il s agit grossièrement d ensembles de points définis par des propriétés spécifiques permettant de parler d alignement, de parallélisme, d intersection. Les notions de longueur et d… … Wikipédia en Français
Segment (géométrie) — Segment (mathématiques) Pour les articles homonymes, voir segment. Un segment, en géométrie, est une portion de droite. Un segment reliant deux points A et B est noté [A,B] et représente la partie de la droite (AB) qui se situe… … Wikipédia en Français
Théorème de Carathéodory (géométrie) — Ne pas confondre avec le théorème d extension de Carathéodory. Le théorème de Carathéodory est un théorème de géométrie relatif aux enveloppes convexes dans le contexte des espaces affines de dimension finie. Sommaire 1 Énoncé … Wikipédia en Français
Théorème de carathéodory (géométrie) — Le théorème de Carathéodory est un théorème de géométrie relatif aux enveloppes convexes dans le contexte des espaces affines de dimension finie. Sommaire 1 Énoncé 2 Preuves 2.1 La preuve usuelle … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Barycentre (géométrie euclidienne)