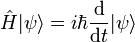ℏ

ℏ

Constante de Planck réduite

Cet article fait partie de la série
Mécanique quantique
\hat H | \psi\rangle = i\hbar\frac{{\rm d}}{{\rm d}t}|\psi\rangle
Postulats de la mécanique quantique

Histoire de la mécanique quantique

La constante de Planck réduite, ou constante de Dirac (du nom du physicien Paul Dirac), notée ℏ (prononcer « h barre »), est dérivée de la constante de Planck h. Le symbole ℏ correspond au caractère unicode U+210F[1].


Elle est conventionnellement définie par la formule :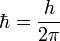

\hbar=\frac{h}{2\pi}.

Sa valeur numérique est de

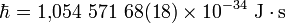\hbar =1,\!054\ 571\ 68(18)\times10^{-34}\ \mbox{J}\cdot\mbox{s} \,,

directement tirée de la constante de Planck, qui vaut :

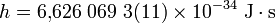h=6,\!626\ 069\ 3(11)\times10^{-34}\ \mbox{J}\cdot\mbox{s}.

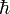\hbar est le quantum de moment angulaire, y compris le quantum de spin. C'est-à-dire que le moment angulaire de n'importe quel système, mesuré par rapport à n'importe quel choix particulier d'axe, est toujours un multiple entier de cette valeur. 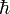\hbar est également utilisée dans le principe d'incertitude de Heisenberg. Pour cette raison, certains pensent que[réf. nécessaire] 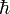\hbar est plus fondamental que h. 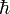\hbar est employé pour définir les unités de Planck.

Cette constante est (entre autres) utilisée dans :

Notes et références

Voir aussi

Articles connexes

  • Portail de la physique Portail de la physique
Ce document provient de « Constante de Planck r%C3%A9duite ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article ℏ de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”