Équipotence

Bijection assurant l'équipotence des deux ensembles de quatre éléments.

En mathématiques, l’équipotence est une relation entre ensembles, selon laquelle deux ensembles sont équivalents lorsqu'il existe une bijection entre eux. Cette notion permet de définir la cardinalité, c'est-à-dire le nombre d'éléments d'un ensemble, qu'il soit fini ou infini.

La subpotence est une relation plus faible, satisfaite lorsqu'il existe une injection entre deux ensembles. Elle permet de définir une comparaison de taille entre les ensembles, sans présupposer la construction des nombres cardinaux.

Définitions

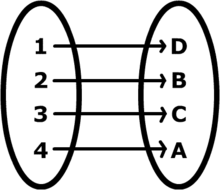
Deux ensembles E et F sont dits équipotents s'il existe une bijection de E sur F, c'est-à-dire une application pour laquelle tout élément de F admet un unique antécédent.

Un ensemble E est dit subpotent à un ensemble F s'il existe une injection de E dans F, c'est-à-dire une application pour laquelle tout élément de F ne peut avoir plusieurs antécédents..

Propriétés élémentaires

Tout ensemble est équipotent à lui-même puisque l'application identité est bijective. Par conséquent, la relation d'équipotence est réflexive.

La relation est aussi symétrique, puisque toute bijection de E sur F admet une réciproque qui est bijective également de F sur E.

Enfin, la relation est transitive, puisque deux bijections de E sur F et de F sur G peuvent être composées pour former une bijection de E sur G.

De même, la relation de subpotence est réflexive et transitive, mais pas symétrique : il existe une injection canonique du singleton {1} dans la paire {1 ; 2} mais il n'existe pas d'injection de {1 ; 2} dans {1}. En effet, il n'existe qu'une application de {1 ; 2} dans {1} et pour cette application les deux éléments 1 et 2 ont la même image 1.

Théorème de Cantor-Bernstein

Si deux ensembles sont subpotents l'un à l'autre, alors ils sont équipotents.

Application aux ensembles finis

Pour tout entier naturel n strictement positif, l'intervalle d'entiers {1,...,n} n'est subpotent à aucun intervalle d'entiers {1,...,p} où p est strictement inférieur à n.

Ce résultat se démontre par récurrence sur n.

L'initialisation est donnée en propriétés élémentaires.

Soit n un entier strictement positif tel que pour tout entier p compris entre 1 et n, l'intervalle d'entiers {1,...,n} n'est pas subpotent à {1,...,p}.

Soit p un entier compris entre 1 et n, et f une application de {1,...,n + 1} dans {1,...,p}.

• Si f(n + 1) appartient à l'image f({1,...,n}) alors f(n + 1) a deux antécédents donc f n'est pas injective.
• Si f(n + 1) n'appartient pas à l'image f({1,...,n}), alors l'entier p est au moins égal à 2 et il est possible de définir l'application g de {1,...,n} dans {1,...,p − 1} par :
  
  L'application g n'étant pas injective par hypothèse de récurrence, il existe y dans {1,...,p − 1} qui ait deux antécédents par g.
  • Si y est strictement inférieur à f(n + 1), alors y admet aussi deux antécédents par f.
  • Si y est supérieur ou égal à f(n + 1), alors (y + 1) admet aussi deux antécédents par f.

Finalement, f n'est pas injective.

Donc la propriété est démontrée au rang n + 1.

Comme en revanche tout intervalle d'entiers {1,...,p} est subpotent à {1,...,n} lorsque p est inférieur ou égal à n par injection canonique, il s'en déduit que deux intervalles d'entiers de la forme {1,...,n} et {1,...,p} sont équipotents si et seulement si n = p.

Sur la classe des ensembles

Ces propriétés de l'équipotence sont caractéristiques des relations d'équivalence, à la réserve près que la classe des ensembles ne constitue pas elle-même un ensemble. Il ne s'agit donc pas d'une relation au sens ensembliste du terme.

La classe d'équipotence d'un ensemble donné est une classe propre dès que cet ensemble est non vide (on construirait sinon par réunion un ensemble de tous les ensembles).

Par conséquent si l'on définit les cardinaux comme des classes d'équipotence, on a de fortes limitations sur leur maniement. Pas question de parler d'ensembles ni de classes de cardinaux. Ce ne sont tout simplement pas des objets des théories des ensembles à la ZFC.

La théorie des classes de von Neumann, Bernays et Gödel, dans laquelle les classes sont des objets de la théorie, alors que, dans ZFC, elles sont représentées par des prédicats, a cependant les mêmes limitations sur leur maniement, internalisées par l'axiomatisation de la théorie.

Une façon de remédier à cette situation est de construire de façon uniforme un représentant unique par classe d'équipotence. On utilise pour cela les ordinaux, un cardinal étant, selon une définition qui apparait déjà chez Georg Cantor, un ordinal qui n'est pas équipotent à un ordinal strictement plus petit. La définition des ordinaux pose cependant le même genre de problèmes (pour les classes d'isomorphie de bons ordres), et c'est John von Neumann qui en a donné la construction usuelle. cette définition nécessite le schéma d'axiomes de remplacement, et donc la théorie ZF, pour avoir suffisamment d'ordinaux, et l'axiome du choix, et donc finalement la théorie ZFC, pour qu'il y ait bien au moins un ordinal, et donc exactement un cardinal, dans chaque classe d'équipotence (on montre effet, grâce à l'axiome du choix, que tout ensemble est bien ordonné, et grâce au schéma de remplacement que tout bon ordre est isomorphe a un ordinal de von Neumann).

Il est cependant tout à fait possible de développer les aspects les plus élémentaires de la cardinalité en termes d'équipotence, tant que l'on s'intéresse par exemple à des comparaisons de cardinaux. L'équipotence fournit l'égalité des cardinaux. La subpotence — l'existence d'une injection d'une ensemble dans un autre — est compatible avec l'équipotence et la subpotence stricte — subpotent mais pas équipotent — également. Cela permet de définir égalité et ordre entre classes cardinales, sachant qu'au fond, il s'agit juste d'une « façon de parler » de l'équipotence et de la subpotence.

Voir aussi

• Bijection
• Isomorphisme
• Nombre cardinal
• Théorie naïve des ensembles

• Portail des mathématiques