- Équation de Murnaghan
-
Équation d'état de Murnaghan
L'équation d'état de Murnaghan est une équation d'état de la mécanique des milieux continus. Elle décrit l'évolution isotherme du volume d'un solide en fonction de la pression — un problème important en sciences de la terre. Cette équation fait intervenir trois paramètres, tous trois pris à température constante et à pression nulle : le volume V0, le module d'incompressibilité K0 et sa dérivée première par rapport à la pression K'0.
Cette équation fut publiée en 1944 par F.D. Murnaghan, en réaction à la publication de données expérimentales collectées jusqu'à 100 000 atmosphères (10 GPa) qui remettaient en cause la validité des équations usuelles (et notamment la loi de Hooke, déjà mise à mal). Ceci amène Murnaghan à tenir compte des variations de la compressibilité avec la pression[1]. Par la suite, d'autres auteurs ont proposé des généralisations de l'équation de Murnaghan (développement au second ordre ou plus, prise en compte de la température[2]).
Le domaine de validité de l'équation de Murnaghan reste toutefois limité car sa démonstration repose sur l'hypothèse des déformations infinitésimales[3]. L'expérience montre qu'elle reste à peu près valable tant que la compression V / V0 reste supérieure à 90% environ[4]. Dans cette gamme, elle présente l'intérêt d'offrir une expression explicite du volume en fonction de la pression V(P)[5]. Elle se distingue d'autres équations d'état établies par la suite (équation de Birch-Murnaghan, équation de Vinet…) qui s'appuient sur la théorie des grandes déformations mais donnent uniquement des expressions explicites de la pression en fonction du volume P(V).
Expression et démonstration
Le module d'incompressibilité et sa dérivée sont donnés par les expressions
et
On fait l'hypothèse que le module d'incompressibilité est une fonction linéaire de la pression :
L'équation de Murnaghan est le résultat de l'intégration de cette équation différentielle :
On peut ensuite exprimer le volume en fonction de la pression :
Notes et références
- ↑ (en) F.D. Murnaghan, « The Compressibility of Media under Extreme Pressures », dans Proceedings of the National Academy of Sciences of the United States of America, vol. 30, p. 244-247 [texte intégral]
- ↑ (en) G. E. Fernández, « A Debye-Grüneisen thermal correction to the Murnaghan equation of state of solids », dans Journal of Physics and Chemistry of Solids, vol. 59, 1998, p. 867-870 [texte intégral]
- ↑ (en) Kazuhiro Fuchizaki, « Murnaghan equation of state revisited », dans Journal of the Physical Society of Japan, vol. 75, 2006, p. 034601 [texte intégral]
- ↑ (en) R.J. Angel, High-Pressure Crystallography, « Some pratical aspects of studying equations of state and structural phase transitions at high pressure », p. 21-36
- ↑ (en) W.B. Holzapfel, « Physics of solids under strong compression », dans Reports on Progress in Physics, vol. 59, 1996, p. 29-90 [texte intégral]
- Portail de la physique
Catégorie : Physique du solide
Wikimedia Foundation. 2010.

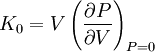
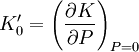
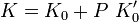
![P(V) = \frac{K_0}{K_0'} \left[\left(\frac{V}{V_0}\right)^{-K_0'} - 1\right]](/pictures/frwiki/53/596890cb79374e281b379a2c904ae721.png)
![V(P) = V_0 \left[1+ P \left(\frac{K'_0}{K_0}\right)\right]^{-1/K'_0}](/pictures/frwiki/51/38fcafdbca7175774993e03affbb4b39.png)