Équation de Birch-Murnaghan
- Équation de Birch-Murnaghan
-
Équation d'état de Birch-Murnaghan
L'équation d'état de Birch-Murnaghan est une équation d'état utilisée en mécanique des milieux continus. Elle décrit l'évolution isotherme du volume d'un solide en fonction de la pression.
Cette équation fait intervenir trois paramètres, tous trois pris à température constante : le volume à pression nulle V0, le module de compressibilité noté ici K0 et sa dérivée première par rapport à la pression K0'. Ces deux derniers sont donnés respectivement par
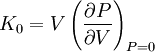
et
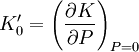
L'équation de Birch-Murnaghan est à distinguer de l'équation d'état de Murnaghan, également très utilisée en sciences de la terre et en physique de la matière condensée. Cette dernière n'est en effet valable que pour des déformations infinitésimales alors que la première repose sur la théorie des grandes déformations[1]. Sa démonstration repose sur un développement en série de l'énergie libre en fonction de la mesure d'Euler de la déformation notée f et donnée par
![f = \frac{1}{2}\left[\left(\frac{V}{V_0}\right)^{-\frac{2}{3}} - 1\right]](/pictures/frwiki/50/25c2fab70d6ec45e2d057b26d45a33a1.png)
On utilise couramment l'équation au troisième ordre qui s'écrit
![P = \frac{3}{2} K_0 \left[\left(\frac{V}{V_0}\right)^{-\frac{7}{3}} - \left(\frac{V}{V_0}\right)^{-\frac{5}{3}}\right]\left[1 + \frac{3}{4}\left(K_0' - 4\right)\left[\left(\frac{V}{V_0}\right)^{-\frac{2}{3}}-1\right]\right]](/pictures/frwiki/53/57ca051d745879641ffb33ebb1a1335c.png)
Au second ordre, on a K0' = 4 et l'expression précédente est amputée de son dernier facteur.
Cette relation peut être utilisée pour estimer les coefficients K0 et K'0 à partir de mesures du volume en fonction de la pression, notamment par diffraction des rayons X. Le tableau suivant donne quelques exemples de matériaux étudiés de cette façon à température ambiante.
Notes et références
- ↑ (en) Kazuhiro Fuchizaki, « Murnaghan equation of state revisited », dans Journal of the Physical Society of Japan, vol. 75, 2006, p. 034601 [texte intégral]
- ↑ a et b (en) J. B. Burt, N. L. Ross, R. J. Angel and Mario Koch, « Equations of state and structures of andalusite to 9.8 GPa and sillimanite to 8.5 GPa », dans American mineralogist, vol. 91, 2006, p. 319
- ↑ (en) C. E. Runge, A. Kubo, B. Kiefer, Y. Meng, V. B. Prakapenka, G. Shell, R. J. Cava, T. S. Duffy, « Equation of state of MgGeO3 perovskite to 65 GPa : comparison with the post-perovskite phase », dans Physics and chemistry of minerals, vol. 33, 2006, p. 699-709
Sources
- (en) F. Birch, « Finite elastic strains of cubic crystals », dans Physical Review, vol. 71, 1947, p. 809 [texte intégral]
 Portail de la physique
Portail de la physique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Équation de Birch-Murnaghan de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Équation d'état de Birch-Murnaghan — Ne doit pas être confondu avec Équation d état de Murnaghan. L équation d état de Birch Murnaghan est une relation qui lie le volume d un corps et la pression à laquelle il est soumis. C est une des nombreuses équations d état qui ont été… … Wikipédia en Français
Birch–Murnaghan equation of state — In continuum mechanics, an equation of state suitable for modeling solids is naturally rather different from the ideal gas law. A solid has a certain equilibrium volume V0, and the energy increases quadratically as volume is increased or… … Wikipedia
Équation de Murnaghan — Équation d état de Murnaghan L équation d état de Murnaghan est une équation d état de la mécanique des milieux continus. Elle décrit l évolution isotherme du volume d un solide en fonction de la pression un problème important en sciences de la… … Wikipédia en Français
Équation d'état de Murnaghan — Ne doit pas être confondu avec Équation d état de Birch Murnaghan. L équation d état de Murnaghan est une relation qui lie le volume d un corps et la pression à laquelle il est soumis. C est une des nombreuses équations d état qui ont été… … Wikipédia en Français
Equation d'etat — Équation d état En thermodynamique, une équation d état d un système à l équilibre thermodynamique est une relation entre différents paramètres physiques (appelés variables d état) qui déterminent son état. Il peut s agir par exemple d une… … Wikipédia en Français
Équation d’état — Équation d état En thermodynamique, une équation d état d un système à l équilibre thermodynamique est une relation entre différents paramètres physiques (appelés variables d état) qui déterminent son état. Il peut s agir par exemple d une… … Wikipédia en Français
Murnaghan — may refer to: Dermot Murnaghan (born 1957), journalist and television presenter Francis Dominic Murnaghan (mathematician) (1873–1976) Francis Dominic Murnaghan, Jr. (1920–2000), judge George Murnaghan (1847–1929), politician Sheelagh Murnaghan… … Wikipedia
Équation d'état — En physique, et plus particulièrement en thermodynamique, une équation d état d un système à l équilibre thermodynamique est une relation entre différents paramètres physiques (appelés variables d état) qui déterminent son état. Il peut s agir… … Wikipédia en Français
Francis Birch (geophysicist) — Albert Francis Birch (22 August 1903 30 January 1992) was the Sturgis Hooper Professor of Geology at Harvard University from 1949 to 1974. A geophysicist best known for his experimental work on the properties of Earth forming minerals at high… … Wikipedia
Francis Dominic Murnaghan — (1873 1976) est un mathématicien irlandais. Il a réalisé sa carrière à l université Johns Hopkins aux États Unis. Son nom est associé à des développements en théorie des groupes, ainsi qu en mathématiques appliquées à la mécanique des milieux… … Wikipédia en Français

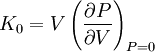
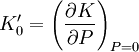
![f = \frac{1}{2}\left[\left(\frac{V}{V_0}\right)^{-\frac{2}{3}} - 1\right]](/pictures/frwiki/50/25c2fab70d6ec45e2d057b26d45a33a1.png)
![P = \frac{3}{2} K_0 \left[\left(\frac{V}{V_0}\right)^{-\frac{7}{3}} - \left(\frac{V}{V_0}\right)^{-\frac{5}{3}}\right]\left[1 + \frac{3}{4}\left(K_0' - 4\right)\left[\left(\frac{V}{V_0}\right)^{-\frac{2}{3}}-1\right]\right]](/pictures/frwiki/53/57ca051d745879641ffb33ebb1a1335c.png)