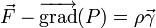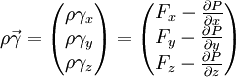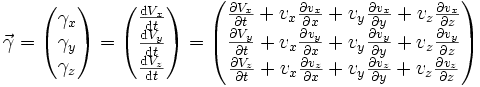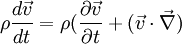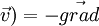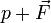Équation d'Euler
- Équation d'Euler
-
Équations d'Euler
L'équation d'Euler (établie par Euler en 1755) s'applique dans le cas d'un fluide parfait, c’est-à-dire un fluide non visqueux et sans conductivité thermique. Le fluide peut être incompressible ou compressible. Complétée par d'autres équations tirées de la dynamique des fluides parfaits, elle permet de caractériser un mouvement du fluide en calculant par exemple sa pression motrice.
Une intégration le long d'une ligne de courant de cette équation permet d'obtenir l'équation de Bernoulli.
L'équation d'Euler dérive de la relation fondamentale de la dynamique, appliquée à une particule fluide :
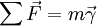
Faisons le bilan des forces appliquées à un élément de volume :
- les forces de volume
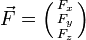 , proportionnelles à l'élement de volume considéré ;
, proportionnelles à l'élement de volume considéré ;
- les forces de pression, proportionnelles à l'élement de surface considéré ;
- les forces d'inertie, proportionnelles à l'accélération
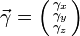 et au volume du fluide ;
et au volume du fluide ;
on obtient donc :
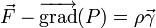
C'est la forme condensée de l'équation d'Euler.
En développant, on a :
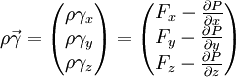
Une autre forme de l'équation d'Euler (les équations, dans ce cas) s'écrit :
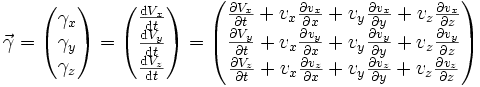
c'est à dire, 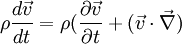
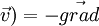
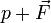
 Portail de la physique
Portail de la physique
Catégorie : Mécanique des fluides
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Équation d'Euler de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
équation d’Euler — Oilerio lygtis statusas T sritis fizika atitikmenys: angl. Euler equation vok. Eulersche Gleichung, f rus. уравнение Эйлера, n pranc. équation d’Euler, f … Fizikos terminų žodynas
Equation d'Euler-Lagrange — Équation d Euler Lagrange Pour les articles homonymes, voir Lagrange. L’équation d Euler Lagrange est un résultat mathématique qui joue un rôle fondamental dans le calcul des variations. On retrouve cette équation dans de nombreux problèmes réels … Wikipédia en Français
Équation d'euler-lagrange — Pour les articles homonymes, voir Lagrange. L’équation d Euler Lagrange est un résultat mathématique qui joue un rôle fondamental dans le calcul des variations. On retrouve cette équation dans de nombreux problèmes réels de minimisation de… … Wikipédia en Français
Équation d'Euler-Lagrange — Pour les articles homonymes, voir Lagrange. L’équation d Euler Lagrange est un résultat mathématique qui joue un rôle fondamental dans le calcul des variations. On retrouve cette équation dans de nombreux problèmes réels de minimisation de… … Wikipédia en Français
Euler-Bernoulli beam equation — Euler Bernoulli beam theory, or just beam theory, is a simplification of the linear theory of elasticity which provides a means of calculating the load carrying and deflection characteristics of beams. It was first enunciated circa 1750, but was… … Wikipedia
Equation differentielle d'Euler — Équation différentielle d Euler En mathématiques, l équation d Euler est une équation différentielle linéaire de la forme suivante Elle peut être ramenée par changement de variable à une équation différentielle linéaire à coefficients constants.… … Wikipédia en Français
Équation différentielle d'euler — En mathématiques, l équation d Euler est une équation différentielle linéaire de la forme suivante Elle peut être ramenée par changement de variable à une équation différentielle linéaire à coefficients constants. Pour appliquer la théorie… … Wikipédia en Français
Équation différentielle d'Euler — En mathématiques, l équation d Euler est une équation différentielle linéaire de la forme suivante Elle peut être ramenée par changement de variable à une équation différentielle linéaire à coefficients constants. Pour appliquer la théorie… … Wikipédia en Français
Euler — Leonhard Euler « Euler » redirige ici. Pour les autres significations, voir Euler (homonymie). Leonhard Euler … Wikipédia en Français
Euler equation — Oilerio lygtis statusas T sritis fizika atitikmenys: angl. Euler equation vok. Eulersche Gleichung, f rus. уравнение Эйлера, n pranc. équation d’Euler, f … Fizikos terminų žodynas
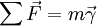
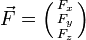 , proportionnelles à l'élement de volume considéré ;
, proportionnelles à l'élement de volume considéré ;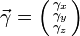 et au volume du fluide ;
et au volume du fluide ;