Échantillonnage d'importance

Échantillonnage d'importance

Échantillonnage préférentiel

L'échantillonnage préférentiel, en anglais importance sampling, est une méthode de réduction de la variance qui peut être utilisée dans la méthode de Monte-Carlo. L'idée sous-jacente à l'échantillonnage préférentiel, EP dans la suite, est que certaines valeurs prises par une variable aléatoire dans une simulation ont plus d'impact que d'autres sur l'estimateur recherché. Si ces valeurs importantes se réalisent plus souvent, la variance de notre estimateur peut être réduite. Par conséquent la méthodologie de l'EP est de choisir une distribution qui « encourage » les valeurs importantes. L'utilisation d'une distribution biaisée conduira à un estimateur biaisé si nous l'appliquons directement aux simulations. Cependant, les différentes simulations sont pondérées afin de corriger ce biais, l'estimateur EP est alors sans biais. Le poids qui est donné à chaque simulation est le ratio de vraisemblance, qui est la densité de Radon-Nikodym de la vraie distribution par rapport à la distribution biaisée.

Le point fondamental dans l'implémentation d'une simulation utilisant l'EP est le choix de la distribution biaisée. Choisir ou créer une bonne distribution biaisée est l'art des EP. L'avantage peut alors être une énorme économie de temps de calculs alors que l'inconvénient pour une mauvaise distribution peut être des calculs plus longs qu'une simple simulation de Monte-Carlo.

Sommaire

Approche Mathématique

Principe général

La méthode de Monte-Carlo classique

Article détaillé : Méthode de Monte-Carlo.

On souhaite estimer une quantité G, qui s'exprime sous la forme d'une intégrale :

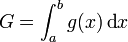
G = \int_a^b g(x) \,\mbox{d}x

On considère ici une intégration en dimension 1, mais on peut généraliser à une dimension quelconque.

Le principe de base des méthodes de Monte-Carlo est de voir l'intégrale précédente comme

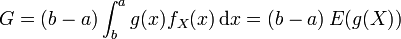
G = (b-a)\int^a_b g(x) f_X(x) \,\mbox{d}x = (b-a)\,E(g(X))

où X est une variable aléatoire uniformément distribuée sur [a;b] et 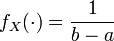f_X(\cdot)=\frac{1}{b-a} sa densité.

Si on dispose d'un échantillon 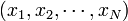(x_1, x_2, \cdots, x_N), identiquement et indépendamment distribué (i.i.d.) selon U([a;b]), on peut estimer G par :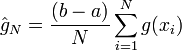

\hat{g}_N = \frac{(b-a)}{N} \sum_{i=1}^N g(x_i)

Il s'agit, d'après la loi des grands nombres, d'un estimateur de G non-biaisé (c'est-à-dire que 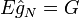E \hat{g}_N= G). Sa variance est :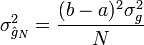

\sigma^2_{\hat{g}_N} = \frac{(b-a)^2\sigma^2_g}{N}

avec 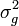\sigma^2_g la variance de la variable aléatoire g(X)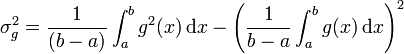

\sigma^2_g =\frac{1}{(b-a)}\int_a^b g^2(x) \,\mbox{d}x - \left(\frac{1}{b-a}\int_a^b g(x) \,\mbox{d}x\right)^2

L'échantillonnage préférentiel

L'idée principale de l'échantillonnage préférentiel est de remplacer dans la simulation la densité uniforme sur [a;b] par une densité alternative (ou densité biaisée), disons 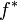f^{\ast}\,, qui tente d'imiter la fonction g. Ce faisant, on remplace les tirages uniformes, qui n'avantagent aucune région, par des tirages plus « fidèles ». Ainsi, l'échantillonnage est fait suivant l'importance de la fonction g: il est inutile de tirer dans les régions où g prend des valeurs non-significatives, pour, au contraire, se concentrer sur les régions de haute importance. On espère ainsi diminuer la variance 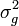\sigma^2_g. Autrement dit, si on se fixe un niveau d'erreur donné, l'EP permet de diminuer théoriquement le nombre de simulations N par rapport à une méthode de Monte-Carlo classique.

L'intégrale à estimer est ré-écrite comme:

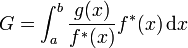
G = \int_a^b \frac{g(x)}{f^{\ast}(x)} f^{\ast}(x) \, \mbox{d}x

ce qui revient à:

G = E^{\ast} [w(X)]

où on a posé 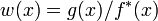w(x)=g(x)/f^{\ast}(x) (appelé ratio de vraisemblance) et où X est simulé selon la densité 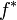f^{\ast}. Il est facile de généraliser les résultats précédents: l'estimateur de G est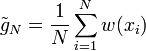

\tilde{g}_N = \frac{1}{N} \sum_{i=1}^N w(x_i)

où 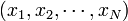(x_1, x_2, \cdots, x_N) est un échantillon i.i.d. selon la densité 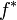f^{\ast}. La variance de l'estimateur est donné par

\mbox{Var}^{\ast} (\tilde{g}_N) = \frac{\mbox{Var}^{\ast}[w(X)]}{N}

avec enfin

\mbox{Var}^{\ast}[w(X)] = \mbox{Var}^{\ast}\left[\frac{g(X)}{f^{\ast}(X)}\right]=\int_a^b \left[\frac{g(x)}{f^{\ast}(x)}\right]^2 f^{\ast}(x) \,\mbox{d}x - G^2

Dès lors, le problème est de se concentrer sur l'obtention d'une densité biaisée 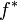f^{\ast}\, telle que la variance de l'estimateur EP soit moindre que celle de la méthode de Monte-Carlo classique. La densité minimisant la variance (qui la rend nulle sous certaines conditions) est appelée densité biaisée optimale. Cette dernière est égale à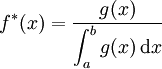

f^{\ast}(x) = \frac{g(x)}{\displaystyle \int_a^b g(x) \,\mbox{d}x}

mais ce choix est inopérant, car on recherche justement le dénominateur. Mais, on peut s'attendre à réduire la variance en choisissant une densité 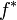f^{\ast} reproduisant la fonction g.

Application: estimation d'une probabilité

Considérons que nous voulons estimer par simulation la probabilité 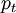p_t\, d'un événement 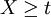{ X \ge t\ } où X est une variable aléatoire de fonction de distribution F et de densité 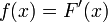f(x)= F'(x)\,. Ce problème se ramène à la présentation générale dans le sens où il met en œuvre une intégrale à estimer. Un échantillon 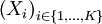\left(X_i\right)_{i \in\{1,\dots,K\}} identiquement et indépendamment distribué (i.i.d.) est tiré dans cette loi. On note kt le nombre de réalisation supérieures à t. La variable kt est une variable aléatoire suivant une loi binomiale de paramètres K et pt: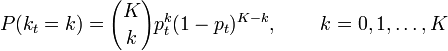

P(k_t = k)={K\choose k}p_t^k(1-p_t)^{K-k},\,\quad \quad k=0,1,\dots,K

ce qui signifie notamment que E(kt) = Kpt: la fréquence empirique kt / N converge donc vers sa probabilité associée pt.

L'échantillonnage préférentiel entre en jeu ici pour diminuer la variance de l'estimation Monte-Carlo de la probabilité 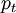p_t\,. En effet, 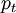p_t\, est donnée par

\begin{align} p_t &= {E} [X \ge t]\\ &= \int (x \ge t) \frac{f(x)}{f^{\ast}(x)} f^{\ast}(x) \,dx\\ &= {E_*} [(X \ge t) w(X)] \end{align}

où, on a encore posé

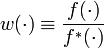
w(\cdot) \equiv \frac{f(\cdot)}{f^{\ast}(\cdot)}

La dernière égalité de l'équation précédente suggère l'estimateur de pt suivant :

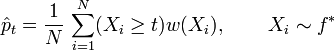
\hat p_t = \frac{1}{N}\,\sum_{i=1}^N (X_i \ge t) w(X_i),\,\quad \quad X_i \sim f^{\ast}

C'est un estimateur EP de 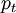p_t\, qui est sans biais. Ceci étant défini, la procédure d'estimation est de générer un échantillon i.i.d. à partir de la densité 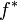f^{\ast}\, et pour chaque réalisation dépassant 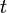t\, de calculer son poids 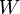W\,. Le résultat sera la moyenne obtenue avec 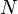N\, tirages. La variance de cet estimateur est :

\begin{align} \mbox{Var}^{\ast} \hat p_t &= \frac{1}{N} \mbox{Var}^{\ast} [(X \ge t)w(X)]\\ &= \frac{1}{N} \mbox{Var}^{\ast} [(X \ge t)w(X)] \\ &= \frac{1}{N}\Big[{E_*}[(X \ge t)^2 w^2(X)] - p_t^2 \Big]\\ &= \frac{1}{N}\Big[{E}[(X \ge t)^2 w(X)] - p_t^2 \Big] \end{align}

Là encore il faudra profile au mieux la densité 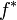f^{\ast} afin de diminuer la variance.

Un exemple numérique

On souhaite estimer la quantité suivante:

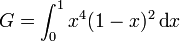
G = \int_0^1 x^4 (1-x)^2 \,\mbox{d}x

qui se trouve être la fonction bêta de paramètre (5;3), qui vaut G = 1/105 = 0,0095238095238095. Cela correspond au cas général avec a=0, b=1 et g(x) = x4(1 − x)2.

On simule un échantillon 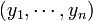(y_1, \cdots, y_n) selon la loi uniforme standard (U[0;1]) pour obtenir l'estimateur Monte-Carlo classique: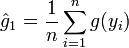

\hat{g}_1 = \frac{1}{n} \sum_{i=1}^n g(y_i)

et l'estimateur de sa variance:

\hat{\sigma}^2_{g_1} = \frac{1}{n} \left[ \frac{1}{n} \sum_{i=1}^n g^2(y_i) - \hat{g}_1^2\right]

S'inspirant de la forme générale de la fonction bêta, on peut remplacer la loi uniforme standard par la loi triangulaire T(a=0,c=2/3,b=1). Elle ressemble à un triangle basé sur le segment [0;1] et "culminant" en (2/3;2). Sa densité est

f^{\ast}(x) = \begin{cases} 3x & x \in [0;2/3]\\ 6(1-x) & x \in [2/3;1] \end{cases}

On simule un échantillon 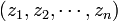(z_1, z_2, \cdots, z_n) dans cette loi, par la méthode de la transformée inverse, et, en posant 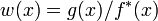w(x) = g(x)/f^{\ast}(x), l'estimateur EP est donné par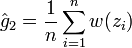

\hat{g}_2 = \frac{1}{n} \sum_{i=1}^n w(z_i)

et l'estimateur de sa variance est

\hat{\sigma}^2_{g_2} = \frac{1}{n} \left[ \frac{1}{n} \sum_{i=1}^n w^2(z_i) - \hat{g}_2^2\right]

Dans le tableau, on constate que l'utilisation de l'EP permet systématiquement de réduire la variance de l'estimation par rapport à l'estimation Monte-Carlo de même taille (c'est-à-dire à n donné). On constate aussi que la variance d'estimation est proportionnelle à 1/n: en passant de n = 1000 à n = 10 000 (multiplication par 10 dela taille), on réduit d'un facteur 10 la variance.


Comparaison de la méthode Monte-Carlo et de l'échantillonnage préférentiel
Monte-Carlo classique Echantillonage préférentiel
n estimateur biais variance estimateur biais variance
500 0,009843 -3,19E-004 1,32E-007 0,009712 -1,88E-004 2,50E-008
1000 0,009735 -2,12E-004 6,53E-008 0,009680 -1,57E-004 1,26E-008
2500 0,009628 -1,04E-004 2,60E-008 0,009576 -5,18E-005 5,36E-009
5000 0,009717 -1,93E-004 1,31E-008 0,009542 -1,83E-005 2,71E-009
10000 0,009634 -1,10E-004 6,52E-009 0,009544 -1,99E-005 1,35E-009

On espère améliorer encore les performances en considérant une densité 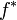f^\ast "plus proche" de la densité f. Le principal problème sera d'obtenir des simulations. Dans les cas les plus simples, comme la loi triangulaire, la méthode de la transformée inverse pourra suffir; dans les cas plus complexes, il faudra avoir recours à la méthode de rejet.

Voir aussi

Liens internes

Ce document provient de « %C3%89chantillonnage pr%C3%A9f%C3%A9rentiel ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Échantillonnage d'importance de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Echantillonnage d'importance — Échantillonnage préférentiel L échantillonnage préférentiel, en anglais importance sampling, est une méthode de réduction de la variance qui peut être utilisée dans la méthode de Monte Carlo. L idée sous jacente à l échantillonnage préférentiel,… …   Wikipédia en Français

  • Importance Sampling — Échantillonnage préférentiel L échantillonnage préférentiel, en anglais importance sampling, est une méthode de réduction de la variance qui peut être utilisée dans la méthode de Monte Carlo. L idée sous jacente à l échantillonnage préférentiel,… …   Wikipédia en Français

  • Importance sampling — Échantillonnage préférentiel L échantillonnage préférentiel, en anglais importance sampling, est une méthode de réduction de la variance qui peut être utilisée dans la méthode de Monte Carlo. L idée sous jacente à l échantillonnage préférentiel,… …   Wikipédia en Français

  • Échantillonnage préférentiel — L échantillonnage préférentiel, en anglais importance sampling, est une méthode de réduction de la variance qui peut être utilisée dans la méthode de Monte Carlo. L idée sous jacente à l échantillonnage préférentiel, EP dans la suite, est que… …   Wikipédia en Français

  • ÉCHANTILLON ET ÉCHANTILLONNAGE — ÉCHANTILLON & ÉCHANTILLONNAGE Le problème de la construction d’un échantillon se pose lorsqu’on n’a pas les moyens d’observer l’ensemble des personnes ou l’ensemble des situations auxquelles on s’intéresse. On appelle «population» cet ensemble… …   Encyclopédie Universelle

  • Filtre Particulaire (Statistique) — Pour les articles homonymes, voir Particule. Résultat d un filtrage particulaire (courbe rouge) basé sur les données observées génér …   Wikipédia en Français

  • Filtre Particulaire (statistique) — Pour les articles homonymes, voir Particule. Résultat d un filtrage particulaire (courbe rouge) basé sur les données observées génér …   Wikipédia en Français

  • Filtre particulaire (statistique) — Pour les articles homonymes, voir Particule. Résultat d un filtrage particulaire (courbe rouge) basé sur les données observées génér …   Wikipédia en Français

  • Filtre particulaire — Pour les articles homonymes, voir Particule. Résultat d un filtrage particulaire (courbe rouge) basé sur les données observées générées depuis la courbe bleue. Les filtres particulaires …   Wikipédia en Français

  • Variable régionalisée — La VR comme phénomène physique : topographie de la ville de Binche …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”