- Filtre particulaire (statistique)
-
Filtre particulaire (statistique)
 Pour les articles homonymes, voir Particule.
Pour les articles homonymes, voir Particule.Les filtres particulaires, aussi connus comme Méthodes de Monte-Carlo séquentielles, sont des techniques sophistiquées d'estimation de modèles basées sur la simulation.
Les filtres particulaires sont généralement utilisés pour estimer des modèles Bayésiens et constituent les méthodes 'en-ligne' analogues aux Méthodes de Monte-Carlo par Chaînes de Markov qui elles sont des méthodes 'hors-ligne' (donc a posteriori) et souvent similaires aux méthodes d'échantillonnage d'importance.
S'ils sont conçus correctement, les filtres particulaires peuvent être plus rapides que les Méthodes de Monte-Carlo par Chaînes de Markov. Ils constituent souvent une alternative aux filtres de Kalman étendus avec l'avantage qu'avec suffisamment d'échantillons, ils approchent l'estimé Bayésien optimal. Ils peuvent donc être rendus plus précis que les filtres de Kalman. Les approches peuvent aussi être combinées en utilisant un filtre de Kalman comme une proposition de distribution pour le filtre particulaire.
Sommaire
Objectif
Un filtre particulaire a pour but d'estimer la séquence de paramètres cachés, xk pour
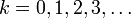 en se basant seulement sur les données observées yk pour
en se basant seulement sur les données observées yk pour 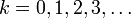 . Tous les paramètres estimés bayésiens de xk viennent de la distribution a posteriori, mais plutôt que d'utiliser les probabilités jointes a posteriori
. Tous les paramètres estimés bayésiens de xk viennent de la distribution a posteriori, mais plutôt que d'utiliser les probabilités jointes a posteriori 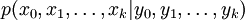 , qui résulteraient d'une MCMC usuelle ou d'un échantillonnage d'importance, les méthodes particulaires estiment la distribution de filtrage
, qui résulteraient d'une MCMC usuelle ou d'un échantillonnage d'importance, les méthodes particulaires estiment la distribution de filtrage 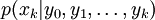 .
.Modélisation
Les filtres particulaires font l'hypothèse que les états xk et les observations yk peuvent être modélisées sous la forme suivante :
- La suite des paramètres
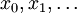 forment une chaîne de Markov de premier ordre, telle que
forment une chaîne de Markov de premier ordre, telle que 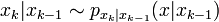 et avec une distribution initiale p(x0).
et avec une distribution initiale p(x0). - Les observations
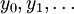 sont indépendantes conditionnellement sous réserve que les
sont indépendantes conditionnellement sous réserve que les 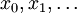 soient connus. En d'autres termes, chaque observation yk ne dépend que du paramètre xk :
soient connus. En d'autres termes, chaque observation yk ne dépend que du paramètre xk : 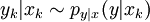
Un exemple de ce scénario est
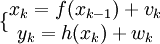
où à la fois vk et wk sont des séquences mutuellement indépendantes et distribuées à l'identique avec des fonctions de densité de probabilité connues et où f() et h() sont des fonctions connues. Ces deux équations peuvent être vues comme des équations de l'espace d'état et ressemblent à celles du filtre de Kalman.
Si les fonctions
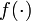 et
et 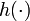 étaient linéaires, et si à la fois vk et wk étaient des gaussiennes, alors le filtre de Kalman trouve la distribution de filtrage bayésien exacte. Dans le cas contraire, les méthodes à base de filtre de Kalman donnent une estimation de premier ordre. Les filtres particulaires donnent également des approximations, mais avec suffisamment de particules, les résultats peuvent être encore plus précis.
étaient linéaires, et si à la fois vk et wk étaient des gaussiennes, alors le filtre de Kalman trouve la distribution de filtrage bayésien exacte. Dans le cas contraire, les méthodes à base de filtre de Kalman donnent une estimation de premier ordre. Les filtres particulaires donnent également des approximations, mais avec suffisamment de particules, les résultats peuvent être encore plus précis.Approximation de Monte-Carlo
Les méthodes à particules, comme toutes les méthodes à base d'échantillonnages (telles que les MCMC), génèrent un ensemble d'échantillons qui approximent la distribution de filtrage
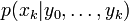 . Ainsi, avec P échantillons, les valeurs espérées vis-à-vis de la distribution de filtrage sont approximées par :
. Ainsi, avec P échantillons, les valeurs espérées vis-à-vis de la distribution de filtrage sont approximées par : 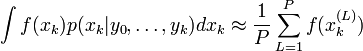 où
où 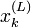 est la (L)-ième particule à l'instant k; et
est la (L)-ième particule à l'instant k; et 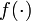 , de la façon habituelle des méthodes Monte-Carlo, peut donner tous les données de la distribution (moments, etc.) jusqu'à un certain degré d'approximation.
, de la façon habituelle des méthodes Monte-Carlo, peut donner tous les données de la distribution (moments, etc.) jusqu'à un certain degré d'approximation.En général, l'algorithme est répété itérativement pour un nombre donné de valeurs k (que nous noterons N).
Initialiser xk = 0 | k = 0 pour toutes les particules fournit une position de départ pour générer x1, qui peut être utilisé pour générer x2, qui peut être utilisé pour générer x3, et ainsi de suite jusqu'à k = N.
Une fois ceci effectué, la moyenne des xk sur toutes les particules (ou
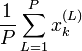 ) est approximativement la véritable valeur de xk.
) est approximativement la véritable valeur de xk.Echantillonnage avec rééchantillonnage par importance (SIR)
L'échantillonnage avec rééchantillonnage par importance (Sampling Importance Resampling ou SIR) est un algorithme de filtrage utilisé très couramment. Il approxime la distribution de filtrage
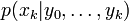 par un ensemble de particules pondérées :
par un ensemble de particules pondérées : 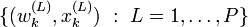 .
.Les poids d'importance
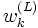 sont des approximations des probabilités (ou des densités) a posteriori relatives des particules telles que
sont des approximations des probabilités (ou des densités) a posteriori relatives des particules telles que 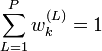 .
.L'algorithme SIR est une version récursive de l'échantillonnage par importance. Comme en échantillonnage par importance, l'espérée de la fonction
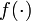 peut être approximé comme une moyenne pondérée :
peut être approximé comme une moyenne pondérée : 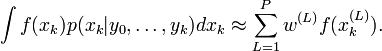
La performance de l'algorithme est dépendante du choix des distributions d'importances : π(xk | x0:k − 1,y0:k).
La distribution d'importance optimale est donnée comme : π(xk | x0:k − 1,y0:k) = p(xk | xk − 1,yk).
Cependant, la probabilité de transition est souvent utilisée comme fonction d'importance, comme elle est plus aisée de calculer, et cela simplifie également les calculs des poids d'importance subséquents : π(xk | x0:k − 1,y0:k) = p(xk | xk − 1).
Les filtres à rééchantillonnage par importance (SIR) avec des probabilités de transitions comme fonction d'importance sont connues communément comme filtres à amorçage (bootstrap filters) ou algorithme de condensation.
Le rééchantillonnage permet d'éviter le problème de la dégénérescence de l'algorithme. On évite ainsi les situations où tous les poids d'importance sauf un sont proches de zéro. La performance de l'algorithme peut aussi être affectée par le choix de la méthode de rééchantillonnage appropriée. Le rééchantillonnage stratifié proposé par Kitagawa (1996) est optimal en termes de variance.
Un seul pas de rééchantillonnage d'importance séquentiel se déroule de la façon suivante :
- Pour
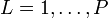 , on tire les échantillons des distributions d'importances :
, on tire les échantillons des distributions d'importances : 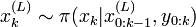
- Pour
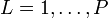 , on évalue les poids d'importance avec une constante de normalisation:
, on évalue les poids d'importance avec une constante de normalisation: 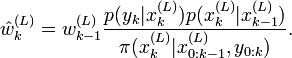
- Pour
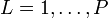 on calcule les poids d'importance normalisés:
on calcule les poids d'importance normalisés: 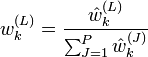
- On calcule une estimation du nombre effectif de particules comme
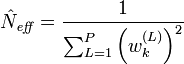
- Si le nombre effectif de particules est plus petit qu'un seuil donné
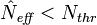 , alors on effectue le rééchantillonnage:
, alors on effectue le rééchantillonnage:
- Tirer P particules de l'ensemble de particules courant avec les probabilités proportionnelles à leur poids puis remplacer l'ensemble des particules courantes avec ce nouvel ensemble.
- Pour
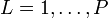 l'ensemble
l'ensemble 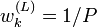 .
.
Le terme Rééchantillonnage d'importance séquentiel (Sequential Importance Resampling) est aussi utilisé parfois pour se référer aux filtres SIR.
Echantillonnage séquentiel par importance (SIS)
L'Echantillonnage séquentiel par importance (ou SIS pour Sequential Importance Sampling) est similaire à l'Echantillonnage avec rééchantillonage par importance (SIR) mais sans l'étape de rééchantillonnage.
Version directe de l'algorithme
La version directe de l'algorithme est relativement simple en comparaison des autres algorithmes de filtrage particulaire et utilise la composition et le rejet. Pour générer un simple échantillon x à k de
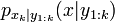 :
:- (1) Fixer p=1
- (2) Générer uniformémént L depuis {1,...,P}
- (3) Générer un test
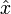 depuis sa distribution
depuis sa distribution 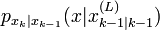
- (4) Générer les probabilités de
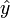 en utilisant
en utilisant 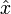 depuis
depuis 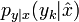 où yk est la valeur mesurée
où yk est la valeur mesurée - (5) Générer une autre uniformémént u depuis [0,mk]
- (6) Comparer u et
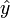
- (a) Si u est plus grand alors répéter depuis l'étape (2)
- (b) Si u est plus petite alors sauver
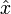 comme xk | k(p) et incrémenter p
comme xk | k(p) et incrémenter p - (c) Si p > P alors arrêter
L'objectif est de générer P particules au pas k en n'utilisant seulement que les particules du pas k − 1. Cela requiert qu'une équation markovienne puisse être écrite (et calculée) pour générer un xk en se basant seulement sur xk − 1. Cet algorithme utilise la composition de P particules depuis k − 1 pour générer à k.
Cela peut être plus facilement visualisé si x est vu comme un tableau à deux dimensions. Une dimension est k et l'autre dimension correspond au nombre de particules. Par exemple, x(k,L) serait la Lème particule à l'étape k et peut être donc écrite
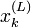 (comme effectué plus haut dans l'algorithme).
(comme effectué plus haut dans l'algorithme).L'étape (3) génère un potentiel xk basé sur une particule choisie aléatoirement (
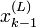 ) a temps k − 1 et rejette ou accepte cette particule à l'étape (6). En d'autres termes, les xk valeurs sont générées en utilisant les xk − 1 générées précédemment.
) a temps k − 1 et rejette ou accepte cette particule à l'étape (6). En d'autres termes, les xk valeurs sont générées en utilisant les xk − 1 générées précédemment.Voir aussi
- filtre de Kalman, un estimateur analytique pour les distributions Gaussiennes
- estimation récursive bayésienne
Références
- Sequential Monte Carlo Methods in Practice, par A Doucet, N de Freitas et N Gordon. Publié par Springer.
- On Sequential Monte Carlo Sampling Methods for Bayesian Filtering, par A Doucet, C Andrieu et S. Godsill, Statistics and Computing, vol. 10, no. 3, pp. 197-208, 2000 CiteSeer link
- Tutorial on Particle Filters for On-line Nonlinear/Non-Gaussian Bayesian Tracking (2001); S. Arulampalam, S. Maskell, N. Gordon et T. Clapp; CiteSeer link
- F. Dellaert, D. Fox, W. Burgard, et S. Thrun, "Monte Carlo Localization for Mobile Robots, " IEEE International Conference on Robotics and Automation (ICRA99), mai 1999.
- Inference in Hidden Markov Models, par O. Cappe, E. Moulines, T. Ryden. Publié par Springer.
Liens externes
- Méthodes de Monte-Carlo Séquentielles (Filtrage Particulaire) à l'Université de Cambridge
- Animations MCL de Dieter Fox
Catégories : Algorithme numérique | Filtre | Statistiques - La suite des paramètres
Wikimedia Foundation. 2010.

