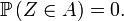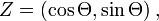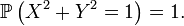- Theoreme de Radon-Nikodym-Lebesgue
-
Théorème de Radon-Nikodym-Lebesgue
Sommaire
Absolue continuité
Définition — Soit
 une mesure positive
une mesure positive  -finie sur
-finie sur 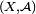 et soit
et soit 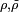 des mesures positives
des mesures positives  -finies (resp. réelles, resp. complexes) sur
-finies (resp. réelles, resp. complexes) sur 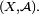
- On dit que
 est absolument continue par rapport à
est absolument continue par rapport à  si pour tout
si pour tout 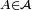 tel que
tel que 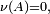 on a également
on a également 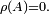 On note alors
On note alors
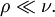
- On dit que
 est portée par
est portée par 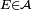 si pour tout
si pour tout 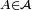 on a
on a
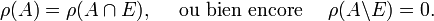
- On dit que
 et
et 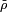 sont mutuellement étrangères s'il existe
sont mutuellement étrangères s'il existe 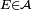 telle que
telle que  soit portée par
soit portée par 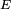 et
et 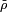 soit portée par
soit portée par 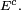 On note
On note
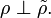
Théorème de Radon-Nikodym
En mathématiques, le théorème de Radon-Nikodym est un résultat de théorie de la mesure, cependant une preuve faisant intervenir les espaces de Hilbert a été donnée par le mathématicien John von Neumann au début du XXième siècle (voir par exemple le manuel Analyse réelle et complexe de Rudin pour de plus amples détails). Il s'énonce de la façon suivante :
Théorème de Radon-Nikodym — Soient
 une mesure positive
une mesure positive  -finie sur
-finie sur 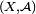 et
et  une mesure positive
une mesure positive  -finie (resp. réelle, resp. complexe) sur
-finie (resp. réelle, resp. complexe) sur 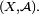 Alors :
Alors :(i) Il existe un unique couple de mesures
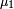 et
et 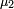 telles que :
telles que :- μ = μ1 + μ2
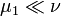
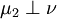
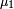 et
et 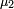 sont des mesures positives
sont des mesures positives  -finies (resp. réelles, resp. complexes).
-finies (resp. réelles, resp. complexes).(ii) Il existe une unique (à égalité
 -presque partout près) fonction
-presque partout près) fonction  mesurable positive (resp.
mesurable positive (resp.  -intégrable réelle, resp.
-intégrable réelle, resp.  -intégrable complexe), telle que pour tout
-intégrable complexe), telle que pour tout 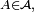 on ait
on ait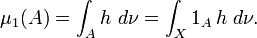
Densité d'une mesure
Définition — Soit
 une mesure positive
une mesure positive  -finie sur
-finie sur 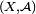 et soit
et soit  une mesure positive
une mesure positive  -finie (resp. réelle, resp. complexe) sur
-finie (resp. réelle, resp. complexe) sur 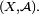 On dit que
On dit que  possède une densité
possède une densité  par rapport à
par rapport à  si
si  est une fonction mesurable positive (resp. ν-intégrable réelle, resp. ν-intégrable complexe), telle que pour tout
est une fonction mesurable positive (resp. ν-intégrable réelle, resp. ν-intégrable complexe), telle que pour tout 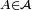 on ait
on ait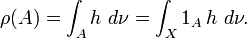
On note
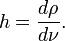
En conséquence du théorème de Radon-Nikodym, on a la propriété suivante :
Proposition — Soient
 une mesure positive
une mesure positive  -finie sur
-finie sur 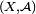 et
et  une mesure positive
une mesure positive  -finie (resp. réelle, resp. complexe) sur
-finie (resp. réelle, resp. complexe) sur 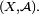 Alors on équivalence entre :
Alors on équivalence entre :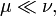
 possède une densité par rapport à
possède une densité par rapport à 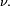
DémonstrationSi
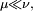 alors, clairement,
alors, clairement, 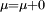 est un décomposition de
est un décomposition de  satisfaisant le Théorème de Radon-Nikodym, donc, en vertu de la dernière partie du Théorème,
satisfaisant le Théorème de Radon-Nikodym, donc, en vertu de la dernière partie du Théorème,  possède une densité par rapport à
possède une densité par rapport à 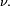 Réciproquement, notons
Réciproquement, notons  la densité de
la densité de  par rapport à
par rapport à 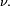 Si
Si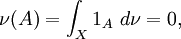
alors
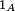 est nul
est nul  -presque partout. Il suit que
-presque partout. Il suit que 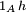 est nul
est nul  -presque partout également, donc
-presque partout également, donc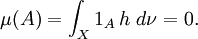
Densité de probabilité d'un vecteur aléatoire
Rappel —
- On appelle densité de probabilité d'une variable aléatoire
 à valeur dans
à valeur dans 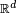 une fonction
une fonction 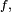 mesurable, telle que pour toute partie borélienne
mesurable, telle que pour toute partie borélienne 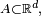
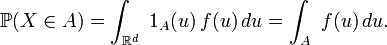
- La loi de probabilité
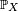 d'une variable aléatoire
d'une variable aléatoire  à valeur dans
à valeur dans 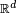 est la mesure de probabilité définie, pour toute partie borélienne
est la mesure de probabilité définie, pour toute partie borélienne 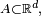 par
par
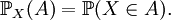
- Si
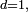
 est appelée une variable aléatoire réelle, ou encore v.a.r..
est appelée une variable aléatoire réelle, ou encore v.a.r..
Au vu des définitions, le langage probabiliste diffère légèrement du langage de la théorie de la mesure. Il y a équivalence entre les trois assertions :
- Une variable aléatoire
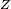 à valeur dans
à valeur dans 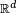 possède une densité de probabilité.
possède une densité de probabilité. - La mesure
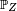 possède une densité par rapport à la mesure de Lebesgue sur
possède une densité par rapport à la mesure de Lebesgue sur 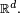
- La mesure
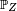 est absolument continue par rapport à la mesure de Lebesgue sur
est absolument continue par rapport à la mesure de Lebesgue sur 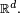
Le dernier point peut se réécrire, en langage probabiliste,
Critère — Une variable aléatoire
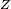 à valeur dans
à valeur dans 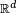 possède une densité de probabilité si et seulement si, pour chaque borélien
possède une densité de probabilité si et seulement si, pour chaque borélien 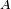 de
de 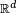 dont la mesure de Lebesgue est nulle, on a
dont la mesure de Lebesgue est nulle, on aCe critère est rarement employé dans la pratique pour démontrer que
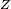 possède une densité, mais il est en revanche utile pour démontrer que certaines probabilités sont nulles. Par exemple, si le vecteur aléatoire
possède une densité, mais il est en revanche utile pour démontrer que certaines probabilités sont nulles. Par exemple, si le vecteur aléatoire 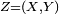 possède une densité, alors
possède une densité, alors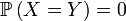 ,
,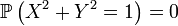 ,
,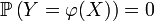 ,
,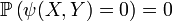 ,
,
pour des fonctions
 et
et 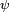 suffisamment régulières[1], parce que la mesure de Lebesgue (i.e. la surface) de la première bissectrice (resp. du cercle unité, du graphe d'une fonction, ou d'une courbe, suffisamment régulières) sont nulles.
suffisamment régulières[1], parce que la mesure de Lebesgue (i.e. la surface) de la première bissectrice (resp. du cercle unité, du graphe d'une fonction, ou d'une courbe, suffisamment régulières) sont nulles.Le critère de Radon-Nikodym peut aussi être utilisé pour démontrer qu'un vecteur aléatoire ne possède pas de densité : par exemple, si
où
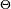 désigne une variable aléatoire suivant la loi uniforme sur
désigne une variable aléatoire suivant la loi uniforme sur ![\scriptstyle\ [0,2\pi],](/pictures/frwiki/98/b0ecfc21058ba22c4e187e60cb933f0b.png) alors
alors 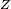 ne possède pas de densité car
ne possède pas de densité carRemarque — Dans le cas
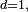 une variable aléatoire
une variable aléatoire 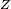 à valeur dans
à valeur dans 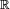 possède une densité de probabilité si et seulement si sa fonction de répartition est localement absolument continue.
possède une densité de probabilité si et seulement si sa fonction de répartition est localement absolument continue.Notes et références
- ↑ en effet il faut éviter des phénomènes de type "Courbe de Peano".
- Portail des mathématiques
Catégories : Théorème de mathématiques | Théorie de la mesure - On dit que
Wikimedia Foundation. 2010.