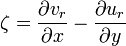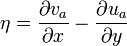Vorticité

Le tourbillon, parfois appelé vorticité (du latin vortex), est une formulation mathématique de la dynamique des fluides relié à la quantité de vitesse angulaire ou de rotation que subit un fluide localement. Une façon simple de visualiser le tourbillon est de considérer un fluide en mouvement dans lequel on délimite un petit volume rigide. Si cette parcelle tourne par rapport à un référentiel au lieu de translater, elle tourbillonne.

Sommaire 1 Terminologie 2 Dynamique des fluides 3 Météorologie et Océanographie 4 Autres utilisations 5 Bibliographie

Terminologie

La terminologie est assez fluctuante, pour une part à cause de la contamination par l'anglais.

Avant toute considération scientifique, un tourbillon est un mouvement de rotation d'une particule fluide tel que décrit dans le schéma voisin. En français technique le mot vortex représente généralement un tourbillon unique observé par exemple lors de la vidange d'une baignoire, à la différence de l'anglais pour lequel ce mot a un sens beaucoup plus général.

Comme toute rotation, le tourbillon est décrit comme un vecteur porté par l'axe de rotation dont l'intensité est égale à la vitesse de rotation. Il est commode de le caractériser par le vecteur tourbillon qui se calcule comme le rotationnel de la vitesse et a une intensité double de celle du vecteur rotation. Alors que le mot anglais vorticity représente généralement ce rotationnel, le mot français vorticité est plutôt associé à une zone tourbillonnaire (nappe de vorticité).

Dynamique des fluides

En dynamique des fluides, le tourbillon est le rotationnel de la vitesse du fluide. On peut également le considérer comme la circulation par unité de surface en un point dans un flux :

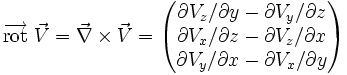
où 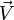est le vecteur tri-dimensionnel de vitesse selon les coordonnées x, y et z et l'opérateur nabla.

C'est une quantité vectorielle dont la direction est le long de l'axe de rotation du fluide. Ainsi, pour un flux à deux dimensions quelconque (a et b), le vecteur de tourbillon se retrouve dans l'axe perpendiculaire au plan de rotation (c) et l'équation se réduit à :

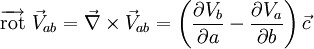
On retrouve différents théorèmes reliés au tourbillon en physique.

Météorologie et Océanographie

En météorologie et en océanographie physique, le tourbillon est une propriété importante du comportement à grande échelle de l'atmosphère et de l'océan. Les deux circulations, circulation atmosphérique et circulation océanique, étant surtout horizontales, le vecteur tourbillon pour ces deux milieux est généralement vertical. Donc si on reprend la formulation précédente, on obtient le tourbillon relatif en un point au-dessus de la Terre (V_r pour vitesse relative) :

Cette expression ne tient cependant pas compte du mouvement du référentiel qu'est la Terre. En effet, cette dernière est en rotation elle-même dans l'espace et nous devons ajouter la rotation induite par la force de Coriolis pour obtenir le tourbillon absolu (V_a pour vitesse absolue) :

En symbolisant par f le paramètre de Coriolis, nous obtenons : 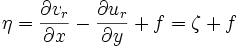, le paramètre de Coriolis étant donné par f = 2Ωsinφ où Ω est la rotation terrestre et φ la latitude.

Pour l'atmosphère et l'océan, les déplacements étant horizontaux, ce paramètre est souvent appelé tourbillon vertical planétaire, le tourbillon planétaire étant le double du vecteur rotation terrestre, soit 2Ω.

Dans l'hémisphère nord, le tourbillon est positif pour une rotation anti-horaire (cyclonique) et négative pour une rotation horaire (anti-cyclonique). C'est l'opposé dans l'hémisphère sud.

Le tourbillon en un point de l'atmosphère n'est pas conservatif en lui-même car l'épaisseur de la couche d'air peut être étirée ou compressée par le mouvement de l'air (ex. passage au-dessus d'une montagne). Cependant, le tourbillon total dans la colonne d'air est lui conservateur et on le nomme tourbillon potentiel. En effet, en général l'air subit une compression ou décompression adiabatique, l'entropie est conservée et le tourbillon total de la colonne ne changera pas. Le tourbillon potentiel devient donc une façon de suivre les mouvements verticaux dans une masse d'air avec température potentielle constante.

En météorologie, l'une des approximations est celle de l'atmosphère barotrope où il n'y a pas de variation de température dans une masse d'air. L'équation de tourbillon barotrope est donc une façon simple de prévoir le déplacement des creux et crêtes d'onde longue à une hauteur de 50 kPa. Dans les années 1950, le premier programme de prévision numérique du temps utilisa cette équation.

Autres utilisations

La notion de tourbillon est importante dans bien d'autres domaines de la dynamique des fluides. Par exemple, on peut estimer la distribution de la portance sur une aile d'avion d'envergure finie en supposant qu'à chaque section de l'aile est associé un tourbillon semi-infini vers l'aval. Il est alors possible de déterminer l'intensité de ces tourbillons en utilisant le critère selon lequel il n'y a pas de flux induit à travers la surface de l'aile. On additionne ensuite les intensités de tous les tourbillons pour trouver une valeur approchée de la circulation autour de l'aile. La portance est alors le produit de la circulation, de la vitesse de l'air et de sa masse volumique.

Bibliographie

• (en) Batchelor, G. K., (1967, reprinted 2000) An Introduction to Fluid Dynamics, Cambridge Univ. Press
• (en) Ohkitani, K., "Elementary Account Of Vorticity And Related Equations". Cambridge University Press. January 30, 2005. ISBN 0521819849
• (en) Chorin, Alexandre J., "Vorticity and Turbulence". Applied Mathematical Sciences, Vol 103, Springer-Verlag. March 1, 1994. ISBN 0387941975
• (en) Majda, Andrew J., Andrea L. Bertozzi, and D. G. Crighton, "Vorticity and Incompressible Flow". Cambridge University Press; 1st edition. December 15, 2001. ISBN 0521639484
• (en) Tritton, D. J., "Physical Fluid Dynamics". Van Nostrand Reinhold, New York. 1977. ISBN 0198544936
• (en) Arfken, G., "Mathematical Methods for Physicists", 3rd ed. Academic Press, Orlando, FL. 1985. ISBN 0120598205

Données et variables météorologiques
Données de mesure	Albédo • Foudre • Isotherme zéro degré (Niveau de congélation) • Nébulosité • Point de rosée • Point de givrage • Précipitation • Pression atmosphérique • Réflectivité radar (en dBZ) • Température • Température de surface de la mer • Température du thermomètre mouillé • Vent • Visibilité (Profondeur optique)
Variables	EIC • EPCD • Fréquence de Brunt-Väisälä • Gradient thermique adiabatique • Hélicité • Humidité relative • Humidité absolue • Humidité absolue de saturation • Instabilité latente • Instabilité potentielle • Longueur de Monin-Obukhov • Niveau de condensation par ascension • Niveau de convection libre • Rapport de mélange • Refroidissement éolien • Température équivalente • Température potentielle • Température pseudo-potentielle du thermomètre mouillé • Theta-e • Température virtuelle • Tourbillon
Concepts	Convection • Hygrométrie • Évapotranspiration
Indices	Indice WBGT • Indice humidex • Indice d'aridité • Refroidissement éolien • Indice forêt météo • Indice de rayonnement UV • Indice de soulèvement • Indice de stabilité de Showalter
Diagrammes	Diagramme climatique • Diagramme de Stüve • Émagramme • Hodographe • Skew-T • Téphigramme
Portail de la météorologie Glossaire de la météorologie

• Portail de la physique
• Portail de la météorologie