- Vecteur de Pointing
-
Vecteur de Poynting
Le vecteur de Poynting, noté Π, S, ou encore R est un vecteur dont la direction indique, dans un milieu isotrope, la direction de propagation d'une onde électromagnétique et dont l'intensité vaut la densité de puissance véhiculée par cette onde. Le module de ce vecteur est donc une puissance par unité de surface, c'est-à-dire un flux d'énergie.
Sommaire
Expression générale du vecteur de Poynting
Soient E et B le champ électrique et le champ magnétique. Alors, le vecteur de Poynting est défini par :
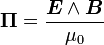 ,
,
où μ0 est la perméabilité du vide. Dans un matériau de perméabilité magnétique μ quelconque, il convient de prendre en compte l'excitation magnétique H définie par la relation B = μ H. L'expression plus générale du vecteur de Poynting est donc :
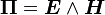 .
.
Moyenne temporelle en notation complexe
Dans le cas d'une onde électromagnétique plane progressive harmonique, on a
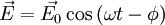 et
et  ; on peut donc associer des grandeurs complexes aux champs
; on peut donc associer des grandeurs complexes aux champs 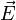 et
et 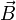 en posant
en posant 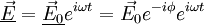 et
et 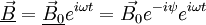 , où i est le nombre complexe tel que i2 = − 1.
, où i est le nombre complexe tel que i2 = − 1.La moyenne temporelle du vecteur de Poynting vaut alors
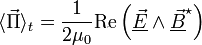 ,
,où
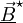 désigne le conjugué de
désigne le conjugué de 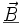 .
.Puissance électromagnétique traversant une surface Σ
Une conséquence du théorème de Poynting est que la puissance électromagnétique traversant une surface Σ est donnée par le flux du vecteur de Poynting à travers cette surface.
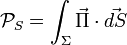
Équation de l'énergie d'un champ électromagnétique
Soit Uem énergie du champ électromagnétique :
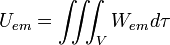 avec W densité volumique d'énergie (quantité d'énergie par unité de volume)
avec W densité volumique d'énergie (quantité d'énergie par unité de volume)On définit la quantité d'énergie quittant un volume τ pendant un temps δt :
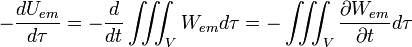
Soit
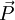 , vecteur flux d'énergie du champ. D'après le théorème de Green-Ostrogradsky (Théorème de flux-divergence) on peut dire que le flux sortant du volume V est :
, vecteur flux d'énergie du champ. D'après le théorème de Green-Ostrogradsky (Théorème de flux-divergence) on peut dire que le flux sortant du volume V est :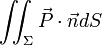 avec
avec 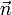 vecteur normal à la surface. Σ du volume, orienté vers l'extérieur
vecteur normal à la surface. Σ du volume, orienté vers l'extérieurOn peut expliciter la perte d'énergie du volume de la manière suivante :
- Pertes dues aux "frottements" des charges mobiles (voir Loi Ohm Locale, effet Joule).
- Pertes dues au rayonnement électromagnétique sortant du volume.
On peut donc dire que :
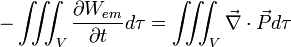 + travail fourni par le champ à la matière
+ travail fourni par le champ à la matièreCalculons ce travail :
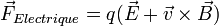
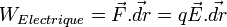 (on voit facilement que la force magnétique ne travaille pas.)
(on voit facilement que la force magnétique ne travaille pas.)Passons à la puissance fournie par le champ :
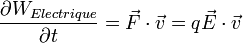 pour une charge.
pour une charge.On est dans le cas de N charges :
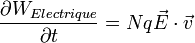 or
or 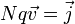
donc
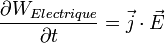
Cette perte de puissance est égale à la perte d'énergie du champ par unité de temps et de volume donc on écrit finalement :
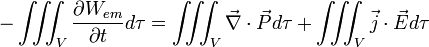
Donc finalement on a :
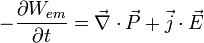 eq. de l'énergie du champ électromagnétique
eq. de l'énergie du champ électromagnétiqueVoir aussi
Liens internes
- Portail de la physique
- Portail de l’électricité et de l’électronique
Catégories : Électromagnétisme | Mécanique ondulatoire
Wikimedia Foundation. 2010.
