Vagues

Vagues

Vague

Page d'aide sur l'homonymie Pour les articles homonymes, voir vague (homonymie).
Une vague se brisant sur la côte sauvage de l'île d'Yeu

Une vague est une oscillation de la surface d'un océan, d'une mer ou d'un lac. Des oscillations de la pression et de la vitesse des fluides de part et d'autre de la surface sont associées aux vagues. Les vagues générées par le vent forment l'état de la mer et ont des amplitudes creux-à-crête allant de quelques centimètres à plus de 34 m, la plus haute vague jamais observée [1],[2]. Ces vagues sont irrégulières: des séries de vagues hautes (les groupes) sont suivies par des vagues plus petites.

Une mesure statistique de la hauteur des vagues est donnée par la hauteur significative. Des « vagues scélérates » plus hautes que deux fois la hauteur significative sont observées assez rarement, mais peuvent causer des dommages importants aux navires du fait de l'effet de surprise. Toutefois, ces vagues scélérates ne sont pas les plus hautes observées. En effet, une vague moyenne d'une très grosse tempête est plus haute qu'une vague scélérate d'un état de mer moyen. On peut bien sûr penser que la plus haute vague possible serait une vague scélérate dans une énorme tempête, mais il n'en existe pas d'observation.

Les séismes de forte puissance, éruptions volcaniques ou chutes de météorites créent également des vagues appelées tsunamis ou raz-de-marée, mais qui n'ont rien à voir avec la marée. La marée est à l'origine des mascarets qui se produisent lorsque l'onde de marée rencontre un courant opposé et de vitesse égale.

Sommaire

Diverses représentations mathématiques des vagues

Les vagues sont des ondes de gravité.

L'astronome et mathématicien George Biddell Airy a fourni la théorie la plus simple pour des vagues régulières (périodiques). L'onde d'Airy possède une surface libre de forme sinusoïdale. Il s'agit d'une représentation très simplifiée de la réalité, valable en principe pour des vagues régulières de faible cambrure. La cambrure est définie comme le rapport de la hauteur sur la longueur d'onde. Cette théorie est néanmoins efficace pour résoudre de nombreux problèmes pratiques, à condition de savoir associer des caractéristiques pertinentes au phénomène naturel beaucoup plus compliqué qui sera évoqué ci-dessous.

Si on regarde avec attention les vagues en mer, on constate que la plupart d'entre elles ne sont pas sinusoïdales: les crêtes sont plus pointues, les creux plus aplatis. Cet aspect est pris en compte en remplaçant l'approximation d'Airy, au premier ordre, par des approximations périodiques d'ordre supérieur généralement attribuées à Stokes.

Estampe japonaise, extraite des trente-six vues du Fuji de Katsushika Hokusai

En observant la succession des vagues, on s'aperçoit qu'elles ne présentent aucune régularité : il n'y a jamais deux vagues identiques. On est ainsi amené à décrire l'état de la mer de manière statistique. Un modèle simple repose sur l'analyse spectrale qui décompose la surface de la mer en une somme d'une infinité d'ondes infiniment petites ayant la même direction. Cette description basée sur une simple sommation de vagues d'Airy ne prend pas en compte les non-linéarités introduites par Stokes, imperfection dont on se satisfait très généralement.

Le modèle précédent, souvent suffisant pour décrire la houle observée loin de la zone de génération par le vent, doit être corrigé pour la mer du vent. Celle-ci superpose des ondes qui différent non seulement par leur longueur d'onde mais aussi par leur direction, ce qui donne à la mer son aspect désordonné (vagues à courtes crêtes). Faute de mieux on suppose, là aussi, que la superposition est conforme à la théorie linéaire.

Quand on veut, comme précédemment, utiliser une vague régulière pour simuler approximativement le phénomène naturel, on la caractérise généralement par sa hauteur significative, moyenne du tiers supérieur des hauteurs apparentes (crête-creux) qui est approximativement égale à quatre fois la moyenne quadratique des élévations, et par une période proche de celle qui contient le plus d'énergie.

Description des vagues régulières (périodiques) sur fond plat

Les vagues régulières sont despour lesquels une représentation mathématique du mouvement est assez simple.

Une vague périodique est caractérisée par

  • la profondeur d\,,
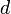  • la hauteur de crête à creux 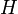H\, ou l'amplitude a\, qui est la moitié de celle-ci,
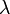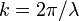  • et la longueur d'onde \lambda\, ou le nombre d'onde k = 2 \pi / \lambda\,.

En nombres sans dimension elle est caractérisée par

  • la cambrure a/\lambda\, ou le produit ka\,
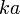
  • et la profondeur relative d/\lambda\, ou le produit kd\,.

La description des vagues relève du problème le plus simple de la mécanique des fluides qui ignore la viscosité, la compressibilité, l'existence de tourbillons (écoulement irrotationnel d'un fluide incompressible et parfait), la pente du fond, les irrégularités des vagues réelles et leur aspect tri-dimensionnel. Le caractère non-linéaire de la condition à la surface libre interdit néanmoins la recherche de solutions simples rencontrées dans d'autres problèmes physiques.

Vagues de Stokes

Une solution naturelle consiste à exprimer les différentes grandeurs par des développements limités en fonction du paramètre 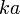ka\, supposé petit.

En supposant la vague infiniment petite le premier terme du développement fournit un modèle linéaire connu sous le nom de vague d'Airy. Celui-ci présente deux caractéristiques.

  • La surface libre est sinusoïdale.
  • En première approximation les trajectoires des particules fluides sont elliptiques. Toutefois, le calcul exact des trajectoires, même pour une vague linéaire, fait ressortir une dérive qui s'atténue de la surface vers le fond: c'est la dérive de Stokes. Pour les vagues linéaires, le débit associé à la propagation de la vague est égal à E / C,, avec E la densité d'énergie par unité de surface et C la vitesse de phase.

Pour les vagues réelles d'amplitude finie, cette description est assez sommaire, en particulier pour des profondeurs faibles par rapport à la longueur d'onde. Elle est néanmoins fréquemment utilisée à cause de sa simplicité. Des modèles non-linéaires d'ordres supérieurs peuvent être obtenus en ajoutant des corrections proportionnelles à des puissances de 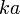ka\,. Ils améliorent en général le réalisme du modèle linéaire en ce qui concerne les deux points précédents.

  • À mesure que les ordres d'approximation s'élèvent la surface libre présente de crêtes de plus en plus pointues et des creux de plus en plus aplatis. L'approximation du cinquième ordre est généralement jugée assez réaliste pour leur description, sauf en eau peu profonde. Dans tous les cas on peut calculer exactement la solution numérique.
mouvement et dérive des particules en faible profondeur
  • Dès le deuxième ordre, les trajectoires s'ouvrent pour ressembler vaguement à des cycloïdes allongées. Ce phénomène traduit une dérive ou transport de masse qui correspond à la moyenne des vitesses horizontales.

Vagues en eau peu profonde

Le développement limité de Stokes perd de sa signification lorsque la profondeur relative devient inférieure à 1/8 environ. Dans ces conditions on observe des crêtes très pointues séparées par des creux très étendus. Ce phénomène est pris en compte par le modèle de la vague cnoïdale qui tend vers deux limites :

  • La vague sinusoïdale lorsque la hauteur est petite par rapport à la profondeur.
  • L'onde solitaire lorsque la longueur d'onde est grande par rapport à la profondeur. L'onde qui se situe alors entièrement au-dessus du niveau de repos ne présente plus de périodicité.


Instabilité des vagues périodiques

En pratique les vagues ne sont jamais exactement périodique, même en laboratoire, car les solutions mathématiques périodiques sont instable: les vagues évoluent vers d'autres formes, avec des trains de vagues irréguliers (instabilité modulationnelle de Bejamin et Feir) ou vers le déferlement (instabilité de la crête, mise en évidence par Tanaka). De nombreuses autres instabilités existent qui peuvent créer spontanément des formes en trois dimensions (vagues en fer à cheval par exemple).

Propagation des vagues (Modèle d'Airy)

Un modèle simple établi par Airy permet d'obtenir quelques caractéristiques des vagues.

Onde d'Airy de période 2 secondes par 3 mètres de fond. À gauche: vitesses et variations de pression, à droite trajectoire de particules suivies pendant 4 secondes.

Relation de dispersion

Le mouvement des vagues peut être considéré comme irrotationnel, il dérive donc d'un potentiel. Comme l'eau est pratiquement incompressible, ce potentiel satisfait l'équation de Laplace. Les solutions périodiques de faible amplitude obéissent à une relation de dispersion

{\omega}^2 =g k \cdot \tanh (k H)

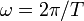avec \omega = 2 \pi / T\, la pulsation de l'onde, 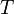T\, la période de la houle, 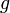g\, l'intensité de la pesanteur, 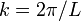k= 2 \pi / L\, le nombre d'onde, 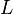L\, la longueur d'onde de la houle et 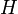H\, la profondeur de l'eau. Cette relation permet d'aboutir à une expression simplifiée de la célérité de propagation de l'onde :

c=\frac{{\omega}}{k} = \sqrt{\frac{g}{k}\tanh(kH)}

Comme on a brutalement simplifié les équations de départ pour établir cette relation, elle n'est valable que pour des vagues de faible amplitude par rapport à la profondeur de l'eau et de cambrure ka faible (ou a est l'amplitude des vagues). Ce dernier critère correspond à des vagues pas trop "pentues".

On peut néanmoins tirer de cette relation quelques propriétés intéressantes : notamment, à profondeur importante, la vitesse des vagues ne dépend plus de la profondeur puisque la tangente hyperbolique tend vers 1. De façon plus qualitative, on peut comprendre le comportement des vagues à l'approche du littoral. Quand la profondeur diminue, la pulsation (ou la période) reste constante. Les formules ci-dessus entraînent l'augmentation du nombre d'onde, donc la diminution de la longueur d'onde et de la célérité. La vitesse de groupe 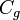C_g\,, vitesse du transport d'énergie décroît elle aussi. Pour que l' énergie du système soit conservée alors qu'elle est transportée à une vitesse plus faible il faut que la densité d'énergie par mètre carré augmente. Or cette densité d'énergie, est, en joules par mètres carrés, égale à \rho g a^2\, . 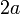La hauteur des vagues 2a\, doit donc augmenter et elles finissent par déferler, lorsque la vitesse des particules d'eau atteint la vitesse de phase de la vague qui les supporte<

Pour simplifier en se limitant au cas de la profondeur infinie :

  • Célérité (vitesse de propagation ou vitesse de phase) en m/s : C= 1.25\sqrt{L}
  • Période (temps qui sépare deux crêtes) : T= 0.8\sqrt{L}
  • Longueur d'onde: L=1,6T^2\,

Réflexion, diffraction et réfraction

Une vague formée par un ferry

Comme toutes les ondes, en particulier les ondes lumineuses, les vagues peuvent se réfléchir, se diffracter et se réfracter.

La réflexion se produit sur un ouvrage de hauteur immergée importante par rapport à la profondeur et de largeur importante par rapport à la longueur d'onde. Elle est totale sur une digue verticale, partielle sur une digue à talus. Une forte réflexion est aussi possible au-dessus d'un relief sous-marin présentant une série de bosses espacées de la moitié de la longueur d'onde [3].

Les phénomènes se compliquent au voisinage d'un obstacle de dimensions relativement petites vis-à-vis des longueurs d'onde, comme un navire, ou de l'extrémité d'une jetée. La réflexion, notion d'optique géométrique, n'est plus applicable car les vagues contournent l'obstacle et produisent ainsi une agitation dans l'ombre. Il faut alors faire appel à la notion de diffraction.

La diminution de c avec la profondeur conduit aussi à des phénomènes de réfraction, exactement analogues à ceux observés en optique. De même que les surfaces d'onde suivent les lignes iso-indice, les vagues tendent à épouser la forme des lignes d'égale vitesse (c’est-à-dire les isobathes ou lignes d'égale profondeur) et à ainsi à épouser le littoral. Les vagues se concentrent donc autour des pointes, où leur hauteur est plus grande, et s'évasent dans les baies. Les courants modifient aussi la vitesse de phase et la relation de dispersion. Ils induisent donc aussi une réfraction.

Mouvement du fluide

Dans la théorie d'Airy, les particules de fluide décrivent des ellipses fixes, dont la taille décroît avec la profondeur. En eau profonde (profondeur supérieure à la moitié de la longueur d'onde) ces ellipses sont des cercles.

Les théories d'ordre supérieur prévoient un faible mouvement global du fluide : la dérive de Stokes. Près de la surface libre, la vitesse d'une particule d'eau est plus importante sous une crête que la vitesse opposée lors du passage du creux suivant. Il en résulte une dérive dans le sens de propagation des vagues qui peut s'inverser en profondeur. Pour les vagues générées par le vent, cette dérive est d'environ 1,5 % de la vitesse du vent pour un état de mer complètement développé et en eau profonde.

Validité et limitations

La première limitation réside dans l'irrégularité des vagues en mer.

Pour une vague isolée l'approximation d'Airy est particulièrement bien vérifiée dans le cas de la houle constituée par des vagues peu cambrées se propageant au large et soumises à peu de vent. À mesure que la cambrure augmente, elle devient de plus en plus imprécise mais est néanmoins souvent utilisée à cause de sa simplicité. Dans certains problèmes exceptionnels, le niveau maximum atteint par une vague peut devenir critique et une approximation supérieure est utilisée, généralement celle de Stokes cinquième ordre.

Cette approximation devient très imparfaite dans les faibles profondeurs et doit être remplacée par exemple par l'approximation cnoïdale.

Elle est également imparfaite dans une zone de déferlements, que ce soit dans la zone de génération de la mer du vent ou sur des hauts fonds.

Déferlement

Description

Au large, la houle observée en l'absence de vent donne une impression de régularité, ce qui ne correspond pas tout à fait à la réalité. En fait, elle est constituée d'ondes de différentes célérités. Le rattrapage de ces ondes conduit de temps en temps à des vagues trop cambrées pour se maintenir : elles déferlent. Dans la mer du vent, les vagues poussées par le vent déferlent également sous l'action de celui-ci.

À l'approche d'un rivage, à mesure que la profondeur diminue, la forme des vagues se modifie, d'abord à peu près symétriquement puis en général avec une face avant de plus en plus raide jusqu'à l'instabilité qui se produit lorsque la hauteur de la vague est du même ordre que la profondeur. Quand la vague se brise, une partie de son énergie est dissipée en tourbillons, turbulence et frottement sur le fond. Une autre partie engendre des ondes réfléchies et des courants qui jouent un rôle essentiel dans les mouvements de sable sur les plages.

La forme d'un déferlement au voisinage du rivage dépend essentiellement de la pente des fonds. En allant dans le sens des pentes croissantes on distingue le plus souvent trois types de déferlement. Le déferlement progressif ou glissant (spilling breaker en anglais) se produit généralement sur les plages à très faible pente. Les vagues commencent à se briser loin du rivage avec une crête à l'aspect mousseux qui s'accentue lors de la progression en laissant derrière une couche d'écume.

Le déferlement plongeant (plunging breaker en anglais) est particulièrement spectaculaire avec ses rouleaux appréciés par les surfers. La vague s'enroule autour d'une poche d'air puis s'écroule en créant une éclaboussure notable. Cela tend à se produire le plus souvent sur une forte pente ou sur un changement brutal de la profondeur (un rebord rocheux ou un écueil). Il y a beaucoup plus d'énergie dissipée que d'énergie réfléchie sur la plage.

Le déferlement frontal ou gonflant (surging breaker en anglais) se forme comme le déferlement plongeant mais la vague gravit la plage avant que la crête puisse s'enrouler. La zone de déferlement est très étroite et une grande partie de l'énergie est réfléchie vers les plus grandes profondeurs.

Certains considèrent aussi un cas intermédiaire entre les déferlements plongeant et gonflant (collapsing breaker). Au lieu de constituer un rouleau, la vague présente une face verticale avant de s'effondrer.

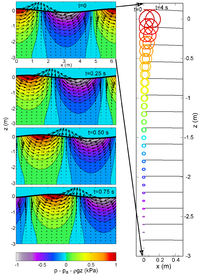
Simulation numérique

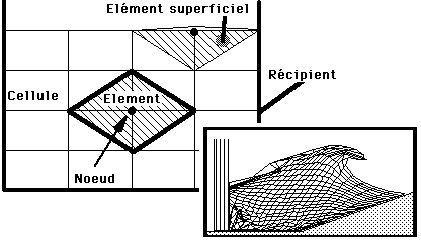Vague solitaire déferlante calculée par différences finies

Le mouvement d'une vague créée dans un canal à houle par un générateur de vagues du type piston a été simulé sur microordinateur par un calcul de différences finies[4].

La méthode de calcul consiste à découper le volume fluide en quadrilatères où la pression et les autres paramètres sont constants et à diviser le temps en petits intervalles égaux. On associe à chaque nœud du maillage ainsi créé un élément obtenu en joignant entre eux les quatre nœuds voisins. On applique pour chaque pas de temps à cet élément les lois fondamentales de la mécanique qu'on intègre par différences finies au premier ordre. Le fluide est homogène, pesant et compressible. Le logiciel a été validé par comparaison avec des résultats expérimentaux et numériques issus de la littérature, concernant des vagues de moyenne amplitude. En faisant varier la profondeur et la vitesse du piston on a trouvé que la vitesse de la base de la vague ne dépend que de la profondeur mais que la vitesse de la crête est double de celle du piston.

Photos

Tempête à Pors-Loubous.jpg
Port de Bestrée.jpg

Voir également

Liens externes

Notes et références

  1. ↑ Observation visuelle: Ocean Waves, Bascom, W., 1959: Scientific American.
  2. ↑ Enregistrement d'un instrument en mer, la vague la plus haute mesurait 32,3 m Monstrous ocean waves during typhoon Krosa, P. C. Liu, H. S. Chen, D.-J. Doong, C. C. Kao, and Y.-J. G. Hsu, 2008: Annales Geophysicae, vol. 26, pp. 1327-1329.
  3. ↑ Seabed-wave resonance and sand bar growth, Heathershaw, A. D., 1982: Nature, 296, 343-345.
  4. ↑ Schaeffer, B., Possibilités des microordinateurs - Simulation numérique d'une vague déferlante, dont le mouvement en profondeur et le profil sont calculés par microordinateur. Association Technique Maritime et Aéronautique, session 1988, Paris ATMA 88.[1]
  • Portail du monde maritime Portail du monde maritime
Ce document provient de « Vague ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Vagues de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Vagues invisibles — (Invisible waves) est un film thaïlandais et néerlandais, réalisé par Pen ek Ratanaruang, sorti en 2006. Sommaire 1 Synopsis 2 Fiche technique 3 Distribution 4 …   Wikipédia en Français

  • Vagues scélérates — Vague scélérate Vague scélérate vue d’un navire marchand (1993). Les vagues scélérates sont des vagues océaniques très hautes, soudaines et qui étaient considérées comme très rares, même si aujourd’hui on sait qu’elles apparaissent pratiquement… …   Wikipédia en Français

  • Vagués (Buenos Aires) — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Theorie des vagues d’Elliott — Théorie des vagues d’Elliott Sommaire 1 La théorie 2 Notes et références 3 Les règles 3.1 La personnalité des vagues …   Wikipédia en Français

  • Théorie des vagues d'Elliott — Théorie des vagues d’Elliott Sommaire 1 La théorie 2 Notes et références 3 Les règles 3.1 La personnalité des vagues …   Wikipédia en Français

  • Théorie des vagues d’Elliott — Sommaire 1 La théorie 2 Les règles 2.1 La personnalité des vagues 2.1.1 La vague 1 2.1.2 La va …   Wikipédia en Français

  • Théorie des vagues d’elliott — Sommaire 1 La théorie 2 Notes et références 3 Les règles 3.1 La personnalité des vagues …   Wikipédia en Français

  • Theorie des vagues de developpement — Théorie des vagues de développement Dans une série d’ouvrages publiés entre 1971 et 1994, dont les plus marquants sont Le Choc du futur, La Troisième vague et Les Nouveaux pouvoirs, Alvin Toffler et son épouse Heidi ont développé une idée fondée… …   Wikipédia en Français

  • Trois vagues de développement de l'humanité selon Alvin et Heidi Toffler — Théorie des vagues de développement Dans une série d’ouvrages publiés entre 1971 et 1994, dont les plus marquants sont Le Choc du futur, La Troisième vague et Les Nouveaux pouvoirs, Alvin Toffler et son épouse Heidi ont développé une idée fondée… …   Wikipédia en Français

  • Trois vagues de développement de l’humanité selon Alvin et Heidi Toffler — Théorie des vagues de développement Dans une série d’ouvrages publiés entre 1971 et 1994, dont les plus marquants sont Le Choc du futur, La Troisième vague et Les Nouveaux pouvoirs, Alvin Toffler et son épouse Heidi ont développé une idée fondée… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”