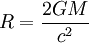Gravite de surface

Gravite de surface

Gravité de surface

En astronomie, la gravité de surface est l'intensité du champ gravitationnel à la surface d'un objet astrophysique (planète, étoile ou autre). Ce concept est également utilisé, quoique de façon légèrement différente, dans la physique des trous noirs où il règle la vitesse à laquelle le champ gravitationnel au sens classique du terme diverge à l'approche de la surface du trou noir, c'est-à-dire de son horizon.

En physique stellaire, la coutume est d'utiliser le logarithme décimal de la valeur exprimée dans le système CGS (cm/s²).

Sommaire

Formule newtonnienne

Dans le cadre de la mécanique newtonienne, la gravité de surface est donnée par la formule habituelle du champ gravitationnel d'un objet sphérique, à savoir

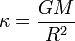\kappa = \frac{G M}{R^2},

où G est la constante de gravitation, M la masse de l'objet considéré et R son rayon, l'objet étant considéré à peu près sphérique.

Cas des trous noirs

Dans le cadre de la physique des trous noirs, il est possible de définir un analogue du concept de gravité de surface. Il faut cependant prendre garde au fait qu'un trou noir peut être presque par définition considéré comme un objet à la « surface » duquel (c'est-à-dire au niveau de son horizon) le champ gravitationnel est infini. Il existe cependant une autre quantité qui diverge à mesure que l'on s'approche de l'horizon d'un trou noir : il s'agit du décalage vers le rouge d'origine gravitationnelle que subissent les signaux émis depuis cette zone. Dans ce cadre-là, on définit la gravité de surface d'un trou noir par la limite du rapport entre l'intensité du champ gravitationnel au décalage vers le rouge causé par le trou noir. On peut alors montrer que cette quantité reste finie quand on approche l'horizon, et que dans le cas le plus simple d'un trou noir de Schwarzschild, sa valeur est égale à celle que l'on déduirait naïvement dans un traitement newtonien, c'est-à-dire qu'elle vaut à nouveau G M / R2.

Formule et cas particuliers

L'expression exacte de la gravité de surface s'écrit, en unités géométriques,

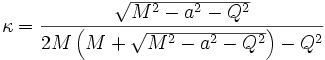\kappa = \frac{\sqrt{M^2 - a^2 - Q^2}}{2 M \left(M + \sqrt{M^2 - a^2 - Q^2} \right) - Q^2},

où M, Q, a représentent respectivement la masse, la charge électrique et le moment cinétique réduit (c'est-à-dire le rapport du moment cinétique à la masse) du trou noir.

Dans le cas d'un trou noir de Schwarzschild, c'est-à-dire ne possédant ni charge électrique ni moment cinétique, on obtient

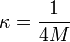\kappa = \frac{1}{4 M},

ce qui donne, avec les unités du système international,

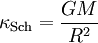\kappa_{\rm Sch} = \frac{G M}{R^2},

avec

R = \frac{2 G M}{c^2}

correspondant au rayon de Schwarzschild.

Pour un trou noir extrémal, pour lequel la quantité M2 − Q2 − a2 s'annule, on a

κExt = 0.

Propriétés de la gravité de surface d'un trou noir

La principale propriété de la gravité de surface d'un trou noir est qu'elle est strictement constante sur toute la surface du trou noir. Ce résultat est logique dans le cas d'un trou noir à symétrie sphérique (trou noir de Schwarzschild et de Reissner-Nordström), mais il est plus surprenant quand le trou noir est non sphérique du fait de sa rotation (trou noir de Kerr ou de Kerr-Newman).

La gravité de surface peut être déterminée en calculant la dérivée partielle de la masse d'un trou noir quelconque par rapport à sa surface A en gardant fixés sa charge électrique Q et son moment cinétique L, selon la formule

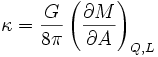\kappa = \frac{G}{8 \pi} \left(\frac{\partial M}{\partial A}\right)_{Q, L}.

De ce fait, la différentielle de la masse d'un trou noir s'écrit dans le système d'unités géométriques,

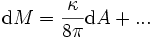{\rm d} M = \frac{\kappa}{8 \pi} {\rm d} A + ....

Le fait que la surface d'un trou noir croisse nécessairement au cours du temps, et que la gravité de surface soit contante sur l'horizon d'un trou noir est à rapprocher des principes de la thermodynamique qui disent que la température d'un objet à l'équilibre est partout la même dans l'objet et que son entropie ne peut que croître avec le temps. Ce fait n'est en réalité pas anodin et est à l'origine du développement d'une analogie profonde entre trous noirs et thermodynamique : la thermodynamique des trous noirs. La démonstration de ce résultat est relativement complexe, et est due à Brandon Carter, Stephen Hawking et James Bardeen, en 1973[1].

Notes

  1. ↑ (en) James M. Bardeen, Brandon Carter & Stephen Hawking, The Four laws of Black Hole Mechanics, Communications in Mathematical Physics, 31, 161-170 (1973) Voir en ligne.

Références

  • Portail de l’astronomie Portail de l’astronomie
Ce document provient de « Gravit%C3%A9 de surface ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Gravite de surface de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Gravité De Surface — En astronomie, la gravité de surface est l intensité du champ gravitationnel à la surface d un objet astrophysique (planète, étoile ou autre). Ce concept est également utilisé, quoique de façon légèrement différente, dans la physique des trous… …   Wikipédia en Français

  • Gravité de surface — En astronomie, la gravité de surface est l intensité du champ gravitationnel à la surface d un objet astrophysique (planète, étoile ou autre). Ce concept est également utilisé, quoique de façon légèrement différente, dans la physique des trous… …   Wikipédia en Français

  • Gravité — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le mot gravité (du latin gravitas, pesanteur) peut avoir plusieurs sens : Dans les sciences physiques, la gravité est la force d attraction exercée… …   Wikipédia en Français

  • Gravite artificielle — Gravité artificielle La gravité artificielle est une simulation de la gravité dans l espace ou en chute libre. Ceci faciliterait les voyages dans l espace en évitant les problèmes liés à l impesanteur. Sommaire 1 Créer une gravité artificielle… …   Wikipédia en Français

  • Gravité Artificielle — La gravité artificielle est une simulation de la gravité dans l espace ou en chute libre. Ceci faciliterait les voyages dans l espace en évitant les problèmes liés à l impesanteur. Sommaire 1 Créer une gravité artificielle 1.1 Rotation 1.2… …   Wikipédia en Français

  • SURFACE (PHÉNOMÈNES DE) — La surface d’un solide ou d’un liquide est une région s’étendant sur quelques distances atomiques qui sépare l’intérieur du matériau du milieu extérieur: en général, le vide ou un gaz. Si le milieu extérieur est une autre phase dense, liquide ou… …   Encyclopédie Universelle

  • Surface de sustentation — Pour les articles homonymes, voir Surface (homonymie). En mécanique du solide, on appelle surface de sustentation la surface sur laquelle la projection orthogonale du centre de gravité d un solide sur le sol, ou sur un support, doit se trouver… …   Wikipédia en Français

  • Gravité artificielle — La gravité artificielle est une simulation de la gravité dans l espace ou en chute libre. Ceci faciliterait les voyages dans l espace en évitant les problèmes liés à l impesanteur. Sommaire 1 Créer une gravité artificielle 1.1 Rotation 1.2… …   Wikipédia en Français

  • Surface — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le mot « surface », du latin superficies désigne la partie apparente d un corps, puis une couche peu profonde[1]. Il est parfois utilisé pour… …   Wikipédia en Français

  • Gravité spécifique — Densité Pour les articles homonymes, voir Densité (homonymie). La densité ou densité relative d un corps est le rapport de sa masse volumique à la masse volumique d un corps pris comme référence. Le corps de référence est l eau pure à 4 °C… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”