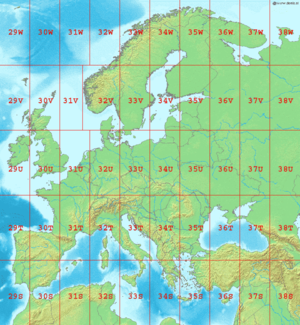
Transverse Unverselle de Mercator

Transverse Unverselle de Mercator: Transverse Universelle de Mercator

La Transverse universelle de Mercator (en anglais Universal Transverse Mercator ou UTM) est un type de projection conforme de la surface de la Terre. L’Allemagne l’utilise sous le nom de Projection de Gauss-Krüger. Cette projection est une projection cylindrique où l’axe du cylindre croise perpendiculairement l’axe des pôles de l’ellipsoïde terrestre au centre de l’ellipsoïde.

Schéma de la projection UTM

L'UTM est également un système de référence géospatiale permettant d'identifier n'importe quel point sur notre planète.

En pratique, pour couvrir la surface de la Terre, on la découpe en 60 fuseaux de 6 degrés en séparant l’hémisphère Nord et l’hémisphère Sud. Soit au total 120 zones (60 pour le Nord et 60 pour le Sud). On développe alors le cylindre tangent à l’ellipsoïde le long d’un méridien pour obtenir une représentation plane.

Les zones polaires (au-delà de 84,5 degrés de latitude Nord et en deçà de 80,5 degrés de latitude Sud) ne sont théoriquement pas couvertes par ce système de projection, bien que le cylindre utilisé soit tangent aux deux pôles.

Ce n’est cependant pas un réel obstacle, si on admet d’étendre le découpage rectangulaire de la projection, de façon à couvrir plus de 6° de longitudes au-delà de l’équateur. C’est ce qui est généralement utilisé sur les cartes, où l’extension de longitude permet de conserver une bonne précision à peu près similaire à celle du long de l’équateur.

Une variante plus exacte de cette projection est de ne pas utiliser un cylindre parfait, mais un cylindroïde aplati aux pôles et tangent tout le long des deux méridiens opposés au géoïde (ellipsoïdal) de référence.

L’intérêt de cette variante est de conserver les distances tout le long du méridien de référence. Dans ce cas aussi, la précision des distances autour des pôles ne dépend plus du méridien de référence choisi pour la projection, il devient alors possible de construire une carte rectangulaire continue couvrant la totalité des deux fuseaux opposés le long d’une fine bande (large de 6° exactement à l’équateur).

Le territoire français est situé sur 3 fuseaux :

UTM Nord, fuseau 30 : entre 6 degrés ouest et 0 degré Greenwich ;

UTM Nord, fuseau 31 : entre 0 degré et 6 degrés est Greenwich ;

UTM Nord, fuseau 32 : entre 6 degrés est et 12 degrés est Greenwich.

Une projection ne doit pas être confondue avec un système géodésique (par exemple WGS72, WGS84, RGF93) permettant de localiser un point à la surface de la Terre. N'importe quelle projection peut être associée à n'importe quel système géodésique; si aujourd'hui le système géodésique utilisé est généralement basé sur WGS84, il convient toutefois, pour éviter les ambiguïtés, d'associer les noms du système géodésique et de la projection ; par exemple en France le système géodésique NTF est resté jusqu'à récemment le système réglementaire et est généralement associé à la projection Lambert II étendu, mais on trouve aussi les projections Lambert Zone I à IV.

La projection UTM est associée à un point de référence virtuel situé :

Pour l’hémisphère Nord : sur l’équateur à 500 km à l’Ouest du méridien central de la zone considérée ;

Pour l’hémisphère Sud : sur le parallèle situé à 10 000 km au Sud de l’équateur et 500 km à l’Ouest du méridien central de la zone considérée.

Ce décalage de point de référence permet d’avoir des coordonnées positives pour l’intégralité des points de la zone.

Sommaire

1 Coordonnées : géographiques ou projection ?

2 Formules de passage de latitude,longitude (φ,λ) aux coordonnées UTM (E,N)

2.1 Les formules avec une précision du centimètre

2.2 Démonstration des formules

2.2.1 Etape 1: les coordonnées de Mercator généralisées (x,y)

2.2.2 Etape 2: des coordonnées de Mercator généralisées (x,y) vers les coordonnées UTM (E,N)

2.2.3 Etape 3: Des coordonnées de Mercator généralisé aux coordonnées Lambert

3 Voir aussi

4 Références

Coordonnées : géographiques ou projection ?

L’utilisation des coordonnées en projection (ex : E et N UTM) plutôt que des coordonnées géographiques (Latitude /Longitude) est en général jugée avantageuse pour les raisons suivantes :

Les coordonnées sont basées sur un système décimal, plus facile à utiliser pour les calculs que le système sexagésimal. Cependant avec des longitudes et latitudes on peut toujours travailler en degrés "décimaux" sans avoir à utiliser des minutes et des secondes d’angles ;

Le système est "rectangulaire" et est mesuré en kilomètres. On peut donc directement calculer des distances approximatives à partir des coordonnées UTM. Un point de la zone UTM 13 qui a pour coordonnées (315,1 km, 3 925,1 km) est exactement à 1 kilomètre du point de la zone 13 (315,1 km, 3 924,1 km). Cependant cette correspondance n’est qu’approchée si les points ne sont pas sur le même méridien, et elle n’est plus du tout valable lorsque l’on change de zone.

Les récepteurs GPS fournissent de manière standard une position dans le système géodésique WGS84. La plupart des cartes de randonnées récentes utilisent la projection UTM et se réfèrent au système géodésique WGS84. D’autres cartes utilisent une projection nationale ou locale, se référant à d'autres système géodésique (par exemple en France, les cartes de randonnée de l'IGN utilisaient une projection Lambert, et ont indiqué les coordonnées UTM sur les marges extérieures).

Formules de passage de latitude,longitude (φ,λ) aux coordonnées UTM (E,N)

Les formules avec une précision du centimètre

Les formules exactes sont compliquées et peu utilisables. Nous proposons des formules approchées avec une précision de l'ordre du centimètre.

Par convention, le géoïde WGS 84 décrit la terre par un ellipsoïde de révolution d'axe Nord-Sud, de rayon à l'équateur a=6378,137 km et d'excentricité e=0,0818192. On considère un point de latitude géodésique φ et longitude λ. Notons $λ 0$ la longitude du méridien de référence.

Les angles sont exprimés en radian. Voici des valeurs intermédiaires à calculer:

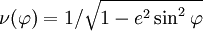
$\nu(\varphi)=1/\sqrt{1-e^{2}\sin^{2}\varphi}$

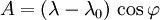
$A=(\lambda-\lambda_{0})\,\cos\varphi$

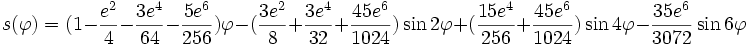
$s(\varphi) = (1-\frac{e^{2}}{4}-\frac{3e^{4}}{64}-\frac{5e^{6}}{256})\varphi-(\frac{3e^{2}}{8}+\frac{3e^{4}}{32}+ \frac{45e^{6}}{1024})\sin2\varphi + (\frac{15e^{4}}{256}+\frac{45e^{6}}{1024})\sin4\varphi-\frac{35e^{6}}{3072}\sin6\varphi$

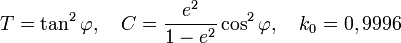
$T=\tan^{2}\varphi, \quad C=\frac{e^{2}}{1-e^{2}}\cos^{2}\varphi, \quad k_{0}=0,9996$

Dans l'hémisphère Nord $N 0 = 0$ et dans l'hémisphère Sud $N 0 = 10000 k m$ .

Voici les formules de passage donnant les coordonnées UTM $E, N$ en kilomètres:

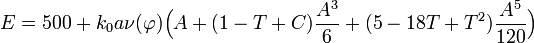
$E = 500 +k_{0}a\nu(\varphi)\Big(A+(1-T+C)\frac{A^{3}}{6}+(5-18T+T^{2})\frac{A^{5}}{120}\Big)$

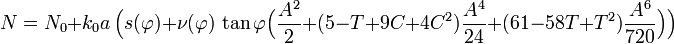$N =N_{0}+k_{0}a\,\Big(s(\varphi)+ \nu(\varphi)\,\tan\varphi\Big(\frac{A^{2}}{2}+(5-T+9C+4C^{2})\frac{A^{4}}{24} +(61-58T+T^{2})\frac{A^{6}}{720}\Big)\Big)$

Un exemple détaillé d'utilisation des formules

Prenons $λ =$ 5°50'51", 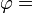$\varphi=$ 45°09'33", on est dans le fuseau 31, $λ 0 =$ 3°. Vous devez trouvez:

$λ - λ 0 = 0.0496983$ radians

$A = 0.0350442107$ ,

$C = 0.0033510263$ ,

$T = 1.01117395$ ,

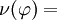$\nu(\varphi)=$ 1.00169,

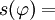$s(\varphi)=$ 0.784340804,

et enfin

$E = 723.80393$ et $N = 5004.57704$

Démonstration des formules

Faisons une remarque préalable: le terme de "projection de Mercator" pourrait laisser entendre qu'il y a une droite joignant un point du géoïde au point correspondant du cylindre qui l'enroule. Ce n'est pas le cas. Ce n'est pas le cas non plus pour la plupart des projections cartographiques comme la "projection de Lambert" entre le géoïde et un cône tangent. C'est le cas cependant pour la projection stéréographique. Par conséquent nous n'allons pas démontrer les formules à l'aide d'une projection.

Nous allons démontrer les formules en deux étapes. La première étape généralise l'emploi des coordonnées conformes de Mercator de la sphère au cas d'un ellipsoïde de révolution. Nous les appellerons coordonnées de Mercator généralisées.

La deuxième étape est une transformation conforme des coordonnées de Mercator généralisées vers les coordonnées UTM, avec la convention que ces coordonnées coïncident le long du méridien de référence.

Une troisième étape reprend la même démarche pour retrouver de façon directe les coordonnées de Lambert.

Etape 1: les coordonnées de Mercator généralisées (x,y)

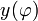Comme pour la projection de Mercator nous posons $x = λ$ . Cela va déterminer la fonction $y(\varphi)$ .

Appelons 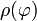$\rho(\varphi)$ la distance entre le point considéré de l'ellipsoïde et l'axe nord-sud. Appelons 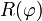$R(\varphi)$ le rayon de courbure le long du méridien. Un petit déplacement 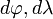$d\varphi,d\lambda$ sur l'ellipsoïde correspond à une distance: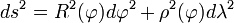

$ds^{2}=R^{2}(\varphi)d\varphi^{2}+\rho^{2}(\varphi)d\lambda^{2}$

appelée tenseur métrique de l'ellipsoïde.

L'exigence que $x, y$ soient des coordonnées conformes impose au tenseur métrique de s'écrire:

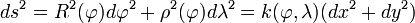
$ds^{2}=R^{2}(\varphi)d\varphi^{2}+\rho^{2}(\varphi)d\lambda^{2}=k(\varphi,\lambda)(dx^{2}+dy^{2})$

où 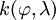$k(\varphi,\lambda)$ est une fonction. La convention $x = λ$ implique que 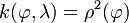$k(\varphi,\lambda)=\rho^{2}(\varphi)$ et

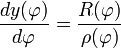
$\frac{d y(\varphi)}{d\varphi}=\frac{R(\varphi)}{\rho(\varphi)}$

Bien que nous n'en ayons pas besoin dans la suite, cette équation différentielle s'intègre sans grande difficulté (voir déroulé, on trouve l'expression des coordonnées conformes de Mercator généralisées :

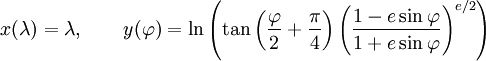$x(\lambda)=\lambda,\qquad y(\varphi)=\ln\left(\tan\left(\frac{\varphi}{2} +\frac{\pi}{4}\right)\left(\frac{{1-e\sin\varphi}}{{1+e\sin\varphi}}\right)^{e/2}\right)$

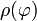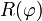Expressions de $\rho(\varphi)$ et de $R(\varphi)$ et détails de l'intégration

La représentation paramètrique ad-hoc de l'ellipse qui est utilisée pour l'ellipsoïde terrestre dans les systèmes de projection Mercator aussi bien que Lambert et UTM est

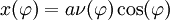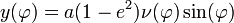
$x(\varphi)=a\nu(\varphi)\cos(\varphi)$ , $y(\varphi)=a(1-e^{2})\nu(\varphi)\sin(\varphi)$

respectivement la distance au petit axe de l'ellipse 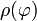$\rho(\varphi)$ , l'axe Nord Sud en l'occurrence et la distance au grand axe, en l'occurrence la distance au plan équatorial avec

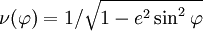
$\nu(\varphi)=1/\sqrt{1-e^{2}\sin^{2}\varphi}$

On vérifie sans peine que avec $b 2 / a 2 = 1 - e 2$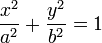

$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$

On vérifie aussi sans peine que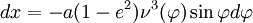

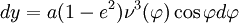
$dx=-a(1-e^{2})\nu^{3}(\varphi)\sin\varphi d\varphi$ et $dy=a(1-e^{2})\nu^{3}(\varphi)\cos\varphi d\varphi$

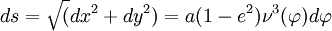et ainsi que $\varphi$ est bien la latitude, angle formé par la normale à l'ellipse avec le grand axe. Si on regarde l'élément différentiel d'arc on trouve $ds=\sqrt{(}dx^{2}+dy^{2})=a(1-e^{2})\nu^{3}(\varphi)d\varphi$ ce qui nous donne accès au rayon de courbure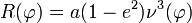 $R(\varphi)=a(1-e^{2})\nu^{3}(\varphi)$

Quelques indications pour intégrer l'équation différentielle ( [eq:Differentiel-Mercator])

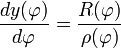
Soit $\frac{dy(\varphi)}{d\varphi}=\frac{R(\varphi)}{\rho(\varphi)}$

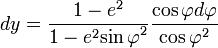
qui s'écrit aussi bien $dy=\frac{1-e^{2}}{1-e^{2}{\sin\varphi}^{2}}\frac{\cos\varphi d\varphi}{{\cos\varphi}^{2}}$

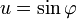
et en posant $u=\sin\varphi$

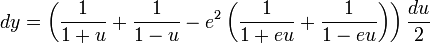
$dy=\left(\frac{1}{1+u}+\frac{1}{1-u}-e^{2}\left(\frac{1}{1+eu}+\frac{1}{1-eu}\right)\right)\frac{du}{2}$

Un petit calcul montre que 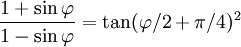$\frac{1+\sin\varphi}{1-\sin\varphi}=\tan(\varphi/2+\pi/4)^{2}$ et on arrive au résultat ([eq:Mercator]).

Etape 2: des coordonnées de Mercator généralisées (x,y) vers les coordonnées UTM (E,N)

La deuxième étape est une transformation conforme des coordonnées conformes de Mercator généralisées x,y vers les coordonnées UTM X,Y.

On utilise la propriété qu'une telle transformation conforme s'écrit à l'aide d'une fonction analytique en variables complexes 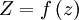$Z=f\left(z\right)$ avec $Z = Y + i X$ et $z = y + i x$ .

Sans perte de généralité on suppose que le méridien de référence est en $x = λ = 0$ . Par convention, les coordonnées UTM sont telles que sur le méridien de référence est en $X = 0$ et le long de celui ci $Y$ mesure la distance, c'est à dire que 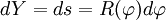$dY=ds=R(\varphi)d\varphi$ . On intègre cette dernière équation pour obtenir 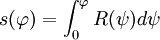$s(\varphi)=\int_{0}^{\varphi}R(\psi)d\psi$ qui est la distance entre le point de latitude $\varphi$ et l'équateur (C'est intégrale elliptique de première espèce, mais nous ne l'utiliserons pas). Sur le méridien de référence on a donc:

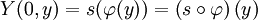
$Y(0,y)=s(\varphi(y))=\left(s\circ\varphi\right)\left(y\right)$

et l'on déduit par prolongement analytique que

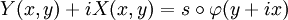
$Y(x,y)+iX(x,y)=s\circ\varphi(y+ix)$

Dans une carte de Mercator transverse, on s'éloigne peu du méridien de référence $x = 0$ . On peut donc utiliser un développement limité par rapport à la variable $x = λ$ , en $x = 0$ :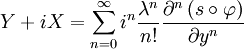

$Y+iX=\sum_{n=0}^{\infty}i^{n}\frac{\lambda^{n}}{n!}\frac{\partial^{n}\left(s\circ\varphi\right)}{\partial y^{n}}$

en identifiant parties réelles et imaginaires on obtient: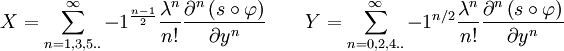

$X=\sum_{n=1,3,5..}^{\infty}-1^{\frac{n-1}{2}}\frac{\lambda^{n}}{n!}\frac{\partial^{n}\left(s\circ\varphi\right)}{\partial y^{n}}\qquad Y=\sum_{n=0,2,4..}^{\infty}-1^{n/2}\frac{\lambda^{n}}{n!}\frac{\partial^{n}\left(s\circ\varphi\right)}{\partial y^{n}}$

La première dérivée se calcule facilement en utilisant des relations précédentes:

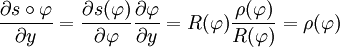
$\frac{\partial s\circ\varphi}{\partial y}=\frac{\partial s(\varphi)}{\partial\varphi}\frac{\partial\varphi}{\partial y}=R(\varphi)\frac{\rho(\varphi)}{R(\varphi)}=\rho(\varphi)$

La dérivée seconde s'obtient en dérivant la précédente de la même manière.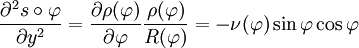

$\frac{\partial^{2}s\circ\varphi}{\partial y^{2}}=\frac{\partial\rho(\varphi)}{\partial\varphi}\frac{\rho(\varphi)}{R(\varphi)}=-\nu(\varphi)\sin\varphi\cos\varphi$

En continuant ainsi jusqu'à l'ordre $n = 6$ , en se limitant au premier ordre en $e' 2 = e 2 / (1 - e 2)$ et en utilisant les notations précédentes, on obtient finalement: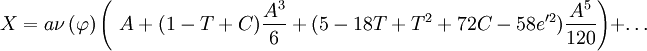

$X=a\nu\left(\varphi\right)\left(\ A+(1-T+C)\frac{A^{3}}{6}+(5-18T+T^{2}+72C-58e'^{2})\frac{A^{5}}{120}\right)+\ldots$

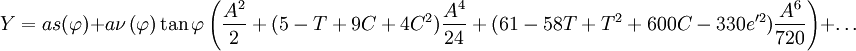
$Y=as(\varphi)+a\nu\left(\varphi\right)\tan\varphi\left(\frac{A^{2}}{2}+(5-T+9C+4C^{2})\frac{A^{4}}{24}+(61-58T+T^{2}+600C-330e'^{2})\frac{A^{6}}{720}\right)+\ldots$

Pour finir, les coordonnées UTM $N, E$ ne sont pas exactement $X, Y$ , mais par convention elles sont réduites et décalées:

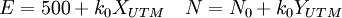
$E=500+k_{0}X_{UTM}\quad N=N_{0}+k_{0}Y_{UTM}$

avec le facteur de réduction $k 0 = 0.9996$ et $N 0$ a été donné plus haut.

Etape 3: Des coordonnées de Mercator généralisé aux coordonnées Lambert

Les projection de Lambert et de Mercator sont conformes, il y a donc une transformation conforme plan sur plan qui passe de Mercator à Lambert et une fonction analytique associée que nous allons justifier: 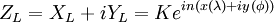$Z_L=X_L+iY_L=Ke^{in\left(x(\lambda)+iy(\phi)\right)}$ ou $K$ et $n$ sont deux paramètres réels et ou $x (λ)$ et $y (φ)$ sont les coordonnées Mercator. En coordonnées polaires, c'est à dire en posant $X L + i Y L = ρ(φ) i θ(λ)$ , cela donne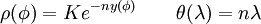 $\rho(\phi)=Ke^{-ny(\phi)}\qquad \theta(\lambda)=n\lambda$

Ainsi les méridiens $λ$ constant sont des rayons et les parallèles $φ$ constant deviennent les arcs de cercles concentriques qui forment avec les rayons un réseau orthogonal. Cette carte est le développé d'un cône dont le sommet est l'image d'un pôle. Lambert est précisée par l'exigence que les longueurs soient respectées sur deux parallèles sécants dits automécoïques $φ 1$ et $φ 2$ . Sur le terrain ces longueurs sont $2π a ν(φ 1)cosφ 1$ et $2π a ν(φ 2)cosφ 2$ qui doivent être égales à la longueur sur la carte Lambert $2π n ρ(φ 1)$ et $2π n ρ(φ 2)$ d'ou les deux équations : $2\pi a\nu(\phi_1)\cos\phi_1=2\pi n Ke^{-ny(\phi_1)}\qquad 2\pi a\nu(\phi_2)\cos\phi_2=2\pi n Ke^{-ny(\phi_2)}$

Ce qui donne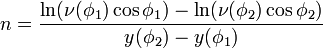 $n={{\ln(\nu(\phi_1)\cos\phi_1)-\ln(\nu(\phi_2)\cos\phi_2)}\over{y(\phi_2)-y(\phi_1)}}$ et $K$ s'en déduit par substitution dans l'une ou l'autre des égalités précédentes.

A partir des expressions des coordonnées polaires et en prenant l'origine à l'intersection du méridien et du parallèle de référence on retrouve les coordonnées Lambert.

Voir aussi

Système géodésique

Longitude

Latitude

Altitude

Projection cartographique

Références

(en) Rapport gouvernemental américain sur la définition officielle de la projection UTM utilisée aux États-Unis

(en) Convertisseur de coordonnées géodésiques et UTM

(fr) Localisation spatiale: Projections, systèmes de coordonnées

Ce document provient de « Transverse Universelle de Mercator ».

Catégories : Géodésie | Projection cartographique

Contenu soumis à la licence CC-BY-SA. Source : Article Transverse Unverselle de Mercator de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts