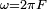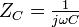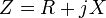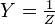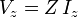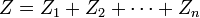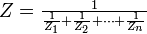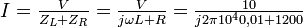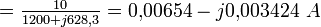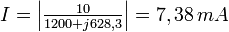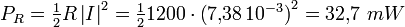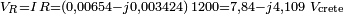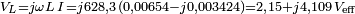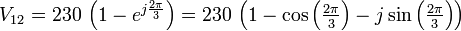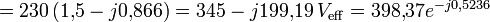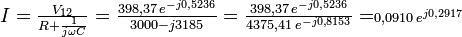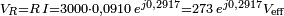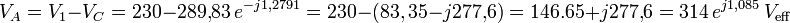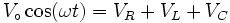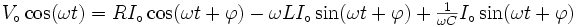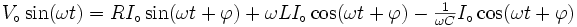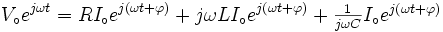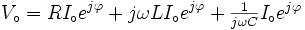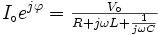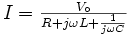Transmutation complexe

Transmutation complexe

Impédance (électricité)

Page d'aide sur l'homonymie Pour les articles homonymes, voir Impédance.

L'impédance électrique mesure l'opposition d'un circuit électrique au passage d'un courant alternatif sinusoïdal. La définition d'impédance est une généralisation de la loi d'Ohm dans l'étude des circuits en courant alternatif.

Le mot impédance fut inventé par Oliver Heaviside en juillet 1886. Il vient du verbe anglais to impede signifiant "retenir", "faire obstacle à" ; verbe qui dérive lui-même du latin impedire qui veut dire "entraver".

Dans un circuit formé par des résistances, condensateurs et bobines, toutes les tensions et les courants sont solutions d'équations différentielles. Mais, si toutes les sources délivrent des courants et des tensions fonctions sinusoïdales du temps de même fréquence et d'amplitude constante, les solutions, à l'état stationnaire (quand tous les phénomènes transitoires se sont estompés), sont également des fonctions sinusoïdales de même fréquence que les sources et dont l'amplitude et la phase à l'origine du temps sont constantes.

Le formalisme des impédances établit quelques règles de calculs des potentiels et des intensités du courant en tout point d'un circuit alimenté par diverses sources et comportant des éléments inductifs et capacitifs. Les méthodes de calcul sont alors similaires à celles utilisées pour les circuits en courant continu. Ce qui montre l'avantage d'employer les impédances.

Ces règles ne sont valables que :

  • En régime sinusoïdal établi, c’est-à-dire, avec des sources de tension et de courant sinusoïdales et une fois les phénomènes transitoires de départ disparus.
  • Avec des composants linéaires, c’est-à-dire, des composants dont l'équation caractéristique (relation entre la tension à leurs bornes et l'intensité du courant qui les traverse) est une équation différentielle à coefficients constants. Des composants non linéaires comme les diodes sont exclus. Les bobines à noyau ferromagnétique donneront seulement des résultats approchés et ce, à condition de ne pas dépasser les valeurs d'intensité au dessus de laquelle leur fonctionnement ne peut plus être considéré comme linéaire suite à la saturation qui intervient dans ces matériaux.

Si toutes les sources n'ont pas la même fréquence ou si les signaux ne sont pas sinusoïdaux, on peut décomposer le calcul en plusieurs étapes à chacune desquelles on pourra utiliser le formalisme d'impédances. Voir plus loin dans cet article.

Sommaire

Définitions

Impédance

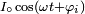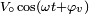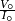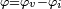Soit un composant électrique ou un circuit alimenté par un courant sinusoïdal \scriptstyle{I_\circ\cos(\omega t+ \varphi_i)} \,. Si la tension à ses bornes est \scriptstyle{V_\circ\cos(\omega t + \varphi_v)} \, , l'impédance du circuit ou du composant est définie comme un nombre complexe Z, dont le module est égal au rapport \scriptstyle{V_\circ\over I_\circ} \, et dont l'argument est égal à \scriptstyle{\varphi} = \scriptstyle{\varphi_v} - \scriptstyle{\varphi_i}\,.

\begin{matrix} &|Z| &={V_\circ\over I_\circ} \\ arg&(Z)&=\varphi_v - \varphi_i = \varphi \end{matrix} \,


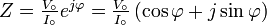
soit Z= \textstyle{{V_\circ\over I_\circ}}e^{j\varphi}= \textstyle{{V_\circ\over I_\circ}}\left( \cos\varphi + j\sin\varphi\right)

Comme les tensions et les courants sont sinusoïdaux, on peut utiliser aussi bien des valeurs crête (des amplitudes), des valeurs efficaces ou des valeurs crête à crête. Mais il faut faire bien attention à rester uniforme et de ne pas les mélanger. Les résultats des calculs seront du même type que celui utilisé pour les sources.

L'impédance se mesure en ohms.

Module de l'impédance

Remarque : souvent, par abus de langage on désigne par le terme impédance ce qui, en toute rigueur, devrait s'appeler module de l'impédance.

Le module de l'impédance se mesure en ohms.

Impédance des composants de base

Composants parfaits :

  • Résistance: l'impédance d'une résistance R est égale à R :
Z_R= R\, .
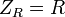C'est le seul composant à avoir une impédance réelle.
  • Bobine: L'impédance d'une bobine d'inductance L est :
Z_L= j\omega L \,.
Ici \scriptstyle{\omega} = 2\pi F est la pulsation, F la fréquence et j² = -1.
  • Condensateur: L'impédance d'un condensateur de capacité C est :
Z_C=\textstyle{{1\over j\omega C}}\,

Les composants réels ont des impédances plus compliquées et sont modélisés par des circuits constitués de composants idéaux. Par exemple, un résistor réel présente, en général, une inductance en série avec sa résistance. Une résistance bobinée ressemble à s'y méprendre à une inductance et elle présente une valeur d'inductance significative. De même, un condensateur et une bobine réels peuvent être modélisés en ajoutant une résistance en série ou en parallèle avec la capacité ou l'inductance pour tenir compte des défauts et pertes. Il faut même parfois ajouter des inductances au modèle du condensateur et des capacités au modèle d'inductance. Ces composantes parasites de l'impédance influent significativement sur l'impédance basique au delà d'une fréquence qui peut varier de quelques kiloHertz à quelques gigaHertz.

Réactance

Une impédance peut être représentée comme la somme d'une partie réelle plus une partie imaginaire :

Z= R+jX \,

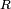\scriptstyle{R} est la partie résistive et 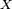\scriptstyle{X} est la partie réactive ou réactance.

Admittance

Voir article principal admittance. L'admittance est l'inverse de l'impédance :

Y= \textstyle{1\over Z}

La conductance est la partie réelle de l'admittance et la susceptance est la partie imaginaire de l'admittance. L'admittance, la conductance et la susceptance se mesurent en siemens. Un siemens est l'inverse d'un ohm.

Sources de tension ou de courant déphasées

Si, dans un circuit, on a plusieurs sources de tension ou de courant, on choisit une d'entre elles comme source de référence de phase. Par exemple, si la source prise comme référence est de la forme 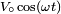\scriptstyle{V_\circ\cos(\omega t) } , on écrira sa tension comme 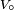\scriptstyle{V_\circ} . 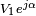Si la tension d'une autre source est en avance de phase d'un angle \scriptstyle{\alpha} par rapport à la source de référence, on écrira cette tension comme \scriptstyle{V_1e^{j\alpha}} . L'argument des tensions ou courants calculés donnera leur avance de phase par rapport à la source de référence. 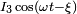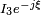Ainsi, par exemple une source de courant est \scriptstyle{I_3\cos(\omega t - \xi)} s'écrira sous la forme \scriptstyle{I_3e^{-j\xi}} .

Diagramme de Fresnel

Article détaillé : Représentation de Fresnel.

On peut représenter les tensions des sources et les tensions aux bornes des composants d'un circuit comme des vecteurs dans le plan complexe. Avec un peu d'habitude et un minimum de connaissances de géométrie, ces dessins sont beaucoup plus explicites que les valeurs ou des formules. Évidemment ces représentations ne sont pas un moyen de calcul, mais un moyen de « voir » comment les tensions s'additionnent. Ils peuvent être aussi un moyen d'écrire les formules finales en partant des propriétés géométriques. Vous trouverez deux exemples de diagrammes de Fresnel dans les exemples plus bas.

Calcul de circuits avec les impédances

Avec ce qui vient d'être dit, on peut calculer des circuits comprenant des impédances de manière similaire a celle utilisée pour le calcul avec des résistances en courant continu.

Lois de Kirchhoff

Les lois de Kirchhoff s'appliquent de la même manière: « la somme des courants arrivant sur un nœud est nulle » et « la somme des tensions autour d'une maille est nulle ». Cette fois, aussi bien les courants que les tensions sont représentés par des nombres complexes. (Voir transformation complexe).

Généralisation de la loi d'Ohm

La tension aux bornes d'une impédance est égale au produit de l'impédance par le courant :

V_z=Z\,I_z\,

Aussi bien l'impédance que le courant et la tension sont, en général, complexes.

Impédances en série ou en parallèle

Les impédances en série ou en parallèle se traitent comme les résistances avec la loi d'Ohm. L'impédance de plusieurs impédances en série est égale à leur somme :

Z = Z_1+Z_2 + \cdots + Z_n

L'impédance de plusieurs impédances en parallèle est égale à l'inverse de la somme de leurs inverses :

Z=\textstyle{1 \over \scriptstyle{{1\over Z_1}+{1\over Z_2}+\cdots +{1\over Z_n}}}

Interprétation des résultats

Le résultat du calcul d'une tension ou d'un courant est, en général, un nombre complexe. Ce nombre complexe s'interprète de la façon suivante :

  • Le module indique la valeur de la tension ou du courant calculé. Si les valeurs utilisées pour les sources étaient des valeurs crête, le résultat sera aussi une valeur crête. Si les valeurs utilisées étaient des valeurs efficaces, le résultat sera aussi une valeur efficace.
  • L'argument de ce nombre complexe donne le déphasage par rapport à la source utilisée comme référence de phase. Si l'argument est positif, la tension ou le courant calculés seront en avance de phase.

Exemples

Une seule source

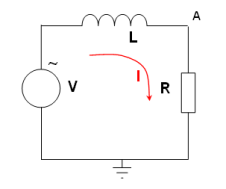Inductance et résistance en série alimentées par une source sinusoïdale.

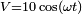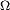Dans le diagramme de droite nous avons une source sinusoïdale \scriptstyle{V=10\cos(\omega t)} de 10 volts d'amplitude et de 10 kHz de fréquence. En série nous avons une inductance de 10 mH et une résistance de 1,2 k\scriptstyle{\Omega} .
Calculons le courant \scriptstyle{I} qui circule dans le circuit :

I =\textstyle{{V\over Z_L + Z_R}={V\over j\omega L + R}={10\over j2\pi 10^4 0,01 + 1200} }
\textstyle{={10\over 1200 + j628,3}}=0{,}00654-j0{,}003424\,\, A

Le module de ce courant sera :

I =\left|\textstyle{{10\over 1200 + j628,3}}\right|=7,38\,mA

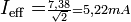
Comme la tension était en valeur crête (amplitude), le courant obtenu l'est aussi. Le courant efficace est I_\mathrm{eff}=\scriptstyle{{7,38\over\sqrt{2} }}=5,22 mA
La phase du courant est l'argument du nombre complexe :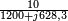 \scriptstyle{{10\over 1200 + j628,3}}  :

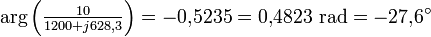\mathrm{arg}\left(\textstyle{{10\over 1200 + j628,3}}\right)= -0{,}5235 = 0{,}4823 \,\, \mathrm{rad} = -27{,}6^\circ.

Le courant est en retard de phase par rapport à la tension d'alimentation. Ceci est logique puisque le circuit est inductif.

Diagramme de Fresnel d'une bobine et une résistance en série. Le cercle en gris ne sert que comme aide au dessin de l'angle droit entre la tension sur la résistance et l'inductance.

Seule la résistance dissipe de la puissance :

P_R= \textstyle{1\over 2}R\left|I\right|^2=\textstyle{1\over 2}1200\cdot\left(7{,}38\,10^{-3}\right)^2=32{,}7\,\,mW

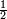Le \scriptstyle{1\over2} apparaît parce que la valeur du courant utilisée est la valeur crête.

La tension aux bornes de la résistance est :

\scriptstyle{V_R=I\,R=(0{,}00654-j0{,}003424)\,1200=7{,}84-j4{,}109 \,\,V_\mathrm{crete}}

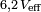
La tension efficace que l'on lirait sur un voltmètre serait le module de cette tension, divisé par racine de 2 : \scriptstyle{6{,}2\, V_\mathrm{eff}}

La tension aux bornes de l'inductance est :

\scriptstyle{V_L=j\omega L\,I\,=j628{,}3\,(0{,}00654-j0{,}003424)= 2{,}15+j4{,}109\, V_\mathrm{eff}}

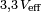
La tension efficace lue avec un voltmètre serait : \scriptstyle{3,3\, V_\mathrm{eff} }

On peut constater que l'addition de deux tensions « complexes » donne bien (aux arrondis près) la tension d'alimentation. Par contre, l'addition de deux tensions lues avec le voltmètre donne une tension plus élevée que celle de l'alimentation ( 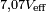\scriptstyle{7,07 V_\mathrm{eff}} ). C'est le résultat typique des mesures faites avec un voltmètre sur des circuits dont les tensions ne sont pas en phase.

Deux sources déphasées

Condensateur et résistance en série entre deux sources sinusoïdales déphasées.

Dans le circuit de droite, un condensateur de 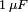\scriptstyle{1\,\mu F} et une résistance 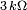\scriptstyle{3\,k\Omega} en série, sont branchés entre deux sources sinusoïdales. Nous prenons comme sources deux phases du réseau triphasé. La source de gauche sera notre source de référence. 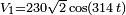\scriptstyle{V_1=230\sqrt{2}\cos(314\,t)} . celle de droite est en avance de phase de 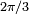\scriptstyle{2\pi/3} . Donc 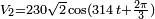\scriptstyle{V_2=230\sqrt{2}\cos(314\,t + {2\pi\over 3})} . 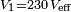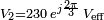Avec le formalisme d'impédances, la source de gauche s'écrira \scriptstyle{V_1=230\,V_\mathrm{eff}} et la source de droite s'écrira \scriptstyle{V_2=230\,e^{j{2\pi\over 3}}\,V_\mathrm{eff}} .

Commençons par calculer la différence de tension entre les deux sources :

\textstyle{V_{12}=230\,\left(1- e^{j{2\pi\over 3}}\right) =230\,\left(1-\cos\left(\textstyle{{2\pi\over 3}}\right)-j\sin\left(\textstyle{{2\pi\over 3}}\right)\right)}\,
\textstyle{=230\,(1{,}5-j0{,}866)=345-j199{,}19\, V_\mathrm{eff}=398{,}37 e^{-j0{,}5236}}\,

Le module de cette tension est 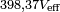\scriptstyle{398{,}37 V_\mathrm{eff}} , et elle est en retard de 0,5236 radians (30°) par rapport à la tension de référence.

Diagramme de Fresnel correspondant au deuxième exemple. Le premier cercle sert de guide pour les tensions de deux sources. Le second pour l'angle droit entre la tension du condensateur et celle de la résistance.

Le courant qui circule est :

\textstyle{I = {V_{12}\over R +\scriptstyle{1\over j\omega C}} = {398{,}37\,e^{-j0{,}5236}\over {3000 - j3185}}= {398{,}37\, e^{-j0{,}5236}\over 4375{,}41\, e^{-j0{,}8153}}= \scriptstyle{0{,}0910}\, e^{j0{,}2917}}

Comme les valeurs de départ étaient des valeurs efficaces, le courant aussi est une valeur efficace de 91 mA et en avance de phase de 16,71° par rapport à la tension de référence.

La tension aux bornes de la résistance est :

\scriptstyle{V_R=R\,I=3000\cdot 0{,}0910\, e^{j0{,}2917}=273\, e^{j0{,}2917}V_\mathrm{eff} }

La tension aux bornes du condensateur est :

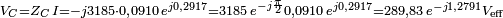\scriptstyle{V_C=Z_C\,I=-j3185\cdot 0{,}0910\, e^{j0{,}2917}=3185\, e^{-j{\pi\over 2}}0{,}0910\, e^{j0{,}2917}=289{,}83\, e^{-j1{,}2791}V_\mathrm{eff} } .

La tension aux bornes du condensateur est en retard de phase de 73,3° par rapport à la tension de référence. Comme précédemment, l'addition des modules des tensions (celles que l'on mesurerait avec un voltmètre) sur la résistance et le condensateur (563 V) est supérieure à la tension appliquée (398 V).

La tension au point A du circuit sera :

V_A= V_1-V_C=230 -289{,}83\, e^{-j1{,}2791}= 230 - (83,35-j277{,}6)=146.65+j277{,}6 = 314\,e^{j1{,}085} \,V_\mathrm{eff}

La tension au point A est plus élevée que la tension de chacune des sources.

Quand les impédances ne sont pas directement utilisables

Si toutes les sources n'ont pas la même fréquence, le formalisme des impédances n'est pas directement utilisable. Dans ce cas on peut utiliser le théorème de superposition et faire un calcul séparé pour chacune des fréquences (en remplaçant chaque source de tension de fréquence différente par un court-circuit et chaque source de courant de fréquence différente par un circuit ouvert). Chacune des tensions et courants totales du circuit sera la somme de chacune des tensions ou courants obtenus pour chacune des fréquences. Pour faire ces dernières sommes, il faut exprimer chacune des tensions obtenus avec leur dépendance avec le temps et leur déphasage : 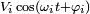\scriptstyle{V_i\cos(\omega_i t+\varphi_i)} pour les tensions et des formules similaires pour les courants.

Si les signaux ne sont pas sinusoïdaux mais qu'ils sont périodiques et continus, on peut décomposer les signaux en série de Fourier et utiliser le théorème de superposition et faire un calcul séparé pour chacune des fréquences du développement. Le résultat final sera la somme des résultats obtenus pour chacune des fréquences (avec leur dépendance temporelle et leur déphasage).

Origine des impédances

Quiconque a, un jour, reçu une décharge électrique, peut affirmer qu'elle était bien réelle et qu'elle n'avait rien d'imaginaire. Alors, d'où sort le j des formules d'impédances? Nous allons essayer de l'illustrer en calculant, sans utiliser le formalisme des impédances, le courant qui circule par un circuit formé par une résistance, une inductance et un condensateur en série.

Le circuit sera alimenté par une tension sinusoïdale et nous avons attendu assez longtemps pour que tous les phénomènes transitoires du début se soient estompés. Nous sommes en régime permanent. Comme le système est linéaire, le courant du régime permanent sera aussi sinusoïdal et aura la même fréquence que la source originale. La seule chose que nous ignorons est son amplitude et le déphasage que le courant peut avoir par rapport à la tension d'alimentation. 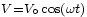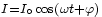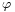Ainsi, si la tension d'alimentation est \scriptstyle{V=V_\circ\cos(\omega t)} le courant sera de la forme \scriptstyle{I=I_\circ\cos(\omega t+\varphi)}, où \scriptstyle{\varphi} est le déphasage que nous ne connaissons pas. L'équation à résoudre sera :

V_\circ\cos(\omega t)= V_R+V_L+V_C

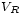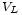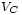où \scriptstyle{V_R}, \scriptstyle{V_L} et \scriptstyle{V_C} sont les tensions aux bornes de la résistance, l'inductance et le condensateur.

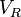V_R\, est égale à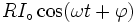 RI_\circ\cos(\omega t+\varphi)

La définition d'inductance nous dit que :

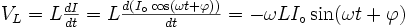V_L=L\textstyle{{dI\over dt}}= L\textstyle{{d\left(I_\circ\cos(\omega t+\varphi)\right)\over dt}}= -\omega L I_\circ\sin(\omega t+\varphi).

La définition de condensateur nous dit que 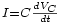\scriptstyle{I=C{dV_C\over dt}}. On peut vérifier (en intégrant l'expression) que :

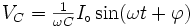V_C=\textstyle{{1\over \omega C}} I_\circ\sin(\omega t+\varphi) .

Ainsi, l'équation à resoudre est :

V_\circ\cos(\omega t)= RI_\circ\cos(\omega t+\varphi) -\omega L I_\circ\sin(\omega t+\varphi)+ \textstyle{{1\over \omega C}} I_\circ\sin(\omega t+\varphi)

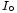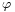C’est-à-dire, il faut trouver les valeurs de \scriptstyle{I_\circ} et de \scriptstyle{\varphi} qui satisfont cette unique équation pour toutes les valeurs du temps \scriptstyle{t}.

Imaginons maintenant que nous alimentons un circuit identique avec une autre source de tension sinusoïdale dont la seule différence est quelle commence avec un quart de période de retard. C’est-à-dire délivrant une tension égale à 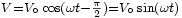\scriptstyle{V=V_\circ\cos(\omega t - {\pi \over 2} ) = V_\circ\sin(\omega t) }. La solution sera la même sauf qu'elle aura aussi le même retard. Le courant sera : 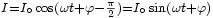\scriptstyle{I=I_\circ\cos(\omega t + \varphi - {\pi \over 2})= I_\circ\sin(\omega t + \varphi) }. L'équation de ce second circuit retardé sera:

V_\circ\sin(\omega t)= RI_\circ\sin(\omega t+\varphi) +\omega L I_\circ\cos(\omega t+\varphi)- \textstyle{{1\over \omega C}} I_\circ\cos(\omega t+\varphi)

Il y a des signes qui ont changé car le cosinus retardé se transforme en sinus, mais le sinus retardé se transforme en 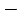\textstyle{\mathbf{-}}cosinus.
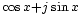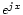Maintenant nous allons additionner les deux équations après avoir multiplié la seconde par j. L'idée est de pouvoir transformer les expressions de la forme \scriptstyle{\cos x+j\sin x} en \scriptstyle{e^{jx} }, utilisant les formules d'Euler. Le résultat est:

V_\circ e^{j\omega t} =RI_\circ e^{j\left(\omega t+\varphi\right)}+j\omega LI_\circ e^{j\left(\omega t+\varphi\right)} +\textstyle{{1\over j\omega C}}I_\circ e^{j\left(\omega t+\varphi\right)}

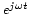Comme \scriptstyle{e^{j\omega t} } est différent de zéro,on peut diviser toute l'équation par ce facteur:

V_\circ =RI_\circ e^{j\varphi}+j\omega LI_\circ e^{j\varphi} +\textstyle{{1\over j\omega C}}I_\circ e^{j\varphi}

on déduit:

I_\circ e^{j\varphi}= \textstyle{V_\circ \over R + j\omega L + \scriptstyle{{1 \over j\omega C}}}

Le terme de gauche comprend les deux inconnues que nous voulions calculer: l'amplitude et la phase du courant. Son amplitude sera égale au module du nombre complexe de droite et sa phase sera égale à l'argument du nombre complexe de droite.

Mais le terme de droite est la formule habituelle à laquelle nous arrivons quand nous traitons les impédances des résistances, inductances et condensateurs de la même façon que l'on traite les résistances dans la loi d'Ohm. La formule est exactement celle nous nous écrivons quand nous utilisons le formalisme de impédances. On reconnaît au dénominateur les impédances de la résistance, l'inductance et le condensateur. Ce n'est pas inutile de repeter que quand nous écrivons:

I= \textstyle{V_\circ \over R + j\omega L + \scriptstyle{{1 \over j\omega C}}}

nous supposons que la personne qui lit cette formule sait l'interpréter et ne va pas croire que le courant puisse être complexe ou imaginaire. La même supposition est implicite quand nous retrouvons des expressions comme "nous alimentons avec une tension 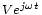\scriptstyle{Ve^{j\omega t}} " ou o "le courant est complexe".

Voir aussi

Électromagnétisme • Électricité • Électronique • Électrotechnique • Électrochimie • Automatique • Traitement du signal
Notions théoriques : Admittance • Capacité • Conductance • Courant • Impédance • Inductance • Résistance • Tension • Vitesse de l'électricité
Composant électrique : Accumulateur • Antenne • Capteur • Connecteur • Machine électrique • Pile
Circuit électrique • Économie • Histoire de l'électricité
Électromagnétisme • Électricité • Électronique • Électrotechnique • Électrochimie • Automatique • Traitement du signal
Électrostatique : Champ électrique • Charge électrique • Loi de Coulomb • Potentiel électrique
Magnétostatique : Champ magnétique • Moment magnétique • Loi de Biot et Savart
Électrocinétique : Champ électromagnétique • Courant de déplacement • Courant électrique • Ampère • Équations de Maxwell • Force électromotrice • Force de Lorentz • Induction électromagnétique • Loi de Lenz-Faraday • Rayonnement électromagnétique
Magnétisme : Diamagnétisme • Paramagnétisme • Superparamagnétisme • Ferromagnétisme • Antiferromagnétisme • Ferrimagnétisme • Loi de Curie • Domaine de Weiss • Susceptibilité magnétique • Perméabilité magnétique
  • Portail de l’électricité et de l’électronique Portail de l’électricité et de l’électronique
  • Portail de la physique Portail de la physique
Ce document provient de « Imp%C3%A9dance (%C3%A9lectricit%C3%A9) ».

Wikimedia Foundation. 2010.

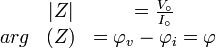
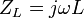Contenu soumis à la licence CC-BY-SA. Source : Article Transmutation complexe de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Liste d'œuvres et d'expositions de Gianfredo Camesi — Article principal : Gianfredo Camesi. Liste d œuvres et d expositions de Gianfredo Camesi, artiste peintre sculpteur suisse né le 24 mars 1940 à Cevio, canton du Tessin. Sommaire 1 Œuvres 1.1 Évolution d une recherche …   Wikipédia en Français

  • ALCHIMIE — L’alchimie a longtemps été confondue avec l’occultisme, la magie et même la sorcellerie. Au mieux, on la réduisait à un ensemble de techniques artisanales préchimiques ayant pour objet la composition des teintures, la fabrication synthétique des… …   Encyclopédie Universelle

  • ATOME — L’atome est le terme ultime de la division de la matière dans lequel les éléments chimiques conservent leur individualité. C’est la plus petite particule d’un élément qui existe à l’état libre ou combiné. On connaît 89 éléments naturels auxquels… …   Encyclopédie Universelle

  • Liste Des Expositions De Gianfredo Camesi — Liste d œuvres et d expositions de Gianfredo Camesi Article principal : Gianfredo Camesi. Liste d œuvres et d expositions de Gianfredo Camesi, artiste peintre sculpteur suisse né le 24 mars 1940 à Cevio, canton du Tessin. Sommaire 1 Œuvres 1 …   Wikipédia en Français

  • Liste Des Œuvres De Gianfredo Camesi — Liste d œuvres et d expositions de Gianfredo Camesi Article principal : Gianfredo Camesi. Liste d œuvres et d expositions de Gianfredo Camesi, artiste peintre sculpteur suisse né le 24 mars 1940 à Cevio, canton du Tessin. Sommaire 1 Œuvres 1 …   Wikipédia en Français

  • Liste des expositions de Gianfredo Camesi — Liste d œuvres et d expositions de Gianfredo Camesi Article principal : Gianfredo Camesi. Liste d œuvres et d expositions de Gianfredo Camesi, artiste peintre sculpteur suisse né le 24 mars 1940 à Cevio, canton du Tessin. Sommaire 1 Œuvres 1 …   Wikipédia en Français

  • Liste des expositions de gianfredo camesi — Liste d œuvres et d expositions de Gianfredo Camesi Article principal : Gianfredo Camesi. Liste d œuvres et d expositions de Gianfredo Camesi, artiste peintre sculpteur suisse né le 24 mars 1940 à Cevio, canton du Tessin. Sommaire 1 Œuvres 1 …   Wikipédia en Français

  • Liste des œuvres de Gianfredo Camesi — Liste d œuvres et d expositions de Gianfredo Camesi Article principal : Gianfredo Camesi. Liste d œuvres et d expositions de Gianfredo Camesi, artiste peintre sculpteur suisse né le 24 mars 1940 à Cevio, canton du Tessin. Sommaire 1 Œuvres 1 …   Wikipédia en Français

  • Liste des œuvres de gianfredo camesi — Liste d œuvres et d expositions de Gianfredo Camesi Article principal : Gianfredo Camesi. Liste d œuvres et d expositions de Gianfredo Camesi, artiste peintre sculpteur suisse né le 24 mars 1940 à Cevio, canton du Tessin. Sommaire 1 Œuvres 1 …   Wikipédia en Français

  • Alchimie — Jan van der Straet Le laboratoire de l alchimiste (1551) L alchimie est une discipline qui recouvre un ensemble de pratiques et de spéculations en rapport avec la transmutation des métaux[1 …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”