Transformation clarke

Transformation clarke

Transformée de Clarke

La transformée de Clarke, est un outil mathématique utilisé en électrotechnique afin de modéliser un système triphasé grâce à un modéle diphasé

Un système triphasé constitué de bobines et de courants déphasés entre eux de 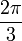\frac{2\pi}{3} permet de créer un champ tournant à la vitesse ω. Un système diphasé constitué de deux bobines perpendiculaires l'une par rapport à l'autre et parcourues par des courants déphasés entre eux de π / 2 permet de créer un champ tournant à la vitesse ω.

Sommaire

Matrice de transformation

Le but est de trouver les valeurs de xα et xβ à partir de xa , xb et xc. On peut modéliser le champ tournant créé par système triphasé par un système diphasé grâce aux transformations suivantes :


\begin{bmatrix} x_\alpha\\ x_\beta \end{bmatrix} = C_{23} \begin{bmatrix} x_a\\ x_b\\ x_c \end{bmatrix} \quad et \quad \begin{bmatrix} x_a\\ x_b\\ x_c \end{bmatrix} = C_{32} \begin{bmatrix} x_\alpha\\ x_\beta \end{bmatrix}

Pour résoudre ce système, l’axe 0a et 0α sont choisis parallèle à l’axe des réels. L’axe 0β est généralement choisi indirect par rapport à l’axe 0α . Ce n’est qu’une convention qui inverse les signes de la seconde colonne.

Ainsi , \begin{bmatrix} 0_a\\ 0_b\\ 0_c \end{bmatrix} = \begin{bmatrix} 1\\ e^{j\frac{2\pi}{3}}\\ e^{-j\frac{2\pi}{3}} \end{bmatrix} \quad et \quad \begin{bmatrix} 0_{\alpha}\\ 0_{\beta} \end{bmatrix} = \begin{bmatrix} 1\\ -j \end{bmatrix}

Trouver les matrices C32 et C23 revient à résoudre le système matriciel suivant : \begin{bmatrix} 1\\ -j \end{bmatrix} = C_{23} \begin{bmatrix} 1\\ e^{j\frac{2\pi}{3}}\\ e^{-j\frac{2\pi}{3}} \end{bmatrix} \quad et \quad \begin{bmatrix} 1\\ e^{j\frac{2\pi}{3}}\\ e^{-j\frac{2\pi}{3}} \end{bmatrix} = C_{32} \begin{bmatrix} 1\\ -j \end{bmatrix}

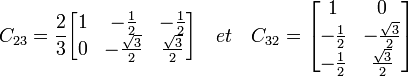Ce qui donne : C_{23} =\frac{2}{3} \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & -\frac{\sqrt{3}}{2} & \frac{\sqrt{3}}{2} \end{bmatrix} \quad et \quad C_{32} = \begin{bmatrix} 1 & 0 \\ -\frac{1}{2} & -\frac{\sqrt{3}}{2} \\ -\frac{1}{2} & \frac{\sqrt{3}}{2} \end{bmatrix} .

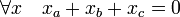
Avec \forall x\quad x_a+x_b+x_c=0

Il existe aussi une transformation de Concordia qui est la même que celle de Clarke mais qui est normée.

Électrotechnique

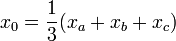Une composante homopolaire x0 est rajoutée afin de prendre en compte un système déséquilibré. La composante homopolaire est la somme des trois grandeurs divisée par trois dans la théorie des composants symétriques x_0 =\frac{1}{3}(x_a+x_b+x_c).

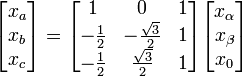
\begin{bmatrix} x_a \\ x_b \\ x_c \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1\\ -\frac{1}{2} & -\frac{\sqrt{3}}{2} & 1 \\ -\frac{1}{2} & \frac{\sqrt{3}}{2} & 1 \end{bmatrix} \begin{bmatrix} x_\alpha\\ x_\beta \\ x_0 \end{bmatrix}

Voir aussi

Liens internes

Liens externes

  • Portail de l’électricité et de l’électronique Portail de l’électricité et de l’électronique
Ce document provient de « Transform%C3%A9e de Clarke ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Transformation clarke de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Clarke — bezeichnet einen englischen Familiennamen, siehe Clarke (Familienname) einen Asteroid des Hauptgürtels, siehe (4923) Clarke den Codenamen eines Prozessors, siehe HP Saturn Clarke ist der Name folgender Orte: Château Clarke, ein französisches… …   Deutsch Wikipedia

  • Transformation de fortescue — Tout système de grandeurs triphasées déséquilibré peut se mettre sous la forme de la somme de trois systèmes équilibrés (ou symétriques) : Un système équilibré direct noté Gd. Un système équilibré inverse noté Gi. Un système de tension… …   Wikipédia en Français

  • Transformation des systemes triphases — Transformation des systèmes triphasés Les transformations des systèmes triphasés sont utilisées dans l étude des machines électriques. Ces transformations permettent : d établir le schéma monophasé équivalent d une machine électrique… …   Wikipédia en Français

  • Clarke-Transformation — Die Clarke Transformation, benannt nach Edith Clarke und auch als α,β Transformation bezeichnet, dient dazu, dreiphasige Größen wie bei einer Drehstrommaschine mit den Achsen U,V,W in ein einfacheres zweiachsiges Koordinatensystem mit den Achsen… …   Deutsch Wikipedia

  • Transformation de Clarke — Transformée de Clarke La transformée de Clarke, est un outil mathématique utilisé en électrotechnique afin de modéliser un système triphasé grâce à un modéle diphasé Un système triphasé constitué de bobines et de courants déphasés entre eux de… …   Wikipédia en Français

  • Transformation de Fortescue — Tout système de grandeurs triphasées déséquilibré peut se mettre sous la forme de la somme de trois systèmes équilibrés (ou symétriques) : un système équilibré direct noté Gd ; un système équilibré inverse noté Gi ; un système de… …   Wikipédia en Français

  • Transformation des systèmes triphasés — Les transformations des systèmes triphasés sont utilisées dans l étude des machines électriques. Ces transformations permettent : d établir le schéma monophasé équivalent d une machine électrique triphasée ; de faciliter la commande des …   Wikipédia en Français

  • D/q-Transformation — Die d/q Transformation, auch als dq , dq0 und als Park Transformation bezeichnet, dient dazu, dreiphasige Größen wie bei einer Drehstrommaschine mit den Achsen U,V,W in ein zweiachsiges Koordinatensystem mit den Achsen d und q zu überführen. Sie… …   Deutsch Wikipedia

  • Transformée de Clarke — La transformée de Clarke, est un outil mathématique utilisé en électrotechnique afin de modéliser un système triphasé grâce à un modéle diphasé Un système triphasé constitué de bobines et de courants déphasés entre eux de permet de créer un champ …   Wikipédia en Français

  • Operation Transformation (TV series) — Operation Transformation Format Lifestyle Created by Vision Independent Productions Starring Gerry Ryan (2008 …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”