Courant triphasé

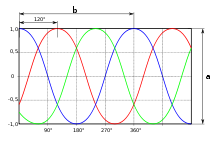
Graphique des trois tensions de même fréquence/amplitude et déphasées de 120°

Un système de courant (ou tension) triphasé est constituée de trois courants (ou tensions) sinusoïdaux de même fréquence de même amplitude qui sont déphasés entre eux (de 120 °, un tiers de tour ou ^2π⁄₃ radians dans le cas idéal). Si la fréquence est de 50 Hz par exemple, alors les trois phases sont retardées l'une par rapport à l'autre de ¹⁄₁₅₀ seconde (soit 6,6 ms). Lorsque les trois conducteurs sont parcourus par des courants de même valeur efficace, le système est dit équilibré.

Dans le cas de la distribution électrique, le réseau peut se modéliser par trois sources de tension d'amplitude identique, par exemple 230 V efficaces dans la plupart des pays européens. Cette tension est en principe constante, indépendante de la charge, seul le courant absorbé par chaque phase étant dépendant de la puissance de cette dernière.

Le courant triphasé permet d'éviter les problèmes de puissance inhérent au courant monophasé alternatif (en régime sinusoïdal). On peut démontrer que le courant triphasé délivre une puissance instantanée sans composante pulsée contrairement au courant monophasé où la puissance instantanée présente une variation sinusoïdale de fréquence double superposée à une composante continue^[1]. Il est absolument nécessaire d’annuler cette pulsation de la puissance car elle se retrouve également dans la puissance mécanique transmise par l'arbre de l'alternateur et se traduit par une pulsation du couple mécanique qui peut entrainer la destruction de ce dernier. De plus, les alternateurs triphasés ont un meilleur rendement que leurs homologues monophasés et le régime triphasé occasionne moins de pertes lors du transport en ligne de l'électricité.

Sommaire

1 Définitions de base
2 Distribution triphasée
3 Récepteurs triphasés
4 Intérêt du triphasé
- 4.1 Intérêt pour le transport de l'électricité
- 4.2 Intérêt pour la production de l'électricité
  - 4.2.1 De meilleurs alternateurs
  - 4.2.2 Annuler la puissance fluctuante
5 Transformation des systèmes triphasés
- 5.1 Transformation de Fortescue
6 Notes
7 Voir aussi
- 7.1 Articles connexes

Définitions de base

Grandeurs triphasées

Un système de grandeurs triphasées, généralement des tensions ou des courants électriques, peut se décrire par les équations :

$g_1 = G_1\sin\left( \omega t+\varphi_1\right)$

$g_2 = G_2\sin\left( \omega t+\varphi_1 - \tfrac23\pi\right)$

$g_3 = G_3\sin\left( \omega t+\varphi_1 + \tfrac23\pi\right)$

La [transformation complexe] permet d'associer à ces grandeurs des nombres complexes que l'on peut écrire sous la forme :

$g_1 = G_1e^{j \left( \omega t+\varphi_1\right)}$

$g_2 = G_2e^{j\left( \omega t+\varphi_1 - \tfrac23\pi\right)}$

$g_3 = G_3e^{j\left( \omega t+\varphi_1 + \tfrac23\pi\right)}$

qui est plus propice au traitement mathématique et décrit les [phaseur]s dans le plan complexe.

Systèmes triphasés équilibrés et déséquilibrés

Un système de grandeurs (tensions ou courants) triphasées est dit équilibré si les 3 grandeurs, fonctions sinusoïdales du temps, ont la même amplitude : $G 1 = G 2 = G 3 = G$

Il est aisé de vérifier qu'en l'occurrence,

u 1 + u 2 + u 3 = 0

Dans le cas contraire, le système triphasé est dit déséquilibré, et cette somme n'est plus nulle.

Systèmes triphasés directs et inverses

Si les 3 grandeurs passent par la valeur 0 dans l'ordre 1, 2, 3, 1, ..., le système triphasé est dit direct. Il peut alors se mettre sous la forme :

g 1 = G 1 sin(ω t + φ 1)

$g_2 = G_2\sin\left( \omega t+\varphi_1 - \tfrac23\pi \right)$

$g_3 = G_3\sin\left( \omega t+\varphi_1 - \tfrac43\pi\right) = G_3\sin\left( \omega t+\varphi_1 + \tfrac23\pi\right)$

Si les 3 grandeurs passent par la valeur 0 dans l'ordre 1, 3, 2, 1, ..., le système triphasé est dit inverse. Il peut alors se mettre sous la forme :

g 1 = G 1 sin(ω t + φ 1)

$g_2 = G_2\sin\left( \omega t+\varphi_1 + \tfrac23\pi \right)$

$g_3 = G_3\sin\left( \omega t+\varphi_1 + \tfrac43\pi\right) = G_3\sin\left( \omega t+\varphi_1 - \tfrac23\pi\right)$

Pour inverser l'ordre des phases, c'est-à-dire passer de l'ordre direct à l'ordre inverse et réciproquement, il faut inverser le branchement de deux phases.

Distribution triphasée

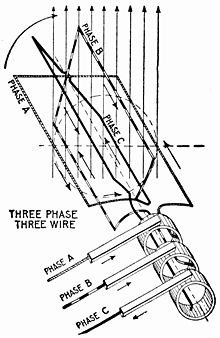
Animation d'un alternateur triphasé

Une distribution triphasée comporte 3 ou 4 fils

Trois conducteurs de phase dans le cas d'une charge équilibrée, c'est-à-dire qui consomme un courant identique sur chacune des trois phases. Tel est le cas par exemple des moteurs électriques triphasés.

Un conducteur de neutre qui n'est pas systématique mais qui est souvent distribué. Lorsqu'un appareil ne consomme pas un courant identique sur chacune des phases, un courant résiduel est produit, que le conducteur neutre permet d'évacuer afin de maintenir la tension nominale de distribution sur chacune des trois branches de la charge.

Les installations domestiques se font souvent en courant triphasé. Comme le courant consommé par chacune des phases est en général différent et varie dans le temps (mise en marche d'un lave-linge, d'une cuisinière, allumage et extinction de lumières ou d'appareils électroménagers...), l'installation électrique d'une maison d'habitation constitue une charge généralement déséquilibrée qui requiert la connexion du neutre. Si cette dernière devait être défectueuse, certains circuits de la maison pourraient recevoir une tension largement supérieure à leur tension nominale, avec des conséquences sérieuses pour les appareils qui y sont branchés et pour la sécurité de leurs utilisateurs.

Tensions simples

Les différences de potentiel entre chacune des phases et le neutre constituent un système de tensions triphasées notées généralement V (V_1N, V_2N, V_3N) et appelées tensions simples, tensions étoilées ou tensions de phase. Mathématiquement, on peut noter :

$v_1 = V_1\sqrt 2\sin( \omega t+\varphi_1)$

$v_2 = V_2\sqrt 2\sin\left( \omega t+\varphi_1 - \tfrac23\pi \right)$

$v_3 = V_3\sqrt 2\sin\left( \omega t+\varphi_1 - \tfrac43\pi\right)$

V_i la valeur efficace, ω la pulsation, φ_i la phase à l'origine et t le temps.

Dans le cas de distributions équilibrées, on a $V 1 = V 2 = V 3 = V$ .

Utilisant les nombres complexes et considérant une distribution équilibrée, cela s'écrit encore

$u_1 = V_{crete} e^{j\left( \omega t+\varphi_1\right)}$

$u_2 = V_{crete} e^{j\left( \omega t+\varphi_1 - \tfrac23\pi\right)}$

$u_3 = V_{crete} e^{j\left( \omega t+\varphi_1 + \tfrac23\pi\right)}$

en définissant la tension de crête

$V_{crete} = V \sqrt 2$

Tensions composées

Les différences de potentiel entre les phases constituent un système de tensions notées généralement U : (U₁₂, U₂₃, U₃₁) et appelées tensions composées ou tensions de ligne.

$u_{ij} = v_i - v_j = U_{ij}\sqrt 2\sin( \omega t+\varphi_{ij})$

Les tensions composées constituent un système de tensions triphasées si et uniquement si le système de tensions simples est un système équilibré. La somme des trois tensions composées est toujours nulle. Il en résulte que la composante homopolaire des tensions entre phases est toujours nulle (voir ci-dessous transformation de Fortescue).

Dans le cas de distributions équilibrées, on a : $U 12 = U 23 = U 31 = U$

Relation entre tensions simples et composées

Représentation de Fresnel des tensions simples et composées pour un système équilibré direct

Nous avons reporté sur la figure ci-contre le diagramme de Fresnel des tensions simples et composées délivrées par un système triphasé équilibré direct. L'origine du diagramme représente une tension nulle, celle du neutre. Dans un système équilibré, les tensions simples sont alors celles entre phase et neutre représentées en noir, et les tensions composées celles entre phases représentées en rouge. En observant, par exemple, le triangle isocèle formé par les tensions $v 1$ , $v 2$ et $u 12$ , nous pouvons remarquer que celui-ci a deux angles aigus de $π / 6$ radians (soit 30 degrés). On peut ainsi exprimer la valeur efficace de la tension composée $U$ en fonction de la valeur efficace de la tension simple $V$ à travers la relation :

$U = 2 \times V \times \cos(\pi/6)$

Il en va de même dans le cas d'un système équilibré indirect.

Par conséquent, dans un système triphasé équilibré, les valeurs efficaces des tensions simples et composées sont reliées par la relation :

$U = \sqrt 3 V$

Utilisant la notation complexe, le même résultat est obtenu:

$u_{12} = u_1 - u_2 = V_{crete}\sqrt 3e^{j \left( \omega t+\varphi_1+\tfrac\pi6\right)}$

$u_{23} = u_2 - u_3 = V_{crete}\sqrt 3e^{j\left( \omega t+\varphi_1 + \tfrac{3\pi}2\right)}$

$u_{31} = u_3 - u_1 = V_{crete}\sqrt 3e^{j\left( \omega t+\varphi_1 + \tfrac{5\pi}6\right)}$

avec

$V_{crete} = V\sqrt 2$

qui lie la tension efficace entre phase et neutre à sa valeur de crête.

Récepteurs triphasés

Un récepteur triphasé est constitué de trois dipôles aussi appelés enroulements ou phases. Si ces trois dipôles ont la même impédance, le récepteur est dit équilibré.

Un récepteur triphasé peut être relié à l'alimentation de deux manières :

La littérature anglophone désigne habituellement les couplages triangle et étoile par des noms de lettres :
- Triangle : Delta (Δ)
- Étoile : Wye (Y)

Un récepteur équilibré alimenté par un système équilibré de tensions absorbera trois courants de ligne formant également un système triphasé équilibré.

Intensités

Les courants de ligne ou courants composés sont notés $I$ . Les courants qui traversent les éléments récepteurs sont appelés courants de phase ou courants simples et sont notés $J$ .

Connexion d'un récepteur triphasé

Les trois dipôles qui constituent le récepteur triphasé sont reliés à 6 bornes conventionnellement disposées comme l'indique la figure ci-dessous.

L'avantage de cette disposition est de permettre la réalisation des deux couplages avec des barrettes d'égale longueur, la distance entre deux bornes contiguës étant constante. L'appareil est fourni avec trois barrettes identiques dont la longueur permet un câblage horizontal ou vertical. On doit utiliser ces barrettes de connexion afin de réaliser les couplages désirés :

Couplage étoile

Le couplage étoile des enroulements (couplage le plus fréquent) s'obtient en plaçant deux barrettes de connexions de la manière suivantes :

Couplage en étoile d'une plaque à bornes.png

Les trois bornes restantes seront câblées avec les trois conducteurs de phases.

Les trois bornes reliées ensemble par les deux barrettes constituent un point qui sera au potentiel du neutre. Ce point doit être relié au neutre de la distribution si l'appareil ne présente pas une charge équilibrée, ce qui est le cas par exemple d'une cuisinière électrique. Pour des machines électriques qui à l'instar des moteurs triphasés présentent une charge équilibrée, il est fortement déconseillé de connecter le neutre.

Dans un couplage étoile, les courants de ligne et de phase sont les mêmes, aussi on note :

I = J

Couplage triangle

Le couplage triangle des enroulements s'obtient en plaçant trois barrettes de connexions de la manière suivante :

Couplage en triangle d'une plaque à bornes.png

Un câble de phase est relié ensuite à chaque barrette. Le câble de neutre n'est pas connecté.

Dans un couplage triangle, il est nécessaire de décomposer chaque courant traversant les récepteurs. Ainsi, on a :

I 1 = J 21 - J 31

I 2 = J 23 - J 21

I 3 = J 23 - J 31

Les valeurs efficaces des courants de ligne et de phase sont liés par la relation :

$I = \sqrt 3 J$

Article connexe : théorème de Kennelly.

Plaques signalétiques des récepteurs triphasés

La plaque signalétique d'un récepteur triphasé précise la valeur des deux tensions entre phases permettant de l'alimenter :

Exemple

chauffe-eau : 230 V(1) / 400 V(2) :

La première valeur est la tension entre phase requise pour câbler le récepteur en étoile
La deuxième valeur est la tension entre phase requise pour câbler le récepteur en triangle^[2]

Puissance consommée par un récepteur triphasé

Puissance active

Le théorème de Boucherot impose que cela soit la somme des puissances consommées par chacun des dipôles :

en étoile : $P = V 1 I 1 cos φ 1 + V 2 I 2 cos φ 2 + V 3 I 3 cos φ 3$ soit, en régime équilibré : $P = 3 \cdot V I \cdot \cos \varphi(V;I)$

en triangle : $P = U 1 J 1 cos φ 1 + U 2 J 2 cos φ 2 + U 3 J 3 cos φ 3$ soit, en régime équilibré : $P = 3 \cdot U J \cdot \cos \varphi(U;J)$

Pour les récepteurs équilibrés et quel que soit le couplage, on peut écrire : $P =\sqrt 3 \cdot U I \cdot \cos \varphi$ .

Remarque : Dans ce cas, $φ$ n'est pas le déphasage entre $\underline U$ et $\underline I$ et la valeur $cos φ$ est appelé facteur de puissance.

Intérêt du triphasé

Autre vue d'un alternateur triphasé (Hawkins Electrical Guide, 1917)

Intérêt pour le transport de l'électricité

Le transport en triphasé permet d’économiser du câble et de diminuer les pertes par effet joule : trois fils de phases suffisent (le neutre n'est pas transporté, il est «recréé» au niveau du dernier transformateur). En effet, le déphasage entre chaque phase est tel que, pour un système équilibré, la somme des trois courants est supposée nulle (si les trois courants ont la même amplitude, alors $\cos(x) + \cos(x+\tfrac23\pi) + \cos(x+\tfrac43\pi)=0$ ). Et donc, en plus de faire l'économie d'un câble sur les longues distances, on économise en prime sur les effets joule (un câble supplémentaire traversé par un courant impliquerait des pertes supplémentaires).

Intérêt pour la production de l'électricité

De meilleurs alternateurs

L'alternateur triphasé s'est imposé dès l'origine (avant 1900) comme le meilleur compromis^[3].

Plus de 95 % de l’énergie électrique est générée par des alternateurs synchrones, des machines électromécaniques fournissant des tensions de fréquences proportionnelles à leur vitesse de rotation. Ces machines sont moins coûteuses et ont un meilleur rendement que les machines à courant continu (dynamos) qui délivrent des tensions continues (95 % au lieu de 85 %).

Les alternateurs (machines synchrones) triphasés qui produisent l'énergie électrique ont un meilleur rendement et un meilleur rapport poids/puissance qu'un alternateur monophasé de même puissance.

Annuler la puissance fluctuante

Supposons qu'un alternateur monophasé délivre 1 000 A sous une tension de 1 000 V et de fréquence 50 Hz. L'expression de la puissance délivrée se met sous la forme :

$P = U\sqrt 2\sin( \omega t) \cdot I\sqrt 2\sin( \omega t+\varphi)$

P = U I cos φ - U I cos(2ω t + φ)

Donc la puissance active délivrée (le premier terme de la somme) est comprise entre 0 et 1 MW (elle dépend du facteur de puissance de la charge), mais la puissance fluctuante (le deuxième terme de la somme) est une puissance sinusoïdale de fréquence 100 Hz et d’amplitude obligatoirement égale à 1 MW. La turbine, du fait de son inertie, tourne avec une vitesse mécanique quasi constante, et donc à chaque instant elle fournit une puissance identique. Ces différences de puissance se traduisent par des oscillations de couples qui sont, en majeure partie, absorbées par l’élasticité de l’arbre de transmission et finissent par provoquer sa destruction.

Pour supprimer cette puissance fluctuante, les alternateurs de grande puissance doivent donc nécessairement produire un système de tensions polyphasées : il faut produire n phases (n ≥ 2) déphasées convenablement dans le temps.

Par exemple en diphasé:

$P = U\sqrt 2\sin( \omega t) \cdot I\sqrt 2\sin( \omega t+\varphi)+U\sqrt 2 \cos( \omega t) \cdot I\sqrt 2 \cos( \omega t+\varphi)$

P = U I cos φ - U I cos(2ω t + φ) + U I cos φ + U I cos(2ω t + φ)

P = 2 U I cos φ

La puissance fluctuante a bien été annulée.

Le choix qui a été fait pour l'ensemble des réseaux du monde est n = 3.

Transformation des systèmes triphasés

Article détaillé : Transformation des systèmes triphasés.

Transformation de Fortescue

Article détaillé : Transformation de Fortescue.

Notes

Voir aussi

Regardez d'autres dictionnaires:

courant triphasé — trifazė srovė statusas T sritis automatika atitikmenys: angl. three phase current vok. Drehstrom, m; Dreiphasenstrom, m rus. трёхфазный ток, m pranc. courant triphasé, m … Automatikos terminų žodynas
courant triphasé — trifazė srovė statusas T sritis fizika atitikmenys: angl. three phase current vok. Drehstrom, m; Dreiphasenstrom, m rus. трёхфазный ток, m pranc. courant triphasé, m … Fizikos terminų žodynas
système à courant triphasé — trifazė sistema statusas T sritis automatika atitikmenys: angl. three phase system vok. Drehstromsystem, n; Dreiphasensystem, n rus. трёхфазная система, f pranc. système à courant triphasé, m; système triphasé, m … Automatikos terminų žodynas
ligne de transport à courant triphasé — trifazė elektros perdavimo linija statusas T sritis automatika atitikmenys: angl. three phase transmission line vok. Drehstromübertragungsleitung, f rus. линия электропередачи трёхфазного тока, f pranc. ligne de transport à courant triphasé, f … Automatikos terminų žodynas
redressement du courant triphasé — trifazis lyginimas statusas T sritis fizika atitikmenys: angl. three phase rectification vok. Dreiphasengleichrichtung, f rus. выпрямление трёхфазного тока, n pranc. redressement du courant triphasé, m … Fizikos terminų žodynas
triphasé — triphasé, ée [ trifaze ] adj. • 1892; de tri et phase ♦ À trois phases. Courant triphasé, dont les trois phases sont deux à deux décalées de 1/3 de période. ● triphasé, triphasée adjectif Se dit d un système de tensions ou de courants polyphasés… … Encyclopédie Universelle
Courant Alternatif — Pour les articles homonymes, voir Courant alternatif (revue). Le courant alternatif (qui peut être abrégé par CA, ou AC, pour Alternating Current en anglais, étant cependant souvent utilisé) est un courant électrique qui change de sens. Ce… … Wikipédia en Français
Courant électrique alternatif — Courant alternatif Pour les articles homonymes, voir Courant alternatif (revue). Le courant alternatif (qui peut être abrégé par CA, ou AC, pour Alternating Current en anglais, étant cependant souvent utilisé) est un courant électrique qui change … Wikipédia en Français
Courant alternatif — Pour les articles homonymes, voir Courant alternatif (revue). Le courant alternatif (qui peut être abrégé par CA, ou AC, pour Alternating Current en anglais, cependant souvent utilisé) est un courant électrique qui change de sens, il est tantôt… … Wikipédia en Français
Courant monophasé — Un courant monophasé est un courant électrique alternatif fourni au moyen d une ligne bifilaire. Il s oppose aux courants polyphasés, tels que le courant triphasé, pour lesquels plusieurs lignes sont utilisées et déphasées entre elles. Le courant … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Courant triphasé

Sommaire