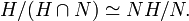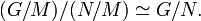Théorèmes d'isomorphismes

Théorèmes d'isomorphisme

En mathématiques, les trois théorèmes d'isomorphisme fournissent l'existence d'isomorphismes dans le cadre de la théorie des groupes.

Ces trois théorèmes d'isomorphisme sont généralisables à d'autres structures que les groupes. Voir notamment Algèbre universelle#Passage au quotient et théorèmes d'isomorphie.

Premier théorème d'isomorphisme

Proposition — Soient $G$ et $G'$ deux groupes et soit 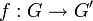$f:G \rightarrow G'$ un morphisme de groupes. Alors 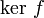$\ker \, f$ est un sous-groupe normal de $G$ .

Démonstration

Notons $.$ la loi de $G$ et $G'$ . On notera alors 1 l'élément neutre de $G$ et $G'$ .

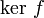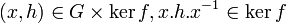Vérifions que $\ker \, f$ est stable par conjugaison, c'est-à-dire que si $(x, h) \in G\times \ker f, x . h . x^{-1} \in \ker f$ .

$f (x . h . x - 1) = f (x). f (h). f (x - 1)$

Comme 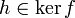$h \in \ker f$ , $f (h) = 1$ . Donc, $f (x . h . x - 1) = f (x). f (x - 1) = f (x . x - 1) = f (1) = 1$

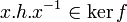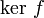D'où $x . h . x^{-1} \in \ker f \,$ et $\ker \, f$ est un sous-groupe normal de $G$ .

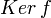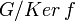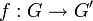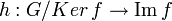Le fait que $Ker \, f$ soit un sous-groupe distingué de G permet de définir sur le groupe quotient $G / Ker \, f$ une loi compatible avec celle du groupe G. Grâce à cette compatibilité, le morphisme de groupes $f : G \rightarrow G'$ va permettre de définir l'isomorphisme $h : G / Ker \, f \rightarrow {\rm Im} \, f$ .

Premier théorème d'isomorphisme — Soient $G$ et $G'$ deux groupes, et soit 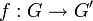$f:G \rightarrow G'$ un morphisme de groupes. Alors $f$ induit un isomorphisme de 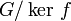$G/\ker\, f$ vers $f (G)$ .

Démonstration

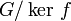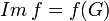Construisons l'application $h$ de $G/\ker \, f$ vers $Im \, f = f(G)$ .

$h$ est définie de la façon suivante :

pour $[x] \in G/\ker$ , $h ([x]) = f (x)$ où $x$ est un représentant de la classe d'équivalence $[x]$ .

$h$ est ainsi bien définie. En effet, soit $y$ un autre représentant de la classe d'équivalence $[x]$ , alors :

$h ([y]) = f (y) = f (x x - 1 y) = f (x) f (x - 1 y)$ .

Comme 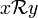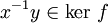$x \mathcal R y$ , $x^{-1} y \in \ker \, f$ et $f (x - 1 y) = 1$ . D'où $h ([y]) = f (x) = h ([x])$ .

Puisque la valeur de l'aplication h ne dépend pas du représentant choisi de la classe $[x]$ , cette application est bien définie.

Par définition, h est un morphisme de groupe.

Montrons que h est injective. Soient $[x]$ et $[y]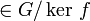$ $\in G/\ker \, f$ tels que $h ([x]) = h ([y])$ .

Donc $f (x) = f (y)$

$f (x) f (y) - 1 = 1$

$f (x y - 1) = 1$

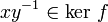$x y^{-1} \in \ker \, f$ .

Par définition de la classe d'équivalence sur 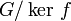$G/\ker \, f$ , on a $[x] = [y]$ . L'application h est donc injective.

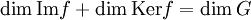D'après le théorème du rang, ${\rm dim \, Im }f+{\rm dim \, Ker }f = \dim G$ ,

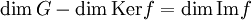alors $\dim G - {\rm dim \, Ker }f = {\rm dim \, Im }f$ .

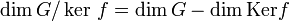Or, $\dim G/\ker \, f = \dim G - {\rm dim \, Ker }f$ .

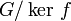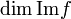Donc, $G/\ker \, f$ et ${\rm dim \, Im }f \,$ ont même dimension.

Comme l'espace de départ et d'arrivée de h ont même dimension, si h est injective, alors h est aussi surjective. Donc h est un isomorphisme.

Ici, $ker f$ désigne le noyau de $f$ et $G / ker f$ désigne le quotient du groupe $G$ par le noyau de $f$ .

On a donc le diagramme commutatif suivant :

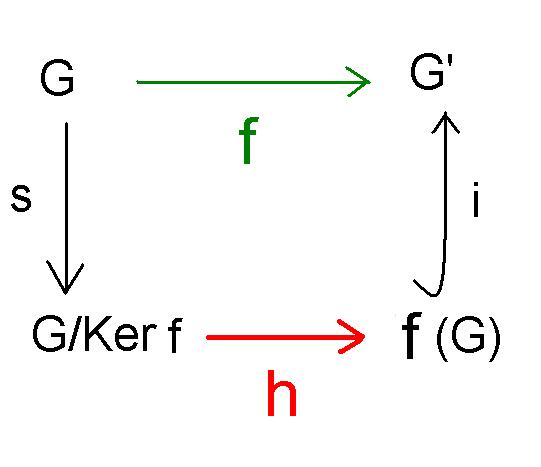
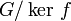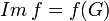où s est la surjection canonique, i l'injection identité et $h$ est l'isomorphisme induit de $G/\ker \, f$ vers $Im \, f = f(G)$ .

Deuxième théorème d'isomorphisme

Deuxième théorème d'isomorphisme — Soient $G$ un groupe, $N$ un sous-groupe normal de $G$ et $H$ un sous-groupe de $G$ . Alors 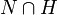$N \cap H$ est un sous-groupe normal de $H$ , et on a l'isomorphisme suivant:

$H/(H\cap N)\simeq N H/N.$

Démonstration

Troisième théorème d'isomorphisme

Troisième théorème d'isomorphisme — Soient $G$ un groupe, $N$ et $M$ deux sous-groupes normaux de $G$ . Alors $N / M$ est alors un sous-groupe normal de $G / M$ et on a l'isomorphisme suivant :

$(G/M)/(N/M)\simeq G/N.$

Démonstration

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8mes d%27isomorphisme ».

Catégories : Théorème de mathématiques | Théorie des groupes

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorèmes d'isomorphismes de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Théorèmes d'isomorphisme — En mathématiques, les trois théorèmes d isomorphisme fournissent l existence d isomorphismes dans le cadre de la théorie des groupes. Ces trois théorèmes d isomorphisme sont généralisables à d autres structures que les groupes. Voir notamment à… … Wikipédia en Français
Homomorphisme De Groupes — Morphisme de groupes Un morphisme de groupes ou homomorphisme de groupes est une application entre deux groupes qui respecte la structure des groupes. Plus précisément, si (G,*) et (G , ) sont deux groupes de neutres respectifs e et e , une… … Wikipédia en Français
Homomorphisme de groupe — Morphisme de groupes Un morphisme de groupes ou homomorphisme de groupes est une application entre deux groupes qui respecte la structure des groupes. Plus précisément, si (G,*) et (G , ) sont deux groupes de neutres respectifs e et e , une… … Wikipédia en Français
Homomorphisme de groupes — Morphisme de groupes Un morphisme de groupes ou homomorphisme de groupes est une application entre deux groupes qui respecte la structure des groupes. Plus précisément, si (G,*) et (G , ) sont deux groupes de neutres respectifs e et e , une… … Wikipédia en Français
Morphisme de groupe — Morphisme de groupes Un morphisme de groupes ou homomorphisme de groupes est une application entre deux groupes qui respecte la structure des groupes. Plus précisément, si (G,*) et (G , ) sont deux groupes de neutres respectifs e et e , une… … Wikipédia en Français
Théorème d'isomorphisme — Théorèmes d isomorphisme En mathématiques, les trois théorèmes d isomorphisme fournissent l existence d isomorphismes dans le cadre de la théorie des groupes. Ces trois théorèmes d isomorphisme sont généralisables à d autres structures que les… … Wikipédia en Français
Emmy Noether — Portrait de Emmy Noether avant 1910. Naissance 23 mars 1882 Erlangen (Bavière, Allemagne) Décès 14 avril … Wikipédia en Français
Groupe classique — En mathématiques, les groupes classiques sont différentes familles de groupes de transformations liées à l algèbre linéaire, principalement les groupes linéaires, orthogonaux, symplectiques et unitaires. Ces groupes peuvent aussi être présentés… … Wikipédia en Français
Morphisme de groupes — Un morphisme de groupes ou homomorphisme de groupes est une application entre deux groupes qui respecte la structure des groupes. Plus précisément, si (G, * ) et sont deux groupes de neutres respectifs e et e , une application est un morphisme du … Wikipédia en Français
GROUPES (mathématiques) - Groupes finis — Née de l’étude des groupes de permutations des racines d’équations, la théorie des groupes finis s’est développée indépendamment depuis le Traité des substitutions et des équations algébriques (1870) de Camille Jordan. Après les travaux… … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Théorèmes d'isomorphismes