- Théorèmes de Carnot
-
Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom.Le terme de théorème de Carnot peut renvoyer à des propositions très différentes et le nom de Carnot ne désigne pas la même personne selon les cas.
On peut citer trois utilisations :
- Le théorème de Carnot en thermodynamique, aussi appelé égalité de Clausius-Carnot que l'on retrouve dans le cycle de Carnot. Dans ce cas, il s'agit de Nicolas Léonard Sadi Carnot, physicien et ingénieur français (1796-1832)[1],[2],[3].
- Le théorème de Carnot de géométrie euclidienne portant sur une égalité algébrique de distances dans une construction faisant appel au cercle inscrit et au cercle circonscrit à un triangle ; que l'on peut aussi retrouver sous le nom de théorème japonais de Carnot. Il s'agit ici de Lazare Nicolas Marguerite Carnot, mathématicien, physicien, général et homme politique français. (1753-1823)[4],[5],[6].
- Le théorème de Carnot de géométrie euclidienne portant sur une courbe algébrique de degré n sécante à un triangle, généralisation d'un théorème de Ménélaos d'Alexandrie. Il s'agit ici encore de Lazare Nicolas Marguerite Carnot[7],[8],[9].
Sommaire
Le « théorème japonais » de Carnot
En 1800, un samouraï anonyme accrochait au mur d'un temple une tablette de bois sur laquelle était gravé un sangaku, problème de géométrie dédié à une divinité (un kami) et proposé à la sagacité des fidèles. En 1803, Lazare Carnot publiait sa Géométrie de position. Hasard de l'Histoire, un théorème de cet ouvrage permet de résoudre élégamment le sangaku précité.
Énoncé
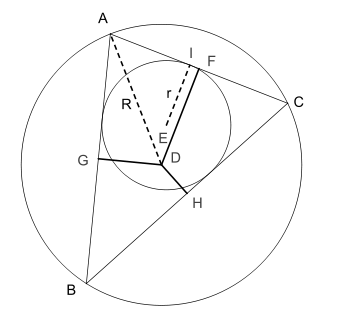
Théorème de Carnot — Soit un triangle ABC et son cercle circonscrit de centre D et de rayon R. La somme des distances "signées" du centre D aux côtés du triangle est donnée par :
où r est le rayon du cercle inscrit au triangle et F, G, H les projetés orthogonaux de D respectivement sur les côtés [AC], [AB] et [BC]
Triangle obtusangle Triangle acutangle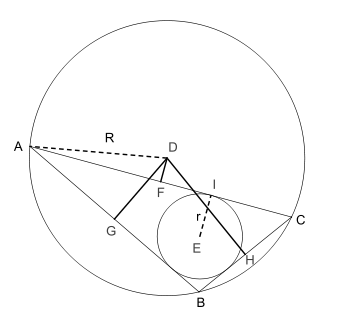 
Théorème de Carnot
Le théorème de Carnot s'énonce ainsi :
Étant donnée une courbe algébrique quelconque de degré n qui coupe un triangle ABC, soit A1 (resp. B1 et C1) le produit des n distances, réelles ou imaginaires, de A (resp. B et C) aux n points d'intersection de la courbe avec le côté AB (resp. BC et CA), et soient de même A2, B2 et C2 les produits semblables associés aux côtés AC, BA et CB. Alors A1B1C1 = A2B2C2.
Références
- B.O. n°16 du 17 avril 2003, Ministère de la jeunesse, de l'éducation nationale et de la recherche.
- X. Bataille, Nicolas Léonard Sadi Carnot, Site de Sciences Physiques et Chimiques de Paris.
- C. Saint Blanquet, Considérations sur les machines thermiques, université de Nantes, 2004
- (en) Eric W. Weisstein, « Carnot's Theorem », MathWorld
- (en) A. Bogomolny, Carnot's Theorem, sur cut-the-knot
- (en) Chris Boucher, "Carnot's Theorem", sur le Wolfram Demonstrations Project
- A. Mannheim, Note à propos d'un théorème connu de géométrie, Bulletin de la SMF, tome 25, p. 78-82, 1897 [PDF]
- Théorème de Carnot par Dominique Tournès, IUFM de La Réunion
- M. Chasles, Traité des sections coniques, faisant suite au traité de géométrie supérieure, Paris, Gauthier-Villars, 1865, sur Google Livres.
Catégories :- Homonymie
- Géométrie du triangle
- Théorème de géométrie
Wikimedia Foundation. 2010.
