- Isomorphisme de Curry-Howard
-
Correspondance de Curry-Howard
La correspondance de Curry-Howard, appelée[1] également correspondance preuve/programme ou correspondance formule/type, est une série de résultats à la frontière entre la logique mathématique, l'informatique théorique et la théorie de la calculabilité établissant une relation entre les démonstrations formelles d'un système logique et les programmes d'un modèle de calcul. Les premiers exemples de correspondance de Curry-Howard remontent à 1958 date à laquelle Curry remarqua l'analogie formelle entre les démonstrations des systèmes à la Hilbert et la logique combinatoire, puis à 1969 où William Alvin Howard remarqua que les démonstrations en déduction naturelle intuitionniste pouvaient formellement se voir comme des termes du lambda-calcul typé.
La correspondance de Curry-Howard a joué un rôle important en logique, car elle a établi un pont entre théorie de la démonstration et informatique théorique. On la retrouve utilisée sous une forme ou une autre dans de très nombreux travaux allant des années 60 à nos jours : sémantique dénotationnelle, logique linéaire, réalisabilité, démonstration automatique...
Sommaire
Historique
La correspondance de Curry-Howard était connue de Curry pour la logique combinatoire dès la fin des années quarante. Howard a publié en 1980[2] un article qui présente formellement la correspondance pour le lambda calcul simplement typé, mais il n'a fait que rendre public un document qui avait déjà circulé dans le monde des logiciens. Elle était connue indépendamment de Lambek pour les catégories cartésiennes fermées, de Girard pour le système F et de de Bruijn pour le système AUTOMATH. Au moins ces cinq noms pourraient être associés à ce concept.
Logique implicative minimale
Par exemple, en lambda calcul simplement typé, si on associe à chaque type de base une variable propositionnelle et que l'on associe l'implication logique
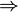au constructeur de type 
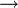alors les propositions démontrables de la logique implicative minimale (où le seul connecteur est l'implication) correspondent aux types des termes clos du lambda calcul.Par exemple, à la proposition
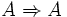on associe le lambda-terme 
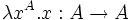.En revanche, il n'y a pas de lambda terme clos associé à la proposition
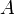ou à la proposition 
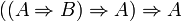(Loi de Peirce), car elles ne peuvent pas être démontrées en logique implicative minimale.Mais la correspondance s'étend aussi aux démontrations et aux normalisations de démonstrations comme suit :
- les types sont les propositions ;
- les termes sont les démonstrations ;
- les réductions des termes sont les normalisations de démonstrations.
Calcul propositionnel
Si on étend le lambda calcul au produit cartésien, on aura parallèlement le et logique. Si on rajoute la somme disjointe (types somme ou structures) on aura le ou logique. Dans les lambda-calculs d'ordre supérieurs on rajoute des variables de types donc des quantificateurs. Cela donne les pour tout.
Calcul du second ordre
Grâce à cette correspondance on peut prouver la cohérence d'une logique en démontrant la normalisation forte du lambda-calcul associé (aucun terme ne se réduit infiniment). C'est ainsi que Jean-Yves Girard a résolu la conjecture de Takeuti, à savoir démontrer la cohérence de l'arithmétique du second ordre ; il l'a fait en établissant la normalisation forte du Système F.
Correspondances
Quelques correspondances entre systèmes fonctionnels et systèmes formels Système fonctionnel Système formel Calcul des constructions (Thierry Coquand) ? Système F (Jean-Yves Girard) Arithmétique de Peano du second ordre / Logique intuitionniste du second ordre Système T (Kurt Gödel) Arithmétique de Peano du premier ordre / Logique intuitionniste du premier ordre Système T1 ? T0 (Récursion primitive) (Stephen Cole Kleene ? Thoralf Skolem ?) Arithmétique primitive récursive Lambda-calcul simplement typé Calcul propositionnel minimal implicatif (déduction naturelle) Logique combinatoire Calcul propositionnel minimal implicatif (à la Hilbert) Calcul lambda-µ de Parigot Déduction naturelle en calcul propositionnel classique Calcul lambda-µ-µ~ de Curien et Herbelin Calcul des séquents classique Calcul symétrique de Berardi et calcul dual de Wadler Calcul des séquents avec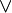 
et 
Logique et informatique
Le logicien français, Jean-Louis Krivine a fait le rapport entre différents théorèmes mathématiques et les programmes informatiques qu'ils représentent.
- l'absurde (appelé « bottom » :
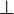) a pour lambda-terme λx.x, ce qui correspond à « pour tout x, x » c’est-à-dire que tout est vrai. Comme on utilise un système cohérent ceci est toujours faux. En informatique, cela correspond à une instruction d'échappement, d'exception. - le théorème d'incomplétude de Gödel qui dit qu'il y a des théorèmes que l'on ne peut pas démontrer correspond à un programme de réparation de fichiers.
- le théorème de complétude de Gödel correspond lui à un désassembleur interactif de programmes[3].
Références
Le livre de référence est le livre de Girard- Lafont-Taylor connu sous le nom de Girafon.
- ↑ La terminologie isomorphime de Curry-Howard tombé en désuétude.
- ↑ Howard, W., The formulas--as--types notion of construction, in Essays on Combinatory Logic, Lambda Calculus, and Formalism, Seldin, J. P. and Hindley, J. R. ed., Academic Press (1980) pp. 479--490,
- ↑ Jean-Louis Krivine, Une preuve formelle et intuitionniste du théorème de complétude de la logique classique, Bull. Symb. Log. 2, 4, p. 405-421 (1996). Voir en ligne.
Portail de la logique
Portail de l’informatique
Catégories : Calculabilité | Logique mathématique | Théorie de la démonstration | Théorie des types
Wikimedia Foundation. 2010.
