Théorème de morley

Théorème de Morley

Le théorème de Morley, découvert par Frank Morley en 1898, est un théorème de géométrie plane. Il s'énonce comme suit :
« Les intersections des trissectrices des angles d'un triangle forment un triangle équilatéral »

Le triangle équilatéral ainsi défini par le théorème de Morley s'appelle le « triangle de Morley » du triangle de départ.

Sommaire

1 Démonstrations
- 1.1 Première démonstration
- 1.2 Deuxième démonstration
2 Triangle de Morley
- 2.1 Longueur des côtés
- 2.2 Orientation du triangle de Morley
3 Liens externes

Démonstrations

Première démonstration

démonstration du théorème

Cette méthode simple utilise les lois trigonométriques.

On peut en effet déterminer, d'après la loi des sinus, la longueur de la plupart des segments à partir des côtés du triangle. Par ailleurs, le Théorème d'Al-Kashi nous permet de déterminer et de comparer les autres, notamment QR, PR, et PQ - les trois côtés du triangle rouge, celui qui est censé être équilatéral.

On définit les angles a, b et c tels que :

$\widehat {BAC} = 3 \times a$
$\widehat {ABC} = 3 \times b$
$\widehat {ACB} = 3 \times c$

Puisque dans tout triangle on a :

$\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ$

notre changement de variable ci-dessus donne :

$a + b + c = 60^\circ$ .

De plus, pour simplifier les calculs on adopte une unité telle que le rayon du cercle circonscrit au triangle est 1. On a alors :

AB = 2 sin(3c)
BC = 2 sin(3a)
AC = 2 sin(3b).

Dans le triangle BPC, d'après la loi des sinus, on a :

$\frac {BP}{\sin (c)} = \frac {BC}{\sin (180^\circ - b - c)} = \frac {2 \sin (3a)}{\sin (b + c)} = \frac {2 \sin (3a)}{\sin (60^\circ - a)}$

$BP = \frac {2 \sin (3a) \sin (c)}{\sin (60^\circ - a)}$

On peut développer sin(3a) :

sin(3a) = 3sin(a) - 4sin3(a)
3sin(a) - 4sin3(a) = 4sin(a)[(√3/2)² - sin²(a)]
4sin(a)[(3/2)² - sin²(a)] = 4sin(a)[sin²(60°) - sin²(a)]
4sin(a)[sin²(60°) - sin²(a)] = 4sin(a)[sin(60°) + sin(a)][sin(60°) - sin(a)]
4sin(a)[sin(60°) + sin(a)][sin(60°) - sin(a)] = 4sin(a) 2sin[(60°) + a)/2]cos[(60°) - a)/2] × 2sin[(60°) - a)/2]cos[(60°) + a)/2]
sin(a) 2sin[(60°) + a)/2]cos[(60°) - a)/2] × 2sin[(60°) - a)/2]cos[(60°) + a)/2] = 4sin(a)sin(60° + a)sin(60° - a)

Ce qui nous permet de simplifier l'expression de BP :

$BP = 8 \sin(a) \sin(c) \sin(60^\circ + a)$

Mais que l'on peut appliquer également à BR :

$BR = 8 \sin(a) \sin(c) \sin(60^\circ + c)$

Al-Kashi nous donne : PR² = BP² + BR² - 2BPBR cos(b). Si on développe, on obtient :

$PR^2 = 64 \sin^2 (a) \sin^2 (c)[ \sin^2(60^\circ + a) + \sin^2 (60^\circ + c) - 2 \sin(60^\circ + a) \sin (60^\circ + c) \cos(b)]$

Or, (60° + a) + (60° + c) + b = 120° + (a + b + c) = 120° + 60° = 180 °. Parmi les triangles ayant pour angle 60° + a, 60° + c et b dont le rayon du cercle circonscrit est 1, si on applique Al-Kashi, on a :

sin²(b) = sin²(60° + a) + sin²(60° + c) - 2 sin(60° + a) sin(60° + c) cos(b)

PR = 8 sin(a) sin(b) sin(c)

PQ = 8 sin(b) sin(a) sin(c)

QR = 8 sin(a) sin(c) sin(b)

PR = PQ = QR

Le triangle PQR est donc bien équilatéral.

Deuxième démonstration

Cette démonstration est basée sur un article d'Alain Connes. Elle utilise les nombres complexes et donne un calcul rapide de l'affixe des sommets du triangle équilatéral.

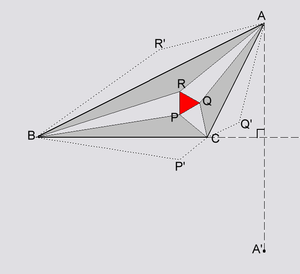
Plaçons-nous dans le plan euclidien orienté que nous pourrons ultérieurement identifier au corps des complexes. Désignons par P, Q et R les 3 intersections de trisectrices dont on veut montrer qu'elles forment un triangle équilatéral. En outre plaçons les points P', Q' et R' symétriques de P, Q et R respectivement par rapport à BC, CA, AB (voir figure ci-contre). Désignons enfin respectivement par $\quad \alpha,\beta,\gamma$ la détermination principale (comprise entre $\quad -\pi$ et $\quad \pi$ ) des angles $\widehat {(\overrightarrow {AB},\overrightarrow {AC})},\;\widehat{(\overrightarrow {BC},\overrightarrow {BA})},\;\widehat{(\overrightarrow {CA},\overrightarrow {CB})}$ .

Soient maintenant $\; f, g, h \quad$ les rotations de centres respectifs A, B, C et d'angles respectifs $2\alpha/3,\;2\beta/3,\;2\gamma/3$ .

(i) P (resp. Q, R) est le point fixe de $g\circ h$ (resp. $h\circ f ,\; f \circ g$ ).
En effet $h$ transforme P en P' et $g$ transforme P' en P (immédiat: voir figure). Il en est de manière analogue pour Q et R.
(ii) $f^3 \circ g^3 \circ h^3 = Id$ (application identique).
En effet la somme des angles des rotations composantes est $2π$ et on obtient donc une translation. Mais A est invariant puisque $h 3$ (rotation de centre C et d'angle $2γ$ ) transforme A en A' symétrique de A par rapport à BC, $g 3$ transforme A' en A et finalement $f 3$ laisse A invariant. Par suite cette translation est l'application identique.

Il est tout à fait remarquable que les seules propositions (i) et (ii) ci-dessus sont suffisantes pour en déduire le caractère équilatéral du triangle PQR. Il n'est même pas besoin de supposer que $f,\,g\,\,h$ sont des rotations mais seulement que ce sont des applications affines du corps des complexes (identifié au plan) avec la seule restriction toutefois que ni $f \circ g$ ni $g \circ h$ ni $h \circ f$ ni $f \circ g \circ h$ ne sont des translations.

Ainsi, nous allons désormais travailler dans le corps des complexes en conservant les notations que nous avons introduites.

Nous définissons simplement $f,\,g,\,h$ (applications affines) par

$\quad f(x)=a_1.x+b_1$

$\quad g(x)=a_2.x+b_2$

$\quad h(x)=a_3.x+b_3 \qquad (a_1a_2, \;a_2a_3, \;a_3a_1 , \;a_1a_2a_3$ différents de 1).

Un calcul rapide montre que (i) équivaut à

$\quad P=(a_2b_3+b_2)/(1-a_2a_3)$

$\quad Q=(a_3b_1+b_3)/(1-a_3a_1)$

$\quad R=(a_1b_2+b_1)/(1-a_1a_2)$

Quant à (ii) on montre aisément l'équivalence avec

$\quad (a_1a_2a_3)^3=1$

$\quad (a_1^2+a_1+1)b_1+a_1^3(a_2^2+a_2+1)b_2+a_1^3a_2^3(a_3^2+a_3+1)b_3=0$

Comme $a_1a_2a_3 \ne 1$ , on voit que $\quad a_1a_2a_3 = j$ ou $\quad j^2$ . Supposons pour fixer les idées que $\quad a_1a_2a_3 = j$ (cela correspondra dans l'application à un triangle ABC de sens positif).

Maintenant, après 2 lignes de calcul, on obtient :

$\quad P+jQ+j^2R=[(1-a_2a_3)a_3(j^2-a_1)b_1+(1-a_3a_1)a_1(1-a_2j)b_2+(1-a_1a_2)a_2(j-a_3j^2)b_3]/[(1-a_1a_2)(1-a_2a_3)(1-a_3a_1)]$

$\quad =[a_3/a_1(a_1^2+a_1+1)+a_1/a_2j(a_2^2+a_2+1)+a_2/a_2j^2(a_3^2+a_3+1)]/[(1-a_1a_2)(1-a_2a_3)(1-a_3a_1)]$

$\quad =-a_3/a_1[(a_1^2+a_1+1)b_1+a_1^3(a_2^2+a_2+1)b_2+a_1^3a_2^3(a_3^2+a_3+1)b_3]/[(1-a_1a_2)(1-a_2a_3)(1-a_3a_1)]$

Démonstration détaillée de l'égalité ci-dessus

Sachant que

$\quad b = (a_1^2+a_1+1)b_1+a_1^3(a_2^2+a_2+1)b_2+(a_1a_2)^3(a_3^2+a_3+1)b_3$

$\quad j = a_1a_2a_3$

$\quad j^3 = 1$

on montre que $\quad b=-ja_1^2a_2(a_1-j)(a_2-j)(a_3-j)(P+jQ+j^2R)$ .

On a

$P+jQ+j^2R=\frac{(a_1b_2+b_1)(1-a_2a_3)(1-a_3a_1)}{(1-a_1a_2)(1-a_2a_3)(1-a_3a_1)}+ \frac{j(a_2b_3+b_2)(1-a_1a_2)(1-a_3a_1)}{(1-a_1a_2)(1-a_2a_3)(1-a_3a_1)}+$

$\quad\frac{j^2(a_3b_1+b_3)(1-a_1a_2)(1-a_2a_3)}{(1-a_1a_2)(1-a_2a_3)(1-a_3a_1)}$

$=\frac{a_1b_2(1-a_2a_3)(1-a_3a_1)+ jb_2(1-a_1a_2)(1-a_3a_1)}{(1-a_1a_2)(1-a_2a_3)(1-a_3a_1)}+$

$\frac{b_1(1-a_2a_3)(1-a_3a_1) + j^2a_3b_1(1-a_1a_2)(1-a_2a_3)}{(1-a_1a_2)(1-a_2a_3)(1-a_3a_1)}+$

$\frac{ja_2b_3(1-a_1a_2)(1-a_3a_1) + j^2b_3(1-a_1a_2)(1-a_2a_3)}{(1-a_1a_2)(1-a_2a_3)(1-a_3a_1)}$

$=\frac{(1-a_2a_3)b_1a_3(j^2-j^2a_1a_2-a_1+a_1^3a_2^3a_3^2)}{(1-a_1a_2)(1-a_2a_3)(1-a_3a_1)}+$

$\frac{(1-a_3a_1)b_2a_1(1-a_2a_3+ja_1^2a_2^3a_3^3-ja_2)}{(1-a_1a_2)(1-a_2a_3)(1-a_3a_1)}+$

$\frac{(1-a_1a_2)b_3a_2(j-ja_3a_1+j^2a_1^3a_2^3a_3^2-j^2a_3)}{(1-a_1a_2)(1-a_2a_3)(1-a_3a_1)}$

$=\frac{(1-a_2a_3)b_1a_3(j^2-a_1)+ (1-a_3a_1)b_2a_1(1-ja_2)+ (1-a_1a_2)b_3a_2(j-j^2a_3)}{(1-a_1a_2)(1-a_2a_3)(1-a_3a_1)}$

Puis on multiplie par le dénominateur et par $j^2a_1^2a_2$ des deux côtés:

$(P+jQ+j^2R)(1-a_1a_2)(1-a_2a_3)(1-a_3a_1)j^2a_1^2a_2 =$

$j^2a_1^2a_2[(1-a_2a_3)b_1a_3(j^2-a_1)+(1-a_3a_1)b_2a_1(1-ja_2)+(1-a_1a_2)b_3a_2(j-j^2a_3)]$

$=a_1b_1(1-a_2a_3)(j^2-a_1)+a_1^3b_2j^2(a_2-j)(1-ja_2)+a_1^2a_2^2b_3(1-a_1a_2)(1-ja_3)$

$=b_1(a_1-j)(j^2-a_1)+a_1^3b_2(a_2-j)(j^2-a_2)+(a_1a_2)^3b_3((a_1a_2)^2a_3^3-1)(1-ja_3)$

$=b_1(a_1j^2-a_1^2-j^3+a_1j)+a_1^3b_2(a_2j^2-a_2^2-j^3+ja_2)+(a_1a_2)^3b_3((a_1a_2)^2a_3^3-j(a_1a_2)^2a_3^3a_3-1+ja_3)$

$=b_1(a_1(j^2+j)-a_1^2-1)+a_1^3b_2(a_2(j^2+j)-a_2^2-1)+(a_1a_2)^3b_3(a_3(j^2+j)-a_3^2-1)$

Puisque $j^3=1\quad \Rightarrow j^2+j+1=0 \Rightarrow j^2+j=-1$ et ainsi

$-ja_1^2a_2(a_1-j)(a_2-j)(a_3-j)(P+jQ+j^2R) =$

$b_1(a_1^2+a_1+1)+a_1^3b_2(a_2^2+a_2+1)+(a_1a_2)^3b_3(a_3^2+a_3+1)=b$

Et donc $\quad P+jQ+j^2R=0.$ Ceci montre bien que le triangle PQR est équilatéral (de sens positif) (caractérisation classique).

Naturellement si le triangle ABC est de sens négatif, on devra prendre $\quad a_1a_2a_3=j^2$ et on obtient PQR équilatéral de sens négatif.

Dans le cas où ABC est de sens positif, on a en fait

$\quad f(z)=e^{2i \alpha /3}(z-A)+A \qquad g(z)=e^{2i \beta /3}(z-B)+B \qquad h(z)=e^{2i \gamma /3}(z-C)+C$

et donc $\quad a_1=e^{2i \alpha /3} \quad b_1=(1-e^{2i \alpha /3})A$ et expressions analogues pour $\quad a_2,b_2,a_3,b_3$ . Il est donc très aisé de déterminer P, Q et R.

Triangle de Morley

Longueur des côtés

Chaque côté du triangle de Morley mesure :

8R sin A/3.sin B/3.sin C/3,

où R désigne le rayon du cercle circonscrit au triangle de départ.

Orientation du triangle de Morley

Orientation par rapport au triangle de départ : le côté B'C' du triangle de Morley situé le plus près du sommet A fait avec le côté BC du triangle de départ un angle égal à (C-B)/3, où C et B désignent les angles BCA et ABC.
Orientation par rapport à la deltoïde de Steiner : le triangle (équilatéral) formé par les points de rebroussement de la deltoïde de Steiner et le triangle (équilatéral) de Morley, ont leurs côtés parallèles.

Liens externes

Voir les 27 triangles équilatéraux formés par les trissectrices

Portail de la géométrie

Ce document provient de « Th%C3%A9or%C3%A8me de Morley ».

Catégories : Théorème de géométrie | Géométrie du triangle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de morley de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Théorème de Morley — En mathématiques, et plus précisément en géométrie plane, le théorème de Morley, découvert par Frank Morley (en) en 1898, affirme que : « Les intersections des trissectrices des angles d un triangle forment un triangle… … Wikipédia en Français
Theoreme de Morley — Théorème de Morley Le théorème de Morley, découvert par Frank Morley en 1898, est un théorème de géométrie plane. Il s énonce comme suit : « Les intersections des trissectrices des angles d un triangle forment un triangle… … Wikipédia en Français
Morley (homonymie) — Morley Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Morley désigne : Sommaire 1 Nom de famille 2 Littérature … Wikipédia en Français
Morley — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Morley désigne : Sommaire 1 Nom de famille 2 Littérature … Wikipédia en Français
MODÈLES (THÉORIE DES) — «Modèle» est un terme qui appartient au vocabulaire de la plupart des sciences et qui a des significations multiples [cf. MODÈLE]. Ainsi, dans les sciences humaines, on entend généralement par modèle une théorie conçue pour expliquer un ensemble… … Encyclopédie Universelle
Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… … Wikipédia en Français
Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Théorie k-catégorique — En logique mathématique, une théorie est dite k catégorique pour un nombre cardinal k si elle a exactement un modèle de cardinalité k (à isomorphisme près). Sommaire 1 Théorème de Łoś Vaught 1.1 Énoncé 1.2 … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de morley