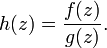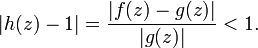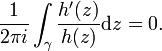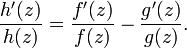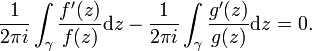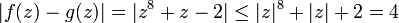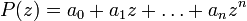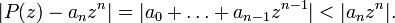Théorème de rouché

Théorème de Rouché

En analyse complexe, le théorème de Rouché est un énoncé important sur les zéros et les pôles des fonctions méromorphes. Il est nommé ainsi en l'honneur du mathématicien français Eugène Rouché.

Sommaire

1 Enoncé du théorème
2 Démonstration
3 Exemple
4 Applications
- 4.1 Démonstration du théorème fondamental de l'algèbre
5 Voir Aussi
6 Références

Enoncé du théorème

Soit 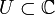$U \subset \mathbb C$ un ouvert simplement connexe, soit $f$ et $g$ deux fonctions méromorphes sur $U$ avec un ensemble fini $F$ de zéros et de pôles. Soit $γ$ un lacet simple positivement orienté à image dans $U - F$ formant le bord 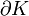$\partial K$ d'un compact $K$ , si pour tout 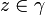$z \in \gamma$ on a

| f (z) - g (z) | < | g (z) |

alors

Z f, K - P f, K = Z g, K - P g, K

où $Z f, K$ et $P f, K$ sont respectivement le nombre de zéros et de pôles de $f$ (en tenant compte de leur mutliplicité) contenus dans $K$ .

Démonstration

Si $| f (z) - g (z) | < | g (z) |$ pour tout 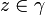$z\in \gamma$ , alors $f$ et $g$ sont non nulles sur $γ$ (sinon l'inégalité stricte ne pourrait pas être vérifiée). Soit $h$ la fonction méromorphe sur $U$ , holomorphe et non nulle sur $γ$ définie par :

$h(z) = \frac{f(z)}{ g(z)}.$

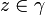
On a pour tout $z \in \gamma$

$|h(z) - 1| = \frac{|f(z)-g(z)|}{|g(z)|} < 1.$

L'image de $γ$ par $h$ est donc contenue dans le disque ouvert de rayon 1 et de centre 1 $D (1,1)$ et par conséquent elle ne tourne pas autour de l'origine. En appliquant le principe de l'argument on a donc :

$\frac{1}{2\pi i} \int_\gamma \frac{h'(z)}{h(z)} \mathrm{d}z = 0.$

D'autre part, on a

$\frac{h'(z)}{h(z)} = \frac{f'(z)}{f(z)} - \frac{g'(z)}{g(z)}.$

Par conséquent,

$\frac{1}{2\pi i} \int_\gamma \frac{f'(z)}{ f(z)} \mathrm{d}z - \frac{1}{ 2\pi i} \int_\gamma \frac{g'(z)}{g(z)} \mathrm{d}z = 0.$

Finalement, en utilisant à nouveau le principe de l'argument, on obttient

Z f, K - P f, K = Z g, K - P g, K .

Exemple

Considérons les deux fonctions $f$ et $g$ définies comme suit :

f (z) = z 8 - 5 z 3 + z - 2

g (z) = - 5 z 3

et considérons pour lacet le cercle positivement orienté 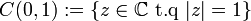$C(0, 1) := \{z\in\mathbb C\, \, \mathrm{t.q}\,\, |z|=1 \}$ . On vérifie sur ce lacet que :

$|f(z) - g(z)| = |z^8+z-2| \le |z|^8+|z|+2 = 4$

| g (z) | = | - 5 z 3 | = 5.

On peut donc appliquer le théorème de Rouché :

Z f = Z g

puisque $f$ et $g$ n'ont pas de pôle. Par ailleurs, $g$ a un zéro triple à l'origine ce qui nous indique donc que la fonction $f$ admet trois zéros dans le disque ouvert $D (0,1)$ .

Applications

Démonstration du théorème fondamental de l'algèbre

Article détaillé : Théorème de d'Alembert-Gauss.

Soit un polynôme $P$ à valeurs dans $\mathbb C$ et défini par :

$P(z) = a_0 + a_1z + \dots + a_nz^n$

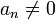en supposant $a_n \neq 0$ . Soit $R > 0$ suffisamment grand pour que pour tout 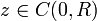$z \in C(0, R)$ on vérifie :

$|P(z) - a_nz^n| = |a_0+\dots+a_{n-1}z^{n-1}| < |a_nz^n|.$

Etant donné que $a n z n$ admet un zéro d'ordre $n$ à l'origine, $P$ doit admettre $n$ zéros dans le disque ouvert $D (0, R)$ par application du théorème de Rouché.

Voir Aussi

Références

Michèle AUDIN, Analyse Complexe, notes de cours de l'université de Strasbourg disponibles en ligne.
Murray R. SPIEGEL, Variables Complexes, Schaum, ISBN 2-7042-0020-3

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de Rouch%C3%A9 ».

Catégories : Analyse complexe | Théorème de mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de rouché de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Theoreme de Rouche — Théorème de Rouché En analyse complexe, le théorème de Rouché est un énoncé important sur les zéros et les pôles des fonctions méromorphes. Il est nommé ainsi en l honneur du mathématicien français Eugène Rouché. Sommaire 1 Enoncé du théorème 2… … Wikipédia en Français
Théorème de Rouché — Ne doit pas être confondu avec le théorème de Rouché Fontené (en) en algèbre linéaire. En analyse complexe, le théorème de Rouché est un énoncé important sur les zéros et les pôles des fonctions méromo … Wikipédia en Français
Théorème de d'Alembert — Gauss Pour les articles homonymes, voir Théorème de Gauss. Jean le Rond D Alembert est le premier à ressentir la nécessité de démontrer le th … Wikipédia en Français
Théorème de d’Alembert-Gauss — Théorème de d Alembert Gauss Pour les articles homonymes, voir Théorème de Gauss. Jean le Rond D Alembert est le premier à ressentir la nécessité de démontrer le th … Wikipédia en Français
Théorème fondamental de l'algèbre — Théorème de d Alembert Gauss Pour les articles homonymes, voir Théorème de Gauss. Jean le Rond D Alembert est le premier à ressentir la nécessité de démontrer le th … Wikipédia en Français
Théorème de d'Alembert-Gauss — Pour les articles homonymes, voir Théorème de Gauss. Jean le Rond D Alembert est le premier à ressentir la nécessité de démontrer le théorème fondamental de l algèbre. Sa motivation est entièrement analytique, il r … Wikipédia en Français
Théorème de l'application ouverte (analyse complexe) — Ne pas confondre ce théorème ci de l application ouverte avec cet autre : théorème de Banach Schauder. En mathématiques, et plus précisément en analyse complexe, le théorème de l application ouverte affirme que les fonctions… … Wikipédia en Français
Théorème de Lagrange sur les polynômes — Pour les articles homonymes, voir Théorème de Lagrange. Il s agit d un résultat trouvé par le mathématicien Joseph Louis Lagrange[réf. souhaitée] concernant les polynômes. Soit P un polynôme tel que: où les … Wikipédia en Français
Theoreme de Thales — Théorème de Thalès Pour l’article homonyme, voir Théorème de Thalès (cercle). Configuration possible du théorème Le théorème de Thalès ou théorè … Wikipédia en Français
Théorème de Thales — Théorème de Thalès Pour l’article homonyme, voir Théorème de Thalès (cercle). Configuration possible du théorème Le théorème de Thalès ou théorè … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de rouché