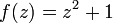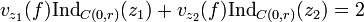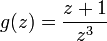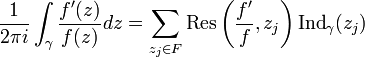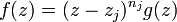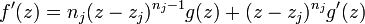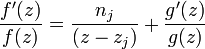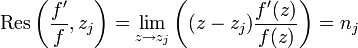- Principe de l'Argument
-
Principe de l'argument
En analyse complexe, le principe de l'argument (parfois appelé Théorème de l'argument[1]) indique que si f est une fonction méromorphe sur un ouvert
 simplement connexe dont l'ensemble F des zéros et des pôles est fini, alors pour tout lacet γ à image dans U\F,
simplement connexe dont l'ensemble F des zéros et des pôles est fini, alors pour tout lacet γ à image dans U\F,
Avec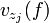 la valuation de f en zj c'est à dire l'ordre du zj si zj est un zéro et moins l'ordre de zj si c'est un pôle. Indγ(zj) est l'indice du point par rapport au lacet.
la valuation de f en zj c'est à dire l'ordre du zj si zj est un zéro et moins l'ordre de zj si c'est un pôle. Indγ(zj) est l'indice du point par rapport au lacet.Si γ est un lacet simple positivement orienté formant le bord
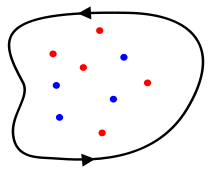
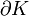 d'un compact K, la relation ci-dessus se réécrit :
d'un compact K, la relation ci-dessus se réécrit :où Zf,K et Pf,K représentent respectivement le nombre de zéros et de pôles de f dans K comptés avec leur multiplicité.
Sommaire
Interprétation géométrique
Le principe de l'argument permet de compter le nombre de tour que fait l'image de γ par f autour de l'origine. C'est sur cette notion que se base notamment la démonstration du Théorème de Rouché.
Exemples
Soit la fonction
 ayant deux zéros simples en
ayant deux zéros simples en 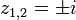 (la valuation de ces deux points est +1) et définie par :
(la valuation de ces deux points est +1) et définie par :Considérons le lacet le plus simple : le cercle C(0,r) centré à l'origine et de rayon
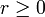 , il y a deux cas à considérer :
, il y a deux cas à considérer :- Tout d'abord si r < 1, alors l'indice des deux zéros est nul et l'image du lacet par f ne tourne pas autour de l'origine.
- L'autre cas est :
 , alors l'indice des deux zéros est égal à 1 et l'image du lacet par f tourne deux fois autour de l'origine en effet :
, alors l'indice des deux zéros est égal à 1 et l'image du lacet par f tourne deux fois autour de l'origine en effet :
Considérons à présent la fonction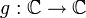 ayant un pôle triple à l'origine et un zéro simple en z2 = − 1 (la valuation de ces deux points est respectivement -3 et +1) et définie par :
ayant un pôle triple à l'origine et un zéro simple en z2 = − 1 (la valuation de ces deux points est respectivement -3 et +1) et définie par :En considérant comme ci-dessus le cercle C(0,r), nous avons à nouveau deux cas à considérer :
- Si r < 1, alors l'indice du zéro simple est nul, et il ne reste que le pôle triple à considérer, l'image du lacet par la fonction g tourne -trois fois (trois fois dans le sens anti-trigonométrique) autour de l'origine.
- Si
 , on doit considérer le zéro et le pôle et donc l'image du lacet par la fonction g tourne -deux fois autour de l'origine.
, on doit considérer le zéro et le pôle et donc l'image du lacet par la fonction g tourne -deux fois autour de l'origine.
Ces deux cas sont illustrés par les figures 1 et 2 ci-contre.
Preuve
Par hypothèse,
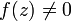 et f est holomorphe sur U\F et donc la
et f est holomorphe sur U\F et donc la 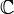 -dérivée f' l'est aussi. Par conséquent, nous pouvons en déduire que f'/f est aussi holomorphe sur U\F.
-dérivée f' l'est aussi. Par conséquent, nous pouvons en déduire que f'/f est aussi holomorphe sur U\F.U est simplement connexe donc le lacet γ est homotope à un point dans U, on peut donc appliquer le Théorème des résidus :
Pour
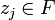 , on a, au voisinage de zj :
, on a, au voisinage de zj :avec g(z) holomorphe et non nulle sur un voisinage de zj et
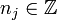 qui correspond à la valuation de zj.
qui correspond à la valuation de zj.On a donc :
dont on tire :
Le quotient ci-dessus a un pôle simple en zj puisque g est holomorphe et non nulle au voisinage de zj. On peut maintenant calculer le résidu en zj :
Avec
 . En insérant ce dernier résultat dans la première équation, nous obtenons finalement :
. En insérant ce dernier résultat dans la première équation, nous obtenons finalement :Applications
Des ouvrages d'Automatique utilisent assez fréquemment ce principe comme base théorique pour le critère de stabilité de Nyquist. La thèse originale de 1932 de Harry Nyquist[2] fait usage d'une approche plutôt maladroite et primitive pour développer le critère de stabilité. Dans sa thése, H. Nyquist ne mentionnait pas le principe de l'argument. Par après, Leroy MacColl[3] et Hendrik Bode[4] sont partis du principe de l'argument pour déterminer le critère de stabilité, approche qui est utilisée actuellement dans bon nombre d'ouvrage d'analyse complexe ou d'automatique
Références
Voir Aussi
- Portail des mathématiques
Catégories : Analyse complexe | Théorème de mathématiques
Wikimedia Foundation. 2010.

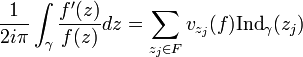
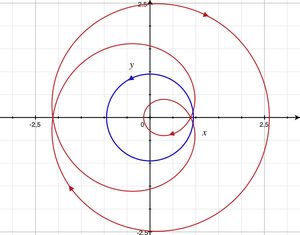
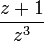 . En bleu le lacet
. En bleu le lacet