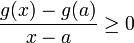Théorème de darboux (analyse)

Théorème de Darboux (analyse)

En mathématiques, et plus particulièrement en analyse, le théorème de Darboux est un théorème nommé en l'honneur du mathématicien Gaston Darboux qui stipule que les fonctions dérivées de fonctions numériques à valeurs réelles vérifient la propriété des valeurs intermédiaires.

Historique

Au XIX^e siècle, la plupart des mathématiciens pensaient que le théorème des valeurs intermédiaires caractérisait les fonctions continues. En 1875, Gaston Darboux mit un terme à cette conviction en montrant que les fonctions dérivées vérifiaient également ce théorème, et en donnant des exemples de fonctions dont la dérivée n'était pas continue. Une telle fonction est

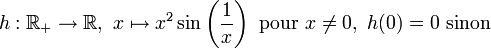$h:\R_+ \rightarrow \R,\ x \mapsto x^2 \sin\left(\frac{1}{x}\right) \text{ pour }x \neq 0,\ h(0)=0 \text{ sinon}$ .

Énoncé

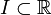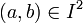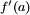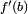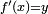Soit $f$ une fonction dérivable sur un intervalle $I \subset \R$ , non vide et non réduit à un point, à valeurs réelles, et soit $(a,b) \in I^2$ tel que $a < b$ . Alors pour tout $y$ strictement compris entre $\scriptstyle f'(a)$ et $\scriptstyle f'(b)$ , il existe $x \in ]a,b[$ tel que $\scriptstyle f'(x)=y$ .

Autre énoncé : Soit 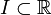$I \subset \R$ , non vide et non réduit à un point, et soit f une application définie sur $I$ à valeurs réelles. Si $f$ est dérivable sur $I$ alors 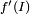$\scriptstyle f'(I)$ est un intervalle.

Démonstration

En reprenant les notations de l'énoncé : considérons la fonction $g:[a,b] \rightarrow \R$ définie par

$\forall x \in [a,b],\ g(x) = f(x) - xy$

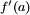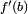où $y$ est un réel strictement compris entre $\scriptstyle f'(a)$ et $\scriptstyle f'(b)$ .

La fonction $g$ est dérivable sur l'intervalle $[a, b]$ et

$\forall x \in [a,b],\ g'(x) = f'(x) - y$

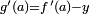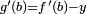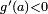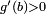En particulier, $\scriptstyle g'(a) = f'(a) - y$ et $\scriptstyle g'(b) = f'(b) - y$ , donc $\scriptstyle g'(a) <0$ et $\scriptstyle g'(b) >0$ par définition de $y$ .

La fonction $g$ étant dérivable sur $[a, b]$ , elle y est continue, et donc elle y admet un minimum.

La fonction $g$ ne peut avoir un minimum en $a$ , car sinon, on aurait, pour $x \in ]a,b]$ :

$\frac{g(x)-g(a)}{x-a} \ge 0$

et en prenant la limite de ce rapport quand $x$ tend vers $a$ , on aurait 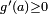$\scriptstyle g'(a) \geq 0$ , ce qui est impossible.

De même, on montre que $g$ ne peut avoir un minimum en $b$ .

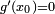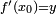Il en résulte que ce minimum est atteint en un point $x_0 \in ]a,b[$ . On a alors $\scriptstyle g'(x_0)=0$ , d'où $\scriptstyle f'(x_0)=y$ .

Applications

Par exemple, on peut montrer que la fonction partie entière n'admet pas de primitive sur $\R$ grâce au théorème de Darboux.

Bibiographie

G. Darboux, Mémoire sur les fonctions discontinues, Ann. Sci. Scuola. Norm. Sup. 4 (1875) 57-112

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de Darboux (analyse) ».

Catégories : Analyse réelle | Théorème de mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de darboux (analyse) de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Theoreme de Darboux (analyse) — Théorème de Darboux (analyse) En mathématiques, et plus particulièrement en analyse, le théorème de Darboux est un théorème nommé en l honneur du mathématicien Gaston Darboux qui stipule que les fonctions dérivées de fonctions numériques à… … Wikipédia en Français
Théorème de Darboux (analyse) — Pour l’article homonyme, voir Théorème de Darboux (géométrie). En mathématiques, et plus particulièrement en analyse, le théorème de Darboux est un théorème nommé en l honneur du mathématicien Gaston Darboux qui stipule que les… … Wikipédia en Français
Theoreme de Darboux — Théorème de Darboux Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Théorème de Darboux (analyse) Théorème de Darboux (géométrie) Ce document provient de « Th%C3%A9or%C3%A8me de Darboux ». Catégorie :… … Wikipédia en Français
Théorème de darboux — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Théorème de Darboux (analyse) Théorème de Darboux (géométrie) Ce document provient de « Th%C3%A9or%C3%A8me de Darboux ». Catégorie : Homonymie … Wikipédia en Français
Théorème de Darboux (géométrie) — Pour l’article homonyme, voir Théorème de Darboux (analyse). Le théorème de Darboux est un théorème central de la géométrie symplectique : les variétés symplectiques de dimension 2n sont deux à deux localement symplectomorphes.… … Wikipédia en Français
Théorème de Darboux — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le théorème de Darboux (analyse) Le théorème de Darboux (géométrie) Voir aussi Gaston Darboux, un mathématicien français (1842 1917). Catégorie :… … Wikipédia en Français
Theoreme des valeurs intermediaires — Théorème des valeurs intermédiaires Pour les articles homonymes, voir TVI. Le théorème des valeurs intermédiaires (TVI) est un théorème important en analyse et concerne des fonctions continues sur un intervalle. Il indique que si une fonction… … Wikipédia en Français
Théorème de Bolzano — Théorème des valeurs intermédiaires Pour les articles homonymes, voir TVI. Le théorème des valeurs intermédiaires (TVI) est un théorème important en analyse et concerne des fonctions continues sur un intervalle. Il indique que si une fonction… … Wikipédia en Français
Theoreme de Stokes — Théorème de Stokes Pour les articles homonymes, voir Stokes. Articles d analyse vectorielle … Wikipédia en Français
Théorème de stokes — Pour les articles homonymes, voir Stokes. Articles d analyse vectorielle … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de darboux (analyse)