Théorème de cayley

Théorème de cayley

Théorème de Cayley

En théorie des groupes, le théorème de Cayley est un résultat élémentaire affirmant que tout groupe se réalise comme sous-groupe d'un groupe de permutations :

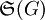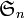Théorème — Tout groupe G est isomorphe à un sous-groupe du groupe symétrique \mathfrak{S}(G) des permutations de G. En particulier, si G est un groupe d'ordre n, il est isomorphe à un sous groupe fini de \mathfrak{S}_n.

Ce théorème fut démontré en 1854 dans un article intitulé Sur la théorie des groupes comme dépendance de l'équation symbolique θn = 1.

Remarques

A noter qu'il plonge un groupe de cardinal fini n, dans un autre groupe de cardinal n!.

Ce théorème est utilisé pour la théorie de représentation des groupes. Soit G un groupe fini de cardinal n et (e1,...,en) une base d'un espace vectoriel E de dimension n. Le théorème de Caley indique que G est isomorphe à un groupe de permutation des éléments de la base. Chaque permutation peut être prolongée en un endomorphisme qui ici par définition est un automorphisme. Cela définit une représentation du groupe, on parle alors de représentation régulière.

Démonstration

Soit G un groupe et g un élément du groupe. On définit l'application tg de G dans G comme étant la translation à gauche :

\forall x\in G\, t_g(x)=gx

Les propriétés élémentaires des groupes montrent que tg est bien une permutation. Soit 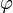\varphi\, l'application de G dans son ensemble d'arrivée, partie de 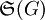\mathfrak{S}(G), définie par :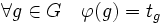

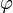\forall g \in G \quad \varphi (g)=t_g\;
  • \varphi\, est un morphisme, en effet:
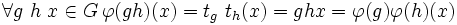
\forall g\ h\ x \in G\, \varphi (gh)(x)=t_g\ t_h (x)= ghx=\varphi (g) \varphi (h)(x)\;
  • Par construction, 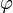\varphi\, est surjective.
  • Montrons alors que 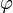\varphi\, est injective. Pour cela considérons g et h deux éléments du groupe. Si tg et th sont égales, alors leurs images de l'élément neutre sont aussi égales et g est égal à h. Ce qui montre que l'application est injective.

Le théorème est ainsi démontré.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Cayley ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de cayley de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Theoreme de Cayley — Théorème de Cayley En théorie des groupes, le théorème de Cayley est un résultat élémentaire affirmant que tout groupe se réalise comme sous groupe d un groupe de permutations : Théorème   Tout groupe G est isomorphe à un sous… …   Wikipédia en Français

  • Théorème de Cayley — En théorie des groupes, le théorème de Cayley[1] est un résultat élémentaire affirmant que tout groupe se réalise comme sous groupe d un groupe de permutations : Théorème   Tout groupe G est isomorphe à un sous groupe du groupe… …   Wikipédia en Français

  • Theoreme de Cayley-Hamilton — Théorème de Cayley Hamilton Pour les articles homonymes, voir Hamilton. En algèbre linéaire, le théorème de Cayley Hamilton (qui porte les noms des mathématiciens Arthur Cayley et William Hamilton) affirme que tout endomorphisme d un espace… …   Wikipédia en Français

  • Théorème de cayley-hamilton — Pour les articles homonymes, voir Hamilton. En algèbre linéaire, le théorème de Cayley Hamilton (qui porte les noms des mathématiciens Arthur Cayley et William Hamilton) affirme que tout endomorphisme d un espace vectoriel de dimension finie sur… …   Wikipédia en Français

  • théorème de Cayley-Hamilton — ● théorème de Cayley Hamilton Théorème selon lequel tout endomorphisme d un K espace vectoriel de dimension n ou toute matrice A de Mn(K) annule son polynôme caractéristique P, soit P(f) = 0 ou P(A) = 0 …   Encyclopédie Universelle

  • Théorème de Cayley-Hamilton —  Ne pas confondre avec le théorème de Cayley en théorie des groupes ni avec le théorème d Hamilton en géométrie. En algèbre linéaire, le théorème de Cayley Hamilton affirme que tout endomorphisme d un espace vectoriel de dimension finie sur… …   Wikipédia en Français

  • Cayley-Hamilton — Théorème de Cayley Hamilton Pour les articles homonymes, voir Hamilton. En algèbre linéaire, le théorème de Cayley Hamilton (qui porte les noms des mathématiciens Arthur Cayley et William Hamilton) affirme que tout endomorphisme d un espace… …   Wikipédia en Français

  • Théorème de Hamilton-Cayley — Théorème de Cayley Hamilton Pour les articles homonymes, voir Hamilton. En algèbre linéaire, le théorème de Cayley Hamilton (qui porte les noms des mathématiciens Arthur Cayley et William Hamilton) affirme que tout endomorphisme d un espace… …   Wikipédia en Français

  • Theoreme de la base incomplete — Théorème de la base incomplète Le théorème de la base incomplète énonce que toute famille libre de vecteurs d un espace vectoriel E peut être complétée pour obtenir une base de E. Sommaire 1 Enoncé 2 Démonstration 2.1 …   Wikipédia en Français

  • Théorème de Baire-Brenef — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”