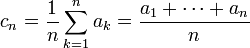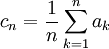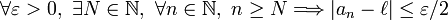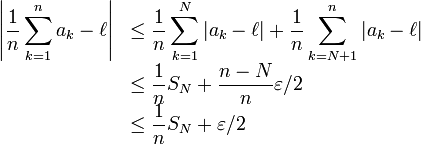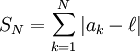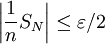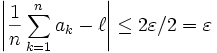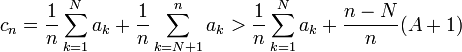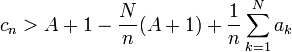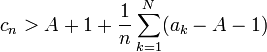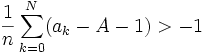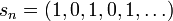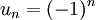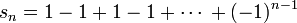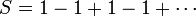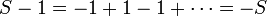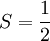Théorème de Cesàro (analyse)

Lemme de Cesàro

En analyse réelle ou complexe, la moyenne de Cesàro d'une suite $(a n)$ est la suite obtenue en effectuant la moyenne arithmétique des n premiers termes de la suite.

Le nom de Cesàro provient du mathématicien italien Ernesto Cesàro.

Le théorème de Cesàro ou lemme de Cesàro précise que, lorsque la suite $(a n)$ a une limite , la moyenne de Cesàro possède la même limite.

Il existe cependant des cas où la suite $(a n)$ ne converge pas et où la moyenne de Cesàro est, elle, convergente. C'est cette propriété qui justifie l'utilisation de la moyenne de Cesàro comme procédé de sommation de série divergente.

Moyenne de Cesàro

Soit une suite 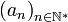$\left( a_n \right)_{n \in \mathbb{N}^*}$ . Alors la moyenne de Cesàro est la suite de terme général :

$c_n=\frac{1}{n}\sum_{k=1}^n a_k=\frac{a_1+\cdots+a_n}{n}$

Le terme d'indice n est ainsi la moyenne arithmétique des n premiers termes de $(a n)$ .

Lemme de Cesàro

Suites convergentes

Théorème de Cesàro — Soit 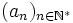$(a_n)_{n\in\mathbb{N^*}}$ une suite de nombres réels ou complexes. Si elle converge vers $\ell$ , alors la suite des moyennes de Cesàro, de terme général

$c_n = \frac{1}{n} \sum_{k=1}^{n} a_k$

converge également, et sa limite est $\ell$ .

Démonstration — Comme $(a n)$ a pour limite $\ell$ , on a

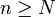$\forall \varepsilon >0,\ \exists N \in \N,\ \forall n \in \N,\ n \geq N \Longrightarrow |a_n-\ell|\leq \varepsilon/2$

Pour $n \geq N$ on a donc

$\begin{array}{ll} \displaystyle \left| \frac{1}{n} \sum_{k=1}^{n} a_k - \ell \right| & \displaystyle \leq \frac{1}{n} \sum_{k=1}^{N} |a_k-\ell | + \frac{1}{n} \sum_{k=N+1}^{n} |a_k-\ell | \\ & \displaystyle \leq \frac{1}{n} S_N + \frac{n-N}{n} \varepsilon/2 \\ & \displaystyle \leq \frac{1}{n} S_N + \varepsilon/2\end{array}$

avec

$S_N=\sum_{k=1}^N |a_k-\ell|$

qui ne dépend pas de $n$ . Donc il existe 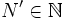$N'\in \N$ tel que pour tout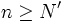 $n \geq N'$

$\left|\frac{1}{n} S_N\right|\leq \varepsilon/2$

Donc pour 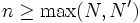$n \geq \max(N,N')$ on a

$\left| \frac{1}{n} \sum_{k=1}^{n} a_k - \ell \right| \leq 2\varepsilon/2=\varepsilon$

donc la suite $(c n)$ converge bien vers $\ell$ .

Limite infinie

Si la suite 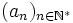$(a_n)_{n\in\mathbb{N^*}}$ est une suite de réels ayant pour limite $+ \infty$ ou $- \infty$ , il en est de même de la suite de ses moyennes de Cesàro.

Démonstration — La démonstration est analogue pour des suites dont la limite est $+ \infty$ ou $- \infty$ . On considère donc une suite réelle $(a n)$ dont la limite est $+ \infty$ .

Donc pour tout réel A, il existe un entier N non nul tel que pour tout k > N , $a k > A + 1$ .

On considère alors la moyenne de Cesàro, pour tout n > N:

$c_n=\frac{1}{n}\sum_{k=1}^N a_k + \frac{1}{n}\sum_{k=N+1}^n a_k > \frac{1}{n}\sum_{k=1}^N a_k + \frac{n-N}{n} (A+1)$

$c_n> A+1 - \frac Nn (A+1) + \frac{1}{n}\sum_{k=1}^N a_k$

$c_n> A+1 + \frac{1}{n}\sum_{k=1}^N (a_k-A-1)$

Pour N fixé, la quantité 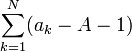$\sum_{k=1}^N (a_k-A-1)$ est constante et 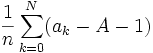$\frac{1}{n}\sum_{k=0}^N (a_k-A-1)$ converge vers 0. Il existe donc un entier N' tel que , pour tout n > N'

$\frac{1}{n}\sum_{k=0}^N (a_k-A-1) > -1$

Donc pour tout n plus grand que N et N' on a $c n > A$ , ce qui prouve que la suite ( $c n$ ) a bien pour limite $+ \infty$ .

Suites divergentes

La réciproque du lemme de Cesàro est fausse : il existe des suites divergentes pour lesquelles la moyenne de Cesàro converge. C'est par exemple le cas de la suite périodique

$s_n=(1,0,1,0,1,\ldots)$

divergente mais qui a pour moyenne de Cesàro 1/2

Application aux séries divergentes

Exemple de la série de Grandi

La série de Grandi est la série associée à la suite

$u_n = (-1)^n\,$

dont les sommes partielles sont

$s_n= 1 - 1 + 1 - 1 + \cdots\, + (-1)^{n-1}$

La série de Grandi est divergente mais la moyenne de Cesàro des sommes partielles converge vers 1/2 (voir plus haut)

On associe alors à la série de Grandi la somme S = 1/2

Euler montra le résultat 1/2 avec une autre méthode^[1] :

Supposons que la somme soit définie, notons la $S$ , alors

$S=1-1+1-1+\cdots$

donc

$S-1=-1+1-1+\cdots=-S$

et donc

$S=\frac{1}{2}$

Utilisations

Une utilisation notable de la moyenne de Cesàro est faite dans le cadre des séries de Fourier. Les sommes de Fejér sont les moyennes de Cesàro des sommes partielles de la série de Fourier. Pour la série de Fourier, les théorèmes de convergence sont délicats. Au contraire les sommes de Fejér vérifient des résultats de convergence très forts, décrits par le théorème de Fejér.

Le produit de Cauchy de deux séries convergentes est une série convergente pour le procédé de sommation de Cesàro.

La moyenne de Cesàro est un procédé de sommation de séries divergentes particulièrement appliqué dans la théorie des séries de Dirichlet. Sur cette question, on consultera le livre de Hardy et Riesz "The general theory of Dirichlet's series".

Généralisation

Il existe plusieurs généralisations de la moyenne de Cesàro, au travers du théorème de Stolz-Cesàro et de la moyenne de Riesz. Le procédé de Cesàro est souvent appelé moyenne (C,1). Pour chaque entier k, il existe une moyenne de Cesàro d'ordre k permettent de sommer des séries divergentes que les procédés (C, n) ne somment pas pour n < k.

Il existe beaucoup d'autres procédés de sommation, comme le procédé de Borel. On consultera notamment le livre de Hardy, "Divergent series" ou le mémorial des sciences mathématiques: Zamansky, la sommation des séries divergentes; Kogbetlianz, Sommation des séries et intégrales divergentes par les moyennes arithmétiques et typiques,

Notes

↑ Pour peu qu'on place la rigueur mathématique de côté : il suppose qu'une entité existe, il en déduit des propriétés... mais cette entité n'existe pas !

Portail des mathématiques

Ce document provient de « Lemme de Ces%C3%A0ro ».

Catégories : Moyenne | Suite | Lemme de mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Cesàro (analyse) de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Théorème de Césaro (analyse) — Lemme de Cesàro En analyse réelle ou complexe, la moyenne de Cesàro d une suite (an) est la suite obtenue en effectuant la moyenne arithmétique des n premiers termes de la suite. Le nom de Cesàro provient du mathématicien italien Ernesto Cesàro.… … Wikipédia en Français
Théorème de cesàro (analyse) — Lemme de Cesàro En analyse réelle ou complexe, la moyenne de Cesàro d une suite (an) est la suite obtenue en effectuant la moyenne arithmétique des n premiers termes de la suite. Le nom de Cesàro provient du mathématicien italien Ernesto Cesàro.… … Wikipédia en Français
Théorème de Cesàro (théorie des nombres) — Ne pas confondre avec le lemme de Cesàro en analyse de suites. En théorie des nombres, le théorème de Cesàro, démontré en 1881 par le mathématicien italien Ernesto Cesàro, établit que la probabilité pour que deux nombres entiers choisis au… … Wikipédia en Français
Theoreme de Stolz-Cesaro — Théorème de Stolz Cesàro En mathématiques, le théorème de Stolz Cesàro est un critère permettant de montrer la convergence d une suite. Soit et deux suites de nombres réels, avec bn strictement croissante et non majorée. Si la limite suivante… … Wikipédia en Français
Théorème de Stolz-Cesàro — En mathématiques, le théorème de Stolz Cesàro est un critère permettant de montrer la convergence d une suite. Soit et deux suites de nombres réels, avec bn strictement croissante et non majorée. Si la limite suivante existe, alors la limite … Wikipédia en Français
Théorème de Fejér — En mathématiques, le théorème de Fejér est un des principaux résultats de la théorie des séries de Fourier. Il donne des propriétés de convergence très générales pour la série de Fourier, dès lors qu on utilise le procédé de sommation de Cesàro.… … Wikipédia en Français
Théorème de l'Hospital — Règle de L Hôpital La règle de L Hôpital (également appelée règle de l Hospital ou règle de Bernoulli) en analyse utilise la dérivée dans le but de déterminer les limites difficiles à calculer de la plupart des quotients. La règle porte le nom d… … Wikipédia en Français
Lemme de Cesàro — Ne pas confondre avec le théorème de Cesàro sur la probabilité que deux nombres entiers soient premiers entre eux. En analyse réelle ou complexe, la moyenne de Cesàro d une suite (an) est la suite obtenue en effectuant la moyenne… … Wikipédia en Français
Lemme De Césaro — Lemme de Cesàro En analyse réelle ou complexe, la moyenne de Cesàro d une suite (an) est la suite obtenue en effectuant la moyenne arithmétique des n premiers termes de la suite. Le nom de Cesàro provient du mathématicien italien Ernesto Cesàro.… … Wikipédia en Français
Lemme de Cesaro — Lemme de Cesàro En analyse réelle ou complexe, la moyenne de Cesàro d une suite (an) est la suite obtenue en effectuant la moyenne arithmétique des n premiers termes de la suite. Le nom de Cesàro provient du mathématicien italien Ernesto Cesàro.… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de Cesàro (analyse)

Lemme de Cesàro

Sommaire

Moyenne de Cesàro