Théorème d'Hurwitz

Théorème d'Hurwitz: Théorème d'Hurwitz

Le Théorème d'Hurwitz est un résultat de mathématiques concernant la théorie des nombres. Il est traite d'approximation diophantienne.

Enoncé

Soit $ε$ un nombre irrationnel, et c un nombre réel positif inférieur ou égal à √5, il existe une infinité de nombres rationnels de la forme a / b avec a et b des nombres entiers premiers entre eux tels que:

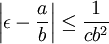
$\left| \epsilon - \frac{a}{b} \right| \leq \frac{1}{c b^2} \,$

De plus, si c est strictement plus grand que √5, il existe des irrationnels ε pour lesquels l'inégalité ci-dessus n'est vérifiée que pour un nombre fini de nombres rationnels.

L'irrationnel qui s' approxime le plus mal par des rationnels au sens précédent est le nombre d'or, égal à (1+ √5)/2. En ce sens, on dit parfois que le nombre d'or est le plus irrationnel des nombres réels.

Toute approximation vérifiant le théorème d'Hurwitz est nécessairement une expression réduite de la fraction continue du nombre. Ce résultat est établi dans l'article Fraction continue.

Démonstration

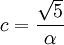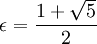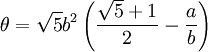Commençons par le deuxième point. Prenons $c = \frac{\sqrt{5}}{\alpha}$ avec $0 < α < 1$ , et $\epsilon = \frac{1+\sqrt{5}}{2}$ . Si $\theta = \sqrt{5} b^2 \left( \frac{\sqrt{5}+1}{2} - \frac{a}{b} \right)$ , alors, on souhaite avoir $| θ | < α$ . En arrangeant les termes et en élevant au carré, on trouve

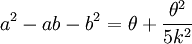$a^2 - ab - b^2 = \theta + \frac{\theta^2}{5k^2} \,$ . Si on considère $P (a) = a 2 - a b - b 2$ comme un polynôme en a, on a 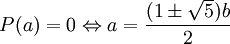$P(a)=0 \Leftrightarrow a = \frac{(1 \pm \sqrt{5})b}{2}$ , mais, comme a et b sont entiers, ce n'est pas possible. Idem pour P(b). Donc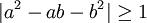 $|a^2 - ab - b^2 | \geq 1 \,$

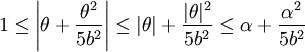
$1 \leq \left| \theta + \frac{\theta^2}{5b^2} \right| \leq |\theta| + \frac{| \theta | ^2}{5b^2} \leq \alpha + \frac{ \alpha ^2}{5b^2}$

Soit encore 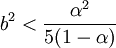$b^2 < \frac{\alpha ^2}{5(1-\alpha )}\,$ , ce qui donne un nombre fini de solutions pour b. Comme a doit vérifié l'inégalité citée dans l'énoncé du théorème, cela donne un nombre fini de nombres rationnels solutions.

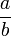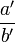Pour la démonstration du premier point, considérons une suite de Farey d'ordre N, avec $\frac{a}{b}$ et $\frac{a'}{b'}$ 2 termes consécutifs tels que 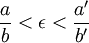$\frac{a}{b} < \epsilon < \frac{a'}{b'}$ . On peut vérifier que :

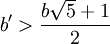
soit $b' > \frac{b \sqrt{5}+1}{2}$

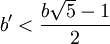
soit $b' < \frac{b \sqrt{5}-1}{2}$

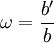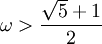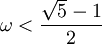Si $\omega = \frac{b'}{b}$ , on a $\omega > \frac{\sqrt{5}+1}{2}$ ou $\omega < \frac{\sqrt{5}-1}{2}$ . On peut montrer que 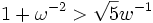$1+\omega ^{-2} > \sqrt{5} w^{-1}$ , d'où

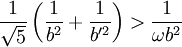$\frac{1}{\sqrt{5}} \left(\frac{1}{b^2} + \frac{1}{b'^2} \right) > \frac{1}{\omega b^2}$ . Mais d'un autre côté, 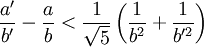$\frac{a'}{b'} - \frac{a}{b} < \frac{1}{\sqrt{5}} \left(\frac{1}{b^2} + \frac{1}{b'^2} \right)$ , ce qui termine l'ébauche de démonstration.

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me d%27Hurwitz ».

Catégories : Théorie des nombres | Théorème de mathématiques

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème d'Hurwitz de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Theoreme d'Hurwitz — Théorème d Hurwitz Le Théorème d Hurwitz est un résultat de mathématiques concernant la théorie des nombres. Il est traite d approximation diophantienne. Enoncé Soit ε un nombre irrationnel, et c un nombre réel positif inférieur ou égal à √5, il… … Wikipédia en Français
Théorème de Hurwitz — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Ne doit pas être confondu avec Théorème d Hurewicz. Il existe plusieurs théorèmes portant le nom du mathématicien Adolf Hurwitz : Théorème de… … Wikipédia en Français
Théorème de Hurwitz (approximation diophantienne) — Pour les articles homonymes, voir Théorème de Hurwitz. En théorie des nombres, le théorème de Hurwitz sur les approximations diophantiennes, établi en 1891 par Adolf Hurwitz, dit que pour tout nombre irrationnel x, il existe une infinité de… … Wikipédia en Français
Théorème de Frobenius généralisé — Pour les articles homonymes, voir Théorème de Hurwitz. Le théorème de Frobenius généralisé (connu également sous le nom de théorème de Hurwitz[1], bien que ce dernier en soit une forme plus générale encore) est un théorème d algèbre générale qui… … Wikipédia en Français
Théorème d'Hurewicz — Ne doit pas être confondu avec Théorème de Hurwitz. En topologie algébrique, le théorème d Hurewicz est une description du premier groupe d homologie singulière d un espace topologique X à l aide du groupe fondamental de X. Il a été… … Wikipédia en Français
Théorème de Roth — Le théorème de Roth, ou théorème de Thue Siegel Roth, est un énoncé de théorie des nombres, concernant plus particulièrement l approximation diophantienne. Le résultat est le suivant : Pour tout nombre algébrique α et pour tout ε > 0, l… … Wikipédia en Français
HURWITZ (A.) — HURWITZ ADOLF (1859 1919) Élève de Felix Klein, Adolf Hurwitz représentait une tendance unificatrice en mathématiques. Avec ses étudiants Hilbert et Minkowski, il s’éleva contre le partage abusif des mathématiques en de nombreuses branches, non… … Encyclopédie Universelle
Theoreme isoperimetrique — Théorème isopérimétrique En géométrie, un théorème isopérimétrique traite d une question concernant les compacts d un espace métrique muni d une mesure. Un exemple simple est donné par les compacts d un plan euclidien. Les compacts concernés sont … Wikipédia en Français
Théorème des quatre carrés de Lagrange — Le théorème des quatre carrés de Lagrange, est également connu sous le nom de conjecture de Bachet ; il a été énoncé pour la première fois par Claude Gaspard Bachet de Méziriac en 1621, dans les notes accompagnant sa traduction en latin du… … Wikipédia en Français
Théorème isopérimétrique — En géométrie, un théorème isopérimétrique traite d une question concernant les compacts d un espace métrique muni d une mesure. Un exemple simple est donné par les compacts d un plan euclidien. Les compacts concernés sont ceux de mesures finies… … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts