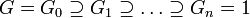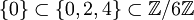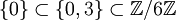Théorème Jordan-Hölder

Théorème Jordan-Hölder

Théorème de Jordan-Hölder

Sommaire

Définition

Soit G un groupe. On appelle suite de composition de G toute suite finie de sous-groupes 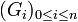(G_{i})_{0 \leq i \leq n} telle que

G = G_{0} \supseteq G_{1} \supseteq \ldots \supseteq G_{n} = 1

et que, pour chaque i (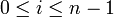0 \leq i \leq n-1), Gi + 1 soit distingué dans Gi.

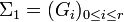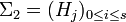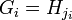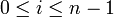Soient \Sigma _{1} = (G_{i})_{0 \leq i \leq r} et \Sigma _{2} = (H_{j})_{0 \leq i \leq s} deux suites de composition d'un même groupe G. On dit que Σ2 est un raffinement de Σ1, ou encore que Σ2 est plus fine que Σ1, si Σ1 est extraite de Σ2, c'est-à-dire s'il existe des indices 0 = j0 < j1 ... < jr = s tels que G_{i} = H_{j_{i}} pour tout i (0 \leq i \leq n-1).

Soit Σ une suite de composition d'un groupe G. Les deux conditions suivantes sont équivalentes :
a) Σ est strictement décroissante et n'admet pas d'autre raffinement strictement décroissant qu'elle-même;
b) les quotients de Σ sont tous des groupes simples.

On appelle suite de Jordan-Hölder une suite de composition dont tous les quotients sont des groupes simples, ou, ce qui revient au même, une suite de composition strictement décroissante qui n'a pas d'autre raffinement strictement décroissant qu'elle-même.

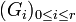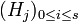Soient (G_{i})_{0 \leq i \leq r} et (H_{j})_{0 \leq i \leq s} deux suites de composition d'un même groupe G. On dit que ces deux suites de composition sont équivalentes si r = s et qu'il existe une permutation σ de l'ensemble 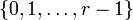\{0, 1, \ldots , r-1\} telle que pour tout i (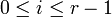0 \leq i \leq r-1), le quotient Gi / Gi + 1 soit isomorphe au quotient Hσ(i) / Hσ(i) + 1.

Exemples

  • Pour tout groupe G non trivial (c'est-à-dire non réduit à l'élément neutre), la suite G, {e} est une suite de composition. C'est une suite de Jordan-Hölder si et seulement si G est simple.
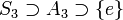  • S _ 3 \supset A _ 3 \supset \{e\} est une suite de Jordan-Hölder.
  • On démontre que si un groupe admet une suite de Jordan-Hölder, toute suite de composition de ce groupe admet un raffinement qui est une suite de Jordan-Hölder.
  • Un groupe est résoluble si et seulement il admet une suite de composition dont tous les quotients (Gi+1/Gi) sont commutatifs. On prouve que si un groupe résoluble G admet une suite de Jordan-Hölder (ce qui est le cas si G est fini), chaque groupe quotient de cette suite est cyclique d'ordre premier (et G est donc fini). Galois montra qu'une équation polynomiale à une variable est résoluble par radicaux si et seulement si son groupe de Galois est résoluble.
  • Tout groupe fini admet une suite de Jordan-Hölder.

Le théorème de Jordan-Hölder

Deux suites de Jordan-Hölder d'un même groupe sont toujours équivalentes.

Exemples

  • Pour le groupe des nombres modulo 6, on a les deux suites de Jordan-Hölder suivantes :
    • \left\{ 0 \right\} \subset \left\{ 0 , 2 , 4 \right\} \subset \mathbb Z / 6 \mathbb Z
    • \left\{ 0 \right\} \subset \left\{ 0 , 3 \right\} \subset \mathbb Z / 6 \mathbb Z

dont les quotients sont Z/3Z puis Z/2Z pour la première et Z/2Z puis Z/3Z pour la seconde.

Généralisation

Dans le cadre des catégories (ou structures), on peut généraliser le concept des suites de Jordan-Hölder en remplaçant les inclusions par les monomorphismes (ou fonctions injectives) qui permettent d'avoir un quotient. Mais on n'a pas forcément le théorème de Jordan-Hölder.

  • Ainsi dans le cadre des espaces vectoriels un drapeau est une suite de Jordan-Hölder maximale, les quotients étant à chaque fois un espace vectoriel de dimension 1. Le théorème est valide et la taille d'une suite maximale est la dimension de l'espace vectoriel.

Liens externes

(en) Could Jordan have proved the Jordan-Hölder theorem? par Dirk Schlimm

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Jordan-H%C3%B6lder ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème Jordan-Hölder de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Theoreme de Jordan-Holder — Théorème de Jordan Hölder Sommaire 1 Définition 1.1 Exemples 2 Le théorème de Jordan Hölder 2.1 Exemples …   Wikipédia en Français

  • Théorème de jordan-hölder — Sommaire 1 Définition 1.1 Exemples 2 Le théorème de Jordan Hölder 2.1 Exemples …   Wikipédia en Français

  • Théorème de Jordan-Hölder — Sommaire 1 Définition 1.1 Exemples 2 Le théorème de Jordan Hölder 2.1 Exemples 3 …   Wikipédia en Français

  • JORDAN (C.) — Le mathématicien français Camille Jordan fut le spécialiste indiscuté de la théorie des groupes pendant toute la fin du XIXe siècle et on lui doit de très nombreux résultats, tant sur les groupes finis que sur les groupes dits classiques, dont il …   Encyclopédie Universelle

  • Theoreme de Kronecker — Théorème de Kronecker Leopold Kronecker En mathématiques et plus particulièrement en algèbre, le théorème de Kronecker traite des groupes abéliens finis. Le théorème de Kronecker est aussi appelé théorème fondamental des groupes abéliens finis.… …   Wikipédia en Français

  • Théorème de kronecker — Leopold Kronecker En mathématiques et plus particulièrement en algèbre, le théorème de Kronecker traite des groupes abéliens finis. Le théorème de Kronecker est aussi appelé théorème fondamental des groupes abéliens finis. Il stipule que tout… …   Wikipédia en Français

  • Théorème de Kronecker — Cet article concerne la structure des groupes abéliens finis. Pour d autres notions ou résultats portant le nom de Kronecker, voir Leopold Kronecker. Leopold Kronecker En a …   Wikipédia en Français

  • Holder — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Holder peut désigner : Holder, un poste au football américain. Patronyme Holder est un nom de famille notamment porté par : Eric Holder (né en… …   Wikipédia en Français

  • Théorème de Gauss-Lucas — Pour les articles homonymes, voir Théorème de Gauss. En mathématiques, le théorème de Gauss Lucas, ou théorème de Lucas, établit une propriété des polynômes complexes. Il énonce que les racines du polynôme dérivé sont situées dans l enveloppe… …   Wikipédia en Français

  • Lemme de Jordan —  Ne pas confondre avec le théorème de Jordan en topologie ni avec le théorème de Jordan Hölder ou la réduction de Jordan en algèbre. En mathématiques, le lemme de Jordan est un lemme utilisé essentiellement pour le calcul d intégrales par le …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”