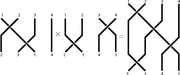Groupe de tresses

Groupe de tresses

Théorie des tresses

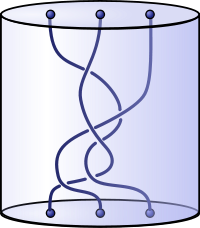
La théorie des tresses est l'étude des tresses, objet mathématique formalisant ce qu'on appelle tresse (ou natte) dans la vie courante. Loin d'être une simple distraction mathématique, les tresses ont une structure de groupe naturelle, et possèdent des liens profonds avec des domaines divers des mathématiques et de la physique : topologie, théorie des noeuds, algèbre, combinatoire algébrique, physique statistique[réf. nécessaire]...

Renoir:La Natte

Sommaire

Définitions

Les groupes de tresses peuvent être définis de différentes manières équivalentes, illustrant les relations qu'ils entretiennent avec différents domaines des mathématiques.

Tresses géométriques

Exemple de tresse à trois brins

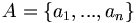Soit A = \left\{a_1, ..., a_n\right\} un ensemble de n points de \mathbb{D} le disque unité ouvert de \mathbb{C}.

On appelle brin le graphe d'une application b continue de I=\left[0,1\right] dans le disque unité ouvert de \mathbb{C}, dont les extrémités b(0) et b(1) appartiennent à A.

On appelle tresse géométrique à n brins la réunion de n brins disjoints. On considère que deux tresses géométriques représentent la même tresse "abstraite" si elle peuvent être obtenue l'une à partir de l'autre en bougeant les brins continument, sans que les brins ne se traversent ni ne se détachent à leurs extrémités. On dit alors que les deux tresses géométriques sont isotopes.

On définit une loi de composition sur l'ensemble des tresses géométriques, telle que le produit de deux tresses est obtenus simplement en les empilant l'une au-dessus de l'autre. Ce produit est associatif et compatible avec la relation d'isotopie. Le produit d'une tresse avec son image dans un miroir horizontal est isotope à la tresse triviale (sans croisement), dont la classe d'équivalence joue le rôle d'élément neutre. Ceci permet donc également de définir l'inverse d'une tresse. Finalement, l'ensemble des tresses géométriques à n brins quotienté par la relation d'isotopie est un groupe, noté Bn.

Produit de deux tresses

Générateurs et relations

Le groupe de tresses 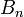\, B_n est le groupe engendré par les générateurs 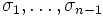\, \sigma_1,\dots,\sigma_{n-1} et les relations

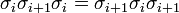  1. \, \sigma_i\sigma_{i+1}\sigma_i=\sigma_{i+1}\sigma_i\sigma_{i+1} si \, |i-j|=1
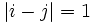
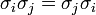  2. \, \sigma_i\sigma_j=\sigma_j\sigma_i sinon.

Groupe fondamental

On définit ce qu'on appelle un espace de configuration 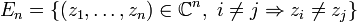E_n=\{(z_1,\dots,z_n) \in \mathbb{C}^n,\ i\neq j \Rightarrow z_i \neq z_j \}. Autrement dit, cet espace est l'ensemble des n-uplets de nombres complexes dont tous les éléments sont distincts. On peut interpreter physiquement cet espace en remarquant qu'un nombre complexe représente les coordonnées d'un point dans un plan, ainsi l'espace de configuration 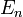\, E_n peut être vu comme l'ensemble des configurations dans lesquelles peuvent se trouver n particules dans un plan (la condition refletant simplement le fait que deux particules ne peuvent pas se trouver au meme endroit).

On remarque par ailleurs qu'en général, les brins d'une tresse n'arrivent pas dans le meme ordre qu'au départ. Par exemple, sur le premier dessin, le brin qui part d'en haut à gauche arrive en bas à droite. Il existe par contre des tresses dont tous les brins arrivent à la meme position que celle dont ils sont partis. Une telle tresse est appelée tresse pure. L'ensemble des tresses pures forme un sous groupe du groupe de tresses.

Le lien entre ces deux notions est le suivant : le groupe fondamental de 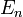\, E_n est le groupe de tresses pures à n brins, noté \, P_n.

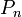Mots de tresse

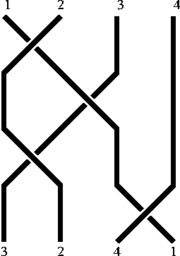
A isotopie près, une tresse abstraite peut toujours être représentée par une tresse géométrique qui ne contient jamais deux croisement à la même hauteur. Il est donc possible de projeter toute tresse dans le plan, afin d'obtenir un diagramme de tresse. Afin de ne pas perdre d'information vis-à-vis de l'espace en 3 dimensions il faut indiquer, lorsque deux brins se croisent, lequel passe devant l'autre.

Diagramme d'une tresse

Remarque

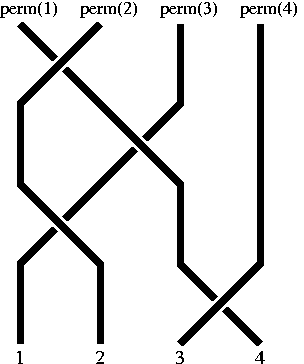
Pour que les diagrammes de tresses et leur produit correspondent aux permutations et à leur composition il faut lire les diagrammes de tresses de bas en haut. Par exemple, le diagramme de tresses ci-dessus a pour permutation \, (1 4 3).

Tresse1t.png

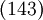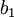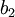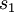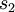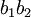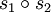Ainsi prenons deux diagrammes de tresses \, b_1 et \, b_2 de permutation associée respective \, s_1 et \, s_2. Le produit \, b_1b_2 a pour permutation \, s_1\circ s_2.


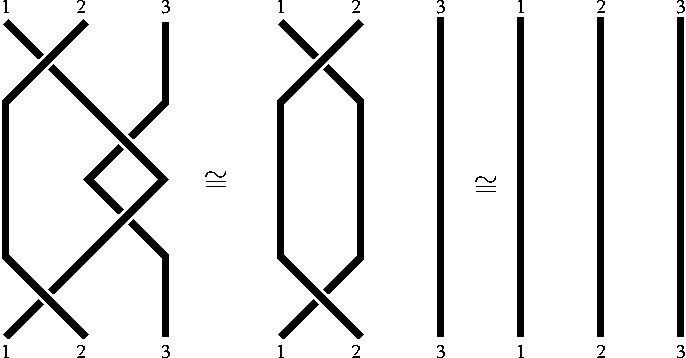
Pour étudier les tresses, il faut les comparer vis-à-vis de leur chemin et de leur permutation associée. Dans un diagramme de tresses, certains croisements sont indépendants les uns des autres.

Tresse2b.png

Deux diagrammes de tresses sont dits 'isotopes' si on peut obtenir l'un à partir de l'autre en déplaçant les brins sans les « couper » et sans toucher aux extrémités.


La relation d'isotopie sur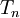 \, T_n est une relation d'équivalence.


Deux diagrammes de tresses isotopes représentent la même permutation, mais la réciproque est fausse : deux diagrammes ayant la même permutation associée ne sont pas nécessairement isotopes.

Tresse7.png

Groupe de tresses à n brins

En quotientant 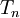\, T_n par la relation d'isotopie on obtient une structure de groupe sur l'ensemble des diagrammes de tresses à 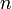\, n brins. On note 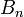\, B_n et on appelle « groupe de tresse à n brins » le groupe ainsi obtenu. L'élément neutre étant bien évidemment la classe du diagramme trivial, l'inverse d'un diagramme est le diagramme obtenu en prenant son image miroir.

Fichier:TresseInv.ps

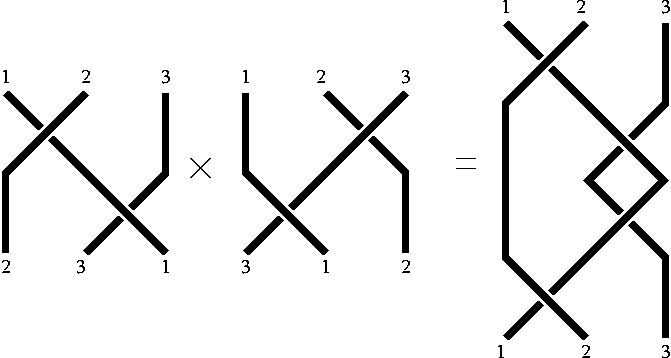
Tresse6.png

Tresse6b.png

Par simplification on appelle tresse à 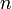\, n brins un élément de \, B_n.

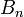Groupe de tresses

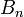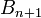On plonge \, B_n dans \, B_{n+1} en transformant les tresses à 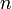\, n brins en tresses à 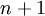\, n+1 brins de la manière suivante. On ajoute à droite un 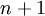\, n+1ème brins qui n'en croise aucun autre, comme on le voit dans l'exemple suivant: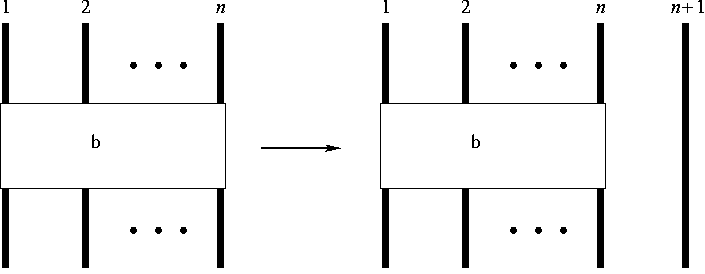

Plonge.png

On note 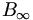B_{\infty} le groupe

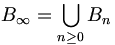B_{\infty}=\bigcup_{n\geq 0}B_n.

Applications et généralisations

Les groupes de tresses comme groupes fondamentaux

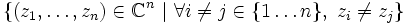
Le groupe de tresse pur à n brins est isomorphe au groupe fondamental de l'espace de configuration \left \{ (z_1,\dots,z_n) \in \mathbb{C}^n \ |\ \forall i \neq j \in \{1\dots n\},\ z_i \neq z_j \right\}

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9orie des tresses ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Groupe de tresses de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Groupe Symétrique — Cette notion est différente de celle de groupe de symétrie. En mathématiques, plus particulièrement en algèbre, le groupe symétrique d un ensemble E est le groupe des permutations de E, c est à dire des bijections de E sur lui même. Sommaire 1… …   Wikipédia en Français

  • Groupe de permutation — Groupe symétrique Cette notion est différente de celle de groupe de symétrie. En mathématiques, plus particulièrement en algèbre, le groupe symétrique d un ensemble E est le groupe des permutations de E, c est à dire des bijections de E sur lui… …   Wikipédia en Français

  • Groupe des permutations — Groupe symétrique Cette notion est différente de celle de groupe de symétrie. En mathématiques, plus particulièrement en algèbre, le groupe symétrique d un ensemble E est le groupe des permutations de E, c est à dire des bijections de E sur lui… …   Wikipédia en Français

  • Groupe symetrique — Groupe symétrique Cette notion est différente de celle de groupe de symétrie. En mathématiques, plus particulièrement en algèbre, le groupe symétrique d un ensemble E est le groupe des permutations de E, c est à dire des bijections de E sur lui… …   Wikipédia en Français

  • Tresses (mathématiques) — En mathématiques, et plus précisément en topologie et théorie des groupes, une tresse est un objet mathématique formalisant ce qu on appelle tresse (ou natte) dans la vie courante. Les tresses ont une structure de groupe naturelle, et possèdent… …   Wikipédia en Français

  • Groupe symétrique — Cette notion est différente de celle de groupe de symétrie. En mathématiques, plus particulièrement en algèbre, le groupe symétrique d un ensemble E est le groupe des permutations de E, c est à dire des bijections de E sur lui même. Un sous… …   Wikipédia en Français

  • Tresses — 44° 50′ 58″ N 0° 27′ 46″ W / 44.8494444444, 0.462777777778 …   Wikipédia en Français

  • Theorie des tresses — Théorie des tresses La théorie des tresses est l étude des tresses, objet mathématique formalisant ce qu on appelle tresse (ou natte) dans la vie courante. Loin d être une simple distraction mathématique, les tresses ont une structure de groupe… …   Wikipédia en Français

  • Théorie des tresses — La théorie des tresses est l étude des tresses, objet mathématique formalisant ce qu on appelle tresse (ou natte) dans la vie courante. Loin d être une simple distraction mathématique, les tresses ont une structure de groupe naturelle, et… …   Wikipédia en Français

  • Presentation d'un groupe — Présentation d un groupe En théorie des groupes, un groupe peut se définir par sa présentation autrement dit la donnée d un ensemble de générateurs et de relations que ceux ci doivent vérifier. La possibilité de cette définition découle de ce que …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”