Paradoxe du compresseur

Le paradoxe du compresseur s'applique à tout compresseur de données informatiques sans perte. Il exprime qu'un compresseur sans perte universel ne peut pas exister. Plus précisément, pour tout compresseur sans perte, on est certain que :

1. il est impossible de compresser strictement tous les mots ;
2. s'il existe un mot qui est strictement compressé alors il existe un autre mot dont la version compressée est strictement plus grande que le mot lui-même ;
3. pour n'importe quel mot de départ auquel on applique de manière répétée le compresseur, on est nécessairement dans l'un des cas de figure suivants

• soit une suite de mots se répète infiniment,
• soit les mots successifs obtenus atteignent des tailles arbitrairement grandes.

Ces propriétés sont démontrées ci-après. Cependant, elles n'enlèvent rien à l'intérêt des compresseurs sans perte. En effet, dans la pratique, les mots, messages ou fichiers que l'on souhaite compresser ne sont pas quelconques et choisis aléatoirement parmi tous les mots, messages ou fichiers possibles. Les compresseurs se servent de leurs particularités. Des compresseurs seront alors très bons avec certains types de données, et très mauvais avec d'autres.

Ainsi pour ces types de compresseurs spécialisés, l'information fournie par le contexte est utilisée pour la compression (voir théorie de l'information).

Historique

Lorsque fut lancé par IBM son système OS/2, les lecteurs de CD n'étaient pas généralisés et le système était fourni sur 17 disquettes, ce qui en rendait l'installation pénible. À une demande de la direction soucieuse de savoir si l'on pouvait réduire cette taille, la légende dit que la réponse aurait été : « Nous pouvons le faire tenir compressé sur une seule disquette, mais à l'aide d'un compresseur si complexe qu'il en occupera seize ». C'était là le fameux paradoxe initial.

La notion de complexité de Kolmogorov n'était pas loin.

Expérimentation

On peut aisément vérifier expérimentalement ce paradoxe. Voici un script shell qui crée un fichier comportant 100 fois la ligne "blabla" puis qui effectue 100 compressions successives de ce fichier à l'aide du compresseur Gzip et enfin affiche les tailles successives obtenues :

for i in `seq 1 100`; do echo "blabla" >> toto001; done
for i in `seq 1 100`; do gzip -c "toto`printf "%03d" $i`" > "toto`printf "%03d" $((i+1))`"; done
wc -c toto*

On vérifie souvent en pratique qu'un fichier qui est déjà le résultat d'une compression se compresse mal, voire grossit par application du compresseur. D'ailleurs, Gzip refuse par défaut de compresser les fichiers comportant l'extension ".gz" qui est le signe d'une précédente application de ce compresseur.

Preuve mathématique

Un compresseur sans perte peut être vu comme une injection des mots dans les mots, c'est-à-dire une fonction C telle que

C(u) = C(v) implique u = v.

On vérifie alors aisément que, pour tout mot u, l'un des deux cas suivants est vérifié :

1. la suite (Cⁿ(u))_n est périodique,
2. la suite (Cⁿ(u))_n ne contient jamais deux fois le même mot et donc pour tout entier 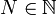il existe un entier k tel que le mot C^k(u) est de taille supérieure à N.

Ceci montre la troisième propriété du paradoxe énoncé ci-dessus. Les deux premières en découlent car, s'il y a compression stricte, c'est-à-dire s'il existe un mot u plus grand que sa version compressée C(u), alors :

• soit u est dans un cycle de longueur k et il existe 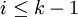tel que le mot Cⁱ(u) est strictement plus petit que sa version compressée C^{i + 1}(u),
• soit la suite (Cⁿ(u))_n ne contient jamais deux fois le même mot donc elle contient un mot strictement plus petit que sa version compressée (car on ne peut pas avoir une suite infinie décroissante, au sens large, de mots tous distincts).

On peut remarquer par ailleurs qu'il est impossible de compresser strictement tous les mots d'une taille N donnée : en effet il y a a^N mots de taille N pour un alphabet à a lettres et seulement 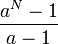mots avec strictement moins de N lettres.

Un autre paradoxe

Un autre paradoxe célèbre concernant les compresseurs est le suivant :

Pour tout mot, il existe un compresseur qui le compresse en un mot de 1 bit.

Cela rappelle qu'une signification n'est pas portée par un message en soi, mais par un doublet message/décodeur. Ces idées ont été poussées très loin avec la théorie de la complexité de Kolmogorov.

Exemple avec Guerre et Paix

Est-il possible de compresser le roman Guerre et Paix en un seul bit ? Oui, avec le décompresseur suivant :

si bit[0] = 1
alors { impression de Guerre et paix (le roman, pas le titre)}
sinon { écriture des bits suivants, qui constituent le message }

Là encore, on reporte sur la complexité du compresseur ce qui a été économisé dans le message, donc sans bénéfice particulier.

Voir aussi

Articles connexes

• Compression de données
• NABOB
• BARF

Liens externes

• Sean McGrath a résumé la situation de façon lapidaire sous la forme : The library is the language ("La bibliothèque est le langage").