Theorie de la decision

Theorie de la decision: Théorie de la décision

La théorie de la décision est une théorie de mathématiques appliquées ayant pour objet la prise de décision en univers risqué.

Sommaire

1 Les limites de la théorie des probabilités

2 Risque ou incertitude ?

3 Gain non quantifiable

4 La théorie de la décision dans le risque

5 La théorie de la décision dans l'incertain

6 Notes

7 Voir aussi

7.1 Auteurs

7.2 Articles connexes

7.3 Bibliographie

Les limites de la théorie des probabilités

En présences de choix, la théorie des probabilités propose de calculer les espérances mathématiques de gain et d'opter pour le choix qui maximise cette espérance de gain. Cependant ce procédé a plusieurs limites. La théorie de la décision vise à apporter une réponse à ces cas limites.

Risque ou incertitude ?

En théorie de la décision, on distingue le risque de l'incertitude. Le risque désigne une situation dans laquelle les distributions de probabilités sur les résultats existent et sont connues des agents : c'est par exemple le cas du loto ou d'un lancer de dés. L'attitude vis-à-vis du risque d'un décideur est cruciale pour comprendre son comportement face à des situations risquées. Considérons le choix de participer à un jeu où le joueur a une chance sur dix de gagner cent fois sa mise. L'espérance de gain est très positive et tout joueur serait prêt à miser 1 euro ; mais qui ferait le choix de jouer si la mise obligatoire était toute la fortune du joueur ?^[1] Dans le premier cas, on parlera d'aversion pour le risque et dans le second cas, de préférence pour le risque. Le comportement normal est une certaine aversion au risque^[2].

Si les situations de risque constituent, dans la vie courante, des situations assez marginales, l'incertitude est en revanche omniprésente. Elle désigne les situations dans lesquelles les distributions de probabilités n'existent pas ou ne sont pas connues des agents. C'est par exemple le cas d'une course de chevaux : sur quel cheval parier sachant que l'on ne connaît pas la probabilité qu'a chaque cheval de gagner ? La théorie de la décision est également capable d'apporter des réponses à ce type de situation.

Gain non quantifiable

D'autre part, dans de nombreux cas, les gains ne sont pas quantifiables (voir l'exemple du pari de Pascal, ou de l'assurance vie), difficilement mesurable (comme les catastrophes) ou difficilement comparables. Là encore, la théorie de la décision cherche à apporter des réponses, à établir des préférences.

La théorie de la décision dans le risque

Optimisation et maximalisation sont les deux mots-clés définissant les théories de la prise de décision basées sur la rationalisation, c’est-à-dire les théories définissant les normes logiques et rationnelles que tous les preneurs de décisions sont censés suivre pour que le choix soit celui qui "rapporte" le plus. La théorie de l'utilité espérée est l'approche la plus communément retenue par la théorie de la décision pour décrire les choix risqués. Introduisons d'abord quelques notations:
L'incertitude est décrite par un ensemble d'états du monde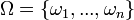 $\Omega=\left\{ \omega_{1},...,\omega_{n}\right\}$ partitionné par la famille de parties ${\textstyle \mathcal{P}(\Omega)=2^{n}}$ .
Un élément de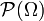 ${\textstyle \mathcal{P}(\Omega)}$ est appelé événement.
Une variable aléatoire $f$ est une fonction qui associe à chaque $ω$ un résultat noté $x$ .
L'ensemble des résultats est noté $X$ , $X$ étant un sous-ensemble de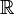 ${\textstyle \mathbb{R}}$ .
On écrit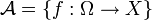 ${\textstyle \mathcal{A}=\left\{ f:\Omega\rightarrow X\right\} }$ l'ensemble des variables aléatoires.
Dans le cas du risque, le décideur est supposé connaître les distributions de probabilités induites par les variables aléatoires. La distribution induite par la variable aléatoire $f$ est notée $l f$ . La relation binaire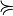 $\succcurlyeq$ signifie "est préféré ou indifférent à". Elle compare des loteries (ou distributions de probabilités), c'est à dire des projets risqués de la forme $l = (x 1, p 1;...; x n, p n)$ où 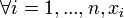$\forall i=1,...,n,x_i$ est le résultat obtenu avec la probabilité $p i$ . On écrit $\mathcal{L}=\left\{ l_{f}:X\rightarrow\left[0;1\right]\mid{\textstyle f\in\mathcal{A}},\sum_{i=1}^{i=n}l_{f}(x_{i})=1\right\}$ l'ensemble des distributions de probabilités. 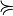La règle de décision développée par Von Neumann et morgenstern en 1944, connue sous le nom "d'utilité espérée", repose sur les hypothèses suivantes, qui sont appelées axiomes et sont postulées sur la relation $\succcurlyeq$ .

Axiome 1 (préordre total). 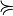$\succcurlyeq$ est un préordre total. Cela signifie que :

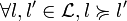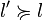$\forall l,l^{\prime}\in\mathcal{L},l\succcurlyeq l^{\prime}$ ou $l^{\prime}\succcurlyeq l$ (totalité);

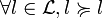${\textstyle \forall l\in\mathcal{L}},l\succcurlyeq l$ (réflexivité);

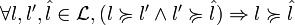${\textstyle \forall l,l^{\prime},\hat{l}\in\mathcal{L},(l\succcurlyeq l^{\prime}\wedge l^{\prime}\succcurlyeq\hat{l})\Rightarrow l\succcurlyeq\hat{l}}$ (transitivité).

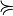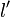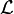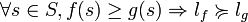Axiome 2 (Monotonie). $\succcurlyeq$ est monotone si pour toutes loteries $l$ et $l^{\prime}$ dans ${\textstyle \mathcal{L}}$ on a $\forall s\in S,f(s)\geq g(s)\Rightarrow l_{f}\succcurlyeq l_{g}$ .

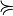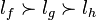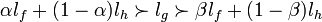Axiome 3 (Continuité). $\succcurlyeq$ est continue si pour toutes loteries $l f, l g$ et $l h$ telles que $l_{f}\succ l_{g}\succ l_{h}$ , $\exists \alpha,\beta\in\left]0;1\right[$ tels que : ${\textstyle \alpha l_{f}+(1-\alpha)l_{h}\succ l_{g}\succ\beta l_{f}+(1-\beta)l_{h}}$ .

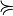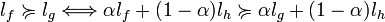
Axiome 4 (Indépendance). $\succcurlyeq$ est indépendante si pour tout $α$ dans $\left[0;1\right]$ et pour toutes loteries $l f, l g$ et $l h$ on a : $l{}_{f}\succcurlyeq l_{g}\Longleftrightarrow\alpha l_{f}+(1-\alpha)l_{h}\succcurlyeq\alpha l_{g}+(1-\alpha)l_{h}$

Nous pouvons maintenant présenter le théorême de représentation de Von Neumann et Morgenstern :

Théorême. Etant donnée une relation de préférences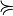 $\succcurlyeq$ , les deux propositions suivantes sont équivalentes: (i) 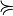$\succcurlyeq$ satisfait les axiomes 1-4; (ii) Il existe une fonction à valeurs réelles 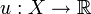$u:X\rightarrow\mathbb{R}$ positive à une transformation affine croissante près tel que la valeur d'une loterie $l = (x 1, p 1;...; x n, p n)$ est donnée par 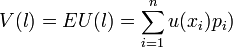$V(l)=EU(l)=\sum_{i=1}^{n}u(x_{i})p_{i})$ et $\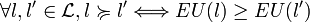forall l,l^{\prime}\in\mathcal{L},l\succcurlyeq l^{\prime}\Longleftrightarrow EU(l)\geq EU(l^{\prime})$ .

La fonction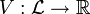 ${\textstyle V:\mathcal{L}\rightarrow\mathbb{R}}$ est donc une fonction d'espérance d'utilité (EU).

Le contenu descriptif du modèle de décision EU a été rapidement critiqué dans une expérience restée cèlèbre sous le nom de "paradoxe d'Allais". La version présentée ici est celle de Kahneman et Tversky (1979). Les sujets doivent choisir entre deux paires de loteries. D'une part, entre $l 1 = (3000,1)$ et $l 2 = (0,0.2;4000,0.8)$ et, d'autre part, entre $l 3 = (0,0.75;3000,0.25)$ et $l 4 = (0,0.8;4000,0.2)$ . Le choix le plus fréquemment observé est $l 1$ dans la première paire et $l 4$ dans la seconde paire, en contradiction avec les prédictions de la fonction EU(.). Plus spécifiquement, c'est l'axiome d'indépendance qui est violé par les individus. Pour résoudre ce paradoxe, une réponse courante consiste à supposer que le traitement des probabilités n'est pas linéaire. Les individus "déforment" les probabilités en fonction des résultats (par exemple, ils sous-estiment la probabilité d'obtenir 3000 dans la loterie $l 3$ ). Principalement axiomatisé par Quiggin (1982), le modèle suivant, appelé "Rank-Dependent Expected Utility " (RDEU), repose principalement sur un affaiblissement de l'axiome d'indépendance. Celui-ci ne tient plus que sur les distributions de probabilités induites par les variables aléatoires ayant le même tableau de variation, c'est-à-dire qui sont communément monotones, ou encore comonotones :

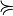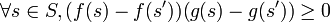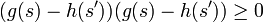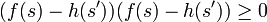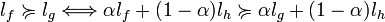
Axiome 4' (Indépendance comonotone). $\succcurlyeq$ est indépendante pour les variables aléatoires comonotones si pour tout $α$ dans $\left[0;1\right]$ et pour toutes loteries $l f, l g$ et $l h$ telles que $\forall s \in S, (f(s)-f(s^{\prime}))(g(s)-g(s^{\prime})) \geq 0$ , $(g(s)-h(s^{\prime}))(g(s)-h(s^{\prime})) \geq 0$ et $(f(s)-h(s^{\prime}))(f(s)-h(s^{\prime})) \geq 0$ on a : $l{}_{f}\succcurlyeq l_{g}\Longleftrightarrow\alpha l_{f}+(1-\alpha)l_{h}\succcurlyeq\alpha l_{g}+(1-\alpha)l_{h}$

Théorême. Etant donnée une relation de préférences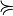 $\succcurlyeq$ , les deux propositions suivantes sont équivalentes : (i) 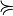$\succcurlyeq$ satisfait les axiomes 1-3 et l'axiome 4'; (ii) Il existe une fonction à valeurs réelles 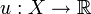$u:X\rightarrow\mathbb{R}$ positive à une transformation affine croissante près et une fonction à valeurs réelles croissante $\phi:\left[0;1\right]\rightarrow\left[0;1\right]$ telle que la valeur d'une loterie $l = (x 1, p 1;...; x n, p n)$ est donnée par $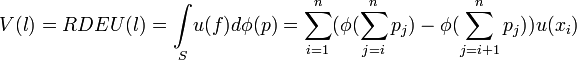V(l)=RDEU(l)=\underset{S}{\int}u(f)d\phi(p)=\sum_{i=1}^{n}(\phi(\sum_{j=i}^{n}p_{j})-\phi(\sum_{j=i+1}^{n}p_{j}))u(x_{i})$ et $\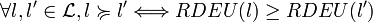forall l,l^{\prime}\in\mathcal{L},l\succcurlyeq l^{\prime}\Longleftrightarrow RDEU(l)\geq RDEU(l^{\prime})$ .

La théorie de la décision dans l'incertain

L'utilité espérée a été élargie dès 1954 par L.J. Savage aux situations incertaines. Ses postulats, au nombre de 6 dans le cas où $Ω$ est fini, sont les suivants :

Axiome 1 (préordre complet). 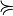$\succcurlyeq$ est un préordre complet.

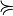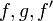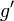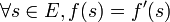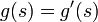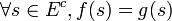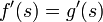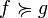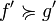Axiome 2 (Principe de la chose sûre). $\succcurlyeq$ est telle que pour tout événement $E$ et actes $f,g,f^{\prime}$ et $g^{\prime}$ tels que $\forall s \in E, f(s)=f^{\prime}(s)$ et $g(s)=g^{\prime}(s)$ , et $\forall s \in E^{c}, f(s)=g(s)$ et $f^{\prime}(s)=g^{\prime}(s)$ , $f\succcurlyeq g$ si et seulement si $f^{\prime}\succcurlyeq g^{\prime}$ .

Notes

↑ À l'inverse, le loto a de nombreux émules bien que son espérance de gain soit négative.

↑ Le goût du risque est considéré comme une pathologie du joueur.

Voir aussi

Information Partielle Linéaire

Auteurs

Herbert Simon

Bernard Roy

Articles connexes

Paradoxe de Condorcet

Paradoxe de Saint-Pétersbourg

Filtrage collaboratif

Théorie des jeux

Aversion au risque

fonction d'utilité

Bibliographie

Méthodologie Multicritère d'Aide à la Décision, Bernard Roy, Economica, 1985 (ISBN 2717809015 et ISBN 978-2717809015)

Aide multicritère à la décision, Bernard Roy et Denis Bouyssou, Economica, 1993 (ISBN 2717824731 et ISBN 978-2717824735)

L'aide multicritère à la décision, Philippe Vincke, Ellipse Marketing, 1998 (ISBN 2729889426 et ISBN 978-2729889425)

Risque et décision, Jean-Pascal Gayant, Vuibert, 2001 (ISBN 2-7117-7538-0)

Portail des probabilités et des statistiques

Ce document provient de « Th%C3%A9orie de la d%C3%A9cision ».

Catégories : Décision | Systémique | Statistiques

Contenu soumis à la licence CC-BY-SA. Source : Article Theorie de la decision de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Théorie de la décision — ● Théorie de la décision théorie fondée sur la prise en considération conjointe des probabilités et des utilités des diverses éventualités en vue de la prise de décision … Encyclopédie Universelle
Théorie de la décision — La théorie de la décision est une théorie de mathématiques appliquées ayant pour objet la prise de décision en univers risqué. Sommaire 1 Les limites de la théorie des probabilités 2 Risque ou incertitude ? 3 Gain non quantifiable … Wikipédia en Français
DÉCISION — La réflexion moderne sur la question de savoir quel parti prendre lorsqu’on se trouve confronté à un choix difficile a été esquissée pour la première fois par Blaise Pascal, au XVIIe siècle, dans le fameux texte du «pari» sur l’entrée dans la… … Encyclopédie Universelle
Theorie de l'information — Théorie de l information La théorie de l information, sans précision, est le nom usuel désignant la théorie de l information de Shannon, qui est une théorie probabiliste permettant de quantifier le contenu moyen en information d un ensemble de… … Wikipédia en Français
Théorie de l'Information — La théorie de l information, sans précision, est le nom usuel désignant la théorie de l information de Shannon, qui est une théorie probabiliste permettant de quantifier le contenu moyen en information d un ensemble de messages, dont le codage… … Wikipédia en Français
Theorie Dempster-Shafer — Théorie Dempster Shafer La Théorie Dempster Shafer est une théorie mathématique basée sur la notion de preuves[1] utilisant les fonctions de croyance et le raisonnement plausible. Le but de cette théorie est de permettre de combiner des preuves… … Wikipédia en Français
Théorie dempster-shafer — La Théorie Dempster Shafer est une théorie mathématique basée sur la notion de preuves[1] utilisant les fonctions de croyance et le raisonnement plausible. Le but de cette théorie est de permettre de combiner des preuves distinctes pour calculer… … Wikipédia en Français
Decision — Décision La décision est le fait d effectuer un choix lors de la confrontation à un problème afin de le résoudre. Il existe au moins trois grandes approches du concept de décision : La première estime que la décision est un choix de type… … Wikipédia en Français
Theorie de l'action — Théorie de l action La théorie de l action est l étude de la nature de l action humaine, qu elle soit individuelle ou collective. Les différentes disciplines qui s intéressent à la théorie de l action sont la philosophie de l action, la… … Wikipédia en Français
Décision — « Décidé » redirige ici. Pour le navire corsaire, voir Le Décidé. La décision est le fait d un acteur (ou d un ensemble plus ou moins cohérent d acteurs) qui effectue un choix entre plusieurs solutions susceptibles de résoudre le… … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts