Theoreme de recursion de Kleene

Theoreme de recursion de Kleene

Théorème de récursion de Kleene

Le théorème de récursion de Kleene est un théorème important de la théorie de la calculabilité. Il permet d'établir l'égalité de fonctions calculables.

Sommaire

Formulation avec les énumérations de fonctions récursives

Si 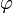\varphi{} est une enumération acceptable des fonctions recursives et f une fonction partielle récursive alors il existe un indice 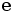{\mathbf{e}} tel que

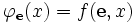\varphi_{\mathbf{e}}(x)=f(\mathbf{e},x).

  • Pour un langage de programmation

Si 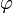\varphi{} est un langage de programmation acceptable et f une fonction semi-calculable alors il existe un programme 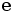{\mathbf{e}} tel que pour tout x

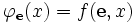\varphi_{\mathbf{e}}(x)=f(\mathbf{e},x).

Autre formes

Ce théorème peut être décliné sous différentes formes dont l'une des plus célèbre est dues à H. Rogers. On considère un langage de programmation acceptable \varphi.

  • Forme de Rogers

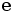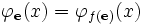Si f est une fonction calculable alors il existe un programme {\mathbf{e}} tel que pour tout x \varphi_{\mathbf{e}}(x)=\varphi_{f(\mathbf{e})}(x).

  • Paramétrisée

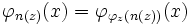Il existe une fonction calculable n telle que pour tout x et y. \varphi_{n(z)}(x)=\varphi_{\varphi_{z}(n(z))}(x).

  • Récursion double

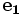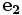Si f et g sont des fonctions calculables alors il existe deux programmes {\mathbf{e_1}} et {\mathbf{e_2}} tels que pour tout x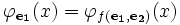

\varphi_{\mathbf{e_1}}(x)=\varphi_{f(\mathbf{e_1},\mathbf{e_2})}(x)

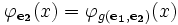\varphi_{\mathbf{e_2}}(x)=\varphi_{g(\mathbf{e_1},\mathbf{e_2})}(x).

On doit le théorème de récursion double à R.Smullyan.

Remarque

La démonstration de ce théorème utilise l'auto-référence s(x,x) produite par le théorème d'itération (théorème s-m-n). Cette notion d'autoréférence est très profonde et a été largement traitée par John von Neumann dans le cadre des automates cellulaires auto-reproducteurs.

Applications

Ce théorème est reconnu comme le meilleur outil permettant de produire contre-exemples et cas pathologiques. En particulier, il fournit l'existence de programmes calculant leurs propres codes. En prenant f la première projection, f(y,x) = y et en appliquant le théorème on obtient un programme 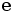{\mathbf{e}} tel que pour tout x

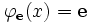\varphi_{\mathbf{e}}(x)=\mathbf{e}.

L'exécution du programme 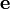\mathbf{e} produit son propre code. De tels programmes sont communément appelés quines.

  • Portail de l’informatique Portail de l’informatique
Ce document provient de « Th%C3%A9or%C3%A8me de r%C3%A9cursion de Kleene ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de recursion de Kleene de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Théorème de récursion de kleene — Le théorème de récursion de Kleene est un théorème important de la théorie de la calculabilité. Il permet d établir l égalité de fonctions calculables. Sommaire 1 Formulation avec les énumérations de fonctions récursives 2 Autre formes 3 …   Wikipédia en Français

  • Théorème de récursion de Kleene —  Ne doit pas être confondu avec Théorème de Kleene ni Théorème du point fixe de Kleene. En théorie de la calculabilité plusieurs théorèmes dus à à Kleene sont appelés théorèmes de la récursion. Ils établissent l existence de points fixes… …   Wikipédia en Français

  • Theoreme d'iteration — Théorème d itération Le théorème d itération est du à Stephen Kleene, il est aussi connu sous le nom de théorème s m n dans sa forme paramétrisée. Sommaire 1 Énoncé 1.1 Pour une énumération de fonction récursive 1.2 Pour un langage de programmat …   Wikipédia en Français

  • Théorème de Kleene —  Ne doit pas être confondu avec Théorème de récursion de Kleene ni Théorème du point fixe de Kleene. En informatique théorique, et plus précisément en théorie des automates, le théorème de Kleene affirme qu un langage peut être décrit par… …   Wikipédia en Français

  • Théorème du point fixe de Kleene —  Ne doit pas être confondu avec Théorème de Kleene ni Théorème de récursion de Kleene. En mathématiques, dans le domaine de la théorie des ordres, le théorème du point fixe de Kleene, s énonce comme suit : Soient L un ordre partiel… …   Wikipédia en Français

  • Kleene — Stephen Cole Kleene Stephen Cole Kleene (né le 5 janvier 1909 à Hartford, mort le 25 janvier 1994) est un mathématicien et logicien américain. Biographie et contribution scientifique Kleene est connu pour avoir fondé la branche de la logique… …   Wikipédia en Français

  • Théorème d'itération — Le théorème d itération est dû à Stephen Kleene, il est aussi connu sous le nom de théorème s m n dans sa forme paramétrisée. Sommaire 1 Énoncé 1.1 Pour une énumération de fonction récursive 1.2 Pour un langage de programmation …   Wikipédia en Français

  • Stephen Cole Kleene — Kleene en 1978 Stephen Cole Kleene – né le 5 janvier 1909 à Hartford (Connecticut) et mort le 25 janvier 1994 à Madison (Wisconsin) – est un mathématicien et logicien américain. Biographie et contribution scientifique Klee …   Wikipédia en Français

  • Théorie de la récursion — Calculabilité La théorie de la calculabilité (appelée aussi parfois théorie de la récursion) est une branche de la logique mathématique et de l informatique théorique. Alors que la notion intuitive de fonction calculable est aussi vieille que les …   Wikipédia en Français

  • Récursion Primitive — Fonction récursive primitive Une fonction récursive primitive est une fonction définie principalement à l aide de fonctions primitives de récursion et de composition. Ces fonctions constituent un sous ensemble des fonctions récursives. Elles ont… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”