Fonction Semi-Calculable

Fonction semi-calculable

En informatique théorique, les fonctions semi-calculables ou fonctions partielles récursives sont les fonctions calculables par les machines de Turing ou tout autre système de programmation Turing-complet.

En logique mathématique les fonctions semi-calculables correspondent aux relations fonctionnelles 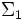$\Sigma_1~$ (Hiérarchie arithmétique).

Exemple

Les fonctions récursives peuvent être obtenues en ajoutant aux opérateurs permis dans la définition des fonctions récursives primitives le schéma µ, à savoir :

μ f (x 1,..., x n) = inf y {f (y, x 1,..., x n) = 0}

Autrement dit, $μ f (x 1,..., x n)$ calcule le plus petit y annulant $f (y, x 1,..., x n)$ . Si un tel y n'existe pas, le calcul de la fonction $μ$ ne se termine pas.

En termes plus intuitifs, cela revient à rajouter les boucles tant-que (while) dans un langage qui n'aurait que des boucles pour-tout bornées (for), le calcul de y pouvant être opéré comme suit :

y=0

while

f (y, x 1,..., x n)

<> 0 do y := y+1 od

return(y)

Portail de l’informatique

Ce document provient de « Fonction semi-calculable ».

Catégorie : Calculabilité

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction Semi-Calculable de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Fonction semi-calculable — En informatique théorique, les fonctions semi calculables ou fonctions partielles récursives sont les fonctions calculables par les machines de Turing ou tout autre système de programmation Turing complet. En logique mathématique les fonctions… … Wikipédia en Français
Fonction Calculable — Une fonction calculable (ou fonction récursive) est une fonction semi calculable (ou fonction partielle récursive) qui est aussi totale, c est à dire définie pour toute entrée (en tout point). Ce sont les fonctions calculées par une machine de… … Wikipédia en Français
Fonction calculable — Une fonction calculable (ou fonction récursive) est une fonction semi calculable (ou fonction partielle récursive) qui est aussi totale, c est à dire définie pour toute entrée (en tout point). Ce sont les fonctions calculées par une machine de… … Wikipédia en Français
Théorème de récursion de Kleene — Ne doit pas être confondu avec Théorème de Kleene ni Théorème du point fixe de Kleene. En théorie de la calculabilité plusieurs théorèmes dus à à Kleene sont appelés théorèmes de la récursion. Ils établissent l existence de points fixes… … Wikipédia en Français
Theoreme de recursion de Kleene — Théorème de récursion de Kleene Le théorème de récursion de Kleene est un théorème important de la théorie de la calculabilité. Il permet d établir l égalité de fonctions calculables. Sommaire 1 Formulation avec les énumérations de fonctions… … Wikipédia en Français
Théorème de récursion de kleene — Le théorème de récursion de Kleene est un théorème important de la théorie de la calculabilité. Il permet d établir l égalité de fonctions calculables. Sommaire 1 Formulation avec les énumérations de fonctions récursives 2 Autre formes 3 … Wikipédia en Français
LOGIQUE MATHÉMATIQUE — La logique au sens étroit du terme, c’est à dire la logique formelle par opposition à l’épistémologie ou à la théorie de la connaissance, se propose de donner une théorie de l’inférence formellement valide. Elle considère comme valide toute… … Encyclopédie Universelle
RÉCURSIVITÉ — Les (semi ) fonctions récursives ont été introduites pour donner un équivalent mathématique à la notion métamathématique intuitive de (semi ) fonction effectivement ou mécaniquement calculable (cf. LOGIQUE MATHÉMATIQUE, chap. 4). Par souci de… … Encyclopédie Universelle
Thèse de Church — La thèse de Church du nom du mathématicien Alonzo Church est une hypothèse ( thèse ) concernant la définition de la notion de calculabilité. Dans une forme dite physique [1], elle affirme que la notion physique de la calculabilité, définie comme… … Wikipédia en Français
These de Church — Thèse de Church La thèse de Church du nom du mathématicien Alonzo Church est le principe de base de la calculabilité. Dans sa forme la plus ordinaire, elle affirme que tout traitement réalisable mécaniquement peut être accompli par un ordinateur… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction Semi-Calculable