Theoreme d'iteration

Theoreme d'iteration

Théorème d'itération

Le théorème d'itération est du à Stephen Kleene, il est aussi connu sous le nom de théorème s-m-n dans sa forme paramétrisée.

Sommaire

Énoncé

Pour une énumération de fonction récursive

Si 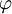\varphi~ est une enumération acceptable, alors il existe une fonction partielle récursive 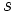s~ telle que pour tout indice 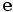\mathbf{e}~ et tous nombres 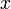x~ et y~

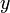
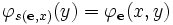\varphi_{s(\mathbf{e},x)}(y)=\varphi_{\mathbf{e}}(x,y).

Pour un langage de programmation

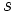Si \varphi est un langage de programmation acceptable alors il existe une fonction calculable s~ telle que pour tout programme 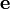\mathbf{e} et tous 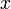x~ et y~

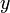
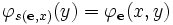\varphi_{s(\mathbf{e},x)}(y)=\varphi_{\mathbf{e}}(x,y).

s est appelée fonction d'itération ou fonction s-m-n dans sa forme paramétrisée.

Évaluation partielle

La fonction d'itération est un des points fondamentaux de l'évaluation partielle. En effet, dans 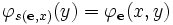\varphi_{s(\mathbf{e},x)}(y)=\varphi_{\mathbf{e}}(x,y), le programme 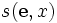s(\mathbf{e},x) peut être vue comme la spécialisation du programme 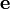\mathbf{e} pour l'entrée 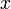x~, en d'autres termes, le programme 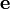\mathbf{e} dont la première entrée a été fixée pour la valeur 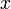x~. Pour cette notion, on pourra se réferrer aux travaux de N. Jones.

Auto-référence

Par 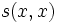s(x,x)~, ce théorème permet de construire des programmes faisant référence à leurs propres codes puisque 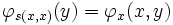\varphi_{s(x,x)}(y)=\varphi_{x}(x,y). En particulier, 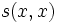s(x,x)~ est fondamental dans la construction d'une machine de Turing dont l'arrêt est indécidable ou dans la preuve du théorème de récursion de Kleene.

  • Portail de l’informatique Portail de l’informatique
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me d%27it%C3%A9ration ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme d'iteration de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Théorème d'itération — Le théorème d itération est dû à Stephen Kleene, il est aussi connu sous le nom de théorème s m n dans sa forme paramétrisée. Sommaire 1 Énoncé 1.1 Pour une énumération de fonction récursive 1.2 Pour un langage de programmation …   Wikipédia en Français

  • Theoreme de recursion de Kleene — Théorème de récursion de Kleene Le théorème de récursion de Kleene est un théorème important de la théorie de la calculabilité. Il permet d établir l égalité de fonctions calculables. Sommaire 1 Formulation avec les énumérations de fonctions… …   Wikipédia en Français

  • Théorème de récursion de kleene — Le théorème de récursion de Kleene est un théorème important de la théorie de la calculabilité. Il permet d établir l égalité de fonctions calculables. Sommaire 1 Formulation avec les énumérations de fonctions récursives 2 Autre formes 3 …   Wikipédia en Français

  • Théorème de récursion de Kleene —  Ne doit pas être confondu avec Théorème de Kleene ni Théorème du point fixe de Kleene. En théorie de la calculabilité plusieurs théorèmes dus à à Kleene sont appelés théorèmes de la récursion. Ils établissent l existence de points fixes… …   Wikipédia en Français

  • Theoreme d'inversion locale — Théorème d inversion locale En mathématiques, le théorème d inversion locale est un résultat de géométrie différentielle. Il indique que si une fonction f est continûment différentiable en un point a, si cette différentielle est une bijection… …   Wikipédia en Français

  • Theoreme de completude de Godel — Théorème de complétude de Gödel Le théorème de complétude du calcul des prédicats du premier ordre a été démontré par Kurt Gödel (1929, thèse de doctorat, sur la complétude du calcul logique). Il affirme que le calcul des prédicats est complet au …   Wikipédia en Français

  • Théorème de complétude — de Gödel Le théorème de complétude du calcul des prédicats du premier ordre a été démontré par Kurt Gödel (1929, thèse de doctorat, sur la complétude du calcul logique). Il affirme que le calcul des prédicats est complet au sens où toute… …   Wikipédia en Français

  • Théorème de complétude de gödel — Le théorème de complétude du calcul des prédicats du premier ordre a été démontré par Kurt Gödel (1929, thèse de doctorat, sur la complétude du calcul logique). Il affirme que le calcul des prédicats est complet au sens où toute proposition qui… …   Wikipédia en Français

  • Theoreme des valeurs intermediaires — Théorème des valeurs intermédiaires Pour les articles homonymes, voir TVI. Le théorème des valeurs intermédiaires (TVI) est un théorème important en analyse et concerne des fonctions continues sur un intervalle. Il indique que si une fonction… …   Wikipédia en Français

  • Théorème de Bolzano — Théorème des valeurs intermédiaires Pour les articles homonymes, voir TVI. Le théorème des valeurs intermédiaires (TVI) est un théorème important en analyse et concerne des fonctions continues sur un intervalle. Il indique que si une fonction… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”