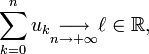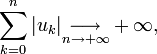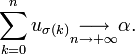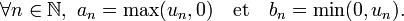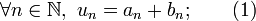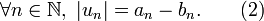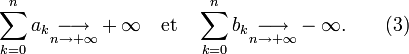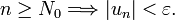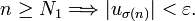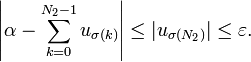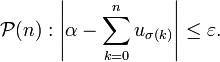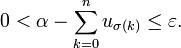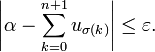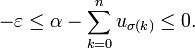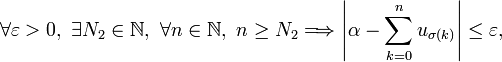Theoreme de rearrangement de Riemann

Théorème de réarrangement de Riemann

En mathématiques, le théorème de réarrangement de Riemann est un théorème, nommé en l'honneur du mathématicien Bernhard Riemann, d'après lequel si une série à valeurs réelles est semi-convergente, alors on peut réarranger ses termes pour qu'elle converge vers n'importe quel réel, et même tendre vers plus ou moins l'infini.

Sommaire

1 Énoncé
2 Démonstration
- 2.1 Lemme
- 2.2 Démonstration principale
  - 2.2.1 Construction de la permutation
  - 2.2.2 Convergence
3 Références

Énoncé

Soit 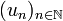$(u_n)_{n \in \N}$ une suite à valeurs réelles telle que sa série associée soit semi-convergente, c'est-à-dire que

$\sum_{k=0}^n u_k \underset{n \rightarrow +\infty}{\longrightarrow} \ell \in \R,$

mais

$\sum_{k=0}^n |u_k| \underset{n \rightarrow +\infty}{\longrightarrow} + \infty,$

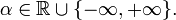
Et soit $\alpha \in \R \cup \{-\infty,+\infty\}.$

Alors il existe une permutation $σ$ de 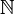$\N$ tel que

$\sum_{k=0}^n u_{\sigma(k)} \underset{n \rightarrow +\infty}{\longrightarrow} \alpha.$

Démonstration

Lemme

Posons

$\forall n \in \N,\ a_n=\max(u_n,0) \quad \text{et} \quad b_n=\min(0,u_n).$

On a alors

$\forall n \in \N,\ u_n=a_n+b_n; \qquad (1)$

$\forall n \in \N,\ |u_n|=a_n-b_n. \qquad (2)$

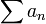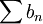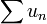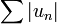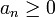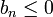Les séries $\sum a_n$ et $\sum b_n$ convergent ou divergent simultanément d'après (1) car la série $\sum u_n$ converge. Mais si les deux convergent, cela implique d'après (2) que la série $\sum |u_n|$ converge, ce qui est absurde. Finalement, comme $a_n \geq 0$ et $b_n \leq 0$ pour tout 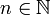$n \in \N$ , on a

$\sum_{k=0}^n a_k \underset{n \rightarrow +\infty}{\longrightarrow} +\infty \quad \text{et} \quad \sum_{k=0}^n b_k \underset{n \rightarrow +\infty}{\longrightarrow} -\infty.\qquad (3)$

Démonstration principale

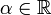On suppose ici que $\alpha\in \R$ .

Construction de la permutation

On construit une permutation $σ$ de 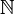$\N$ de la façon suivante. On commence à sommer les termes positifs (sans en omettre) ou nuls jusqu'à dépasser $α$ (possible d'après (3)). Puis on somme tous les termes strictement négatifs jusqu'à ce que la somme partielle soit strictement inférieure à $α$ (possible d'après (3)). Puis on itère le procédé, en sommant les termes positifs à partir de là on s'était arrêté, puis les termes négatifs, etc... On a bien construit une permutation.

Convergence

Soit 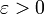$\varepsilon>0$ . Il existe 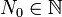$N_0\in \N$ tel que pour tout $n \in \N$ ,

$n\geq N_0 \Longrightarrow |u_n|<\varepsilon.$

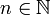Sinon la série serait grossièrement divergente. Il existe donc 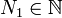$N_1\in\N$ tel que pour tout $n \in \N$ ,

$n\geq N_1 \Longrightarrow |u_{\sigma(n)}|<\varepsilon.$

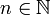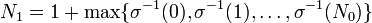Par exemple, il suffit de prendre $N_1=1+\max\{\sigma^{-1}(0),\sigma^{-1}(1),\ldots,\sigma^{-1}(N_0)\}$ .

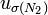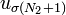Soit maintenant $N 2$ le plus petit entier strictement supérieur à $N 1$ tel que $u_{\sigma(N_2)}$ et $u_{\sigma(N_2+1)}$ soient de signes opposés. On a alors

$\left|\alpha-\sum_{k=0}^{N_2-1} u_{\sigma(k)} \right| \leq | u_{\sigma(N_2)}|\leq \varepsilon.$

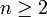Pour $n \geq 2$ , on pose alors la proposition

$\mathcal{P}(n): \left|\alpha-\sum_{k=0}^{n} u_{\sigma(k)} \right| \leq \varepsilon.$

On a vu que 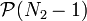$\mathcal{P}(N_2-1)$ est vraie. Supposons alors que pour 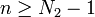$n \geq N_2-1$ , la proposition 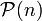$\mathcal{P}(n)$ soit vraie. Distinguons alors deux cas:

Premier cas, on a

$0<\alpha-\sum_{k=0}^{n} u_{\sigma(k)}\leq \varepsilon.$

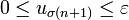Alors $0 \leq u_{\sigma(n+1)} \leq \varepsilon$ donc

$\left|\alpha-\sum_{k=0}^{n+1} u_{\sigma(k)} \right| \leq \varepsilon.$

Deuxième cas, on a

$-\varepsilon \leq \alpha-\sum_{k=0}^{n} u_{\sigma(k)}\leq 0.$

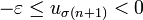Alors $-\varepsilon \leq u_{\sigma(n+1)} < 0$ donc

$\left|\alpha-\sum_{k=0}^{n+1} u_{\sigma(k)} \right| \leq \varepsilon.$

Finalement par principe de récurrence, on a montré que

$\forall \varepsilon>0,\ \exists N_2 \in \N,\ \forall n \in \N,\ n \geq N_2 \Longrightarrow \left|\alpha-\sum_{k=0}^{n} u_{\sigma(k)} \right| \leq \varepsilon,$

ce qui achève la preuve.

Références

L'article de Bernhard Riemann Histoire des recherches relatives à la représentation par une série trigonomètrique d'une fonction donnée arbitrairement dans l'ouvrage Et Dieu créa les nombres, les plus grands textes de mathématiques réunis et commentés par Stephen Hawking chez Dunod.

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de r%C3%A9arrangement de Riemann ».

Catégories : Série | Bernhard Riemann | Théorème de mathématiques | Permutation

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de rearrangement de Riemann de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Théorème de réarrangement de Riemann — En mathématiques, le théorème de réarrangement de Riemann est un théorème, nommé en l honneur du mathématicien Bernhard Riemann, d après lequel si une série à valeurs réelles est semi convergente, alors on peut réarranger ses termes pour qu elle… … Wikipédia en Français
Bernhard Riemann — Pour les articles homonymes, voir Riemann. Bernhard Riemann Bernhard Riemann Naissance 17 … Wikipédia en Français
Bernard Riemann — Bernhard Riemann Pour les articles homonymes, voir Riemann. Bernhard Riemann Bernhard Riemann … Wikipédia en Français
Georg Friedrich Bernhard Riemann — Bernhard Riemann Pour les articles homonymes, voir Riemann. Bernhard Riemann Bernhard Riemann … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Permutable — Permutation En mathématiques, la notion de permutation exprime l idée de réarrangement d objets discernables. Une permutation de n objets distincts rangés dans un certain ordre, correspond à un changement de l ordre de succession de ces n objets … Wikipédia en Français
Permutation — En mathématiques, la notion de permutation exprime l idée de réarrangement d objets discernables. Une permutation de n objets distincts rangés dans un certain ordre, correspond à un changement de l ordre de succession de ces n objets. La… … Wikipédia en Français
Convergence Absolue — En mathématiques, on dit qu une série numérique converge absolument lorsque la série des valeurs absolues (ou des modules) est convergente. C est une condition suffisante très utile de convergence pour la série elle même. Cette condition… … Wikipédia en Français
Convergence absolue — Pour les articles homonymes, voir Absolu. En mathématiques, une série numérique réelle ou complexe converge absolument si, par définition, la série des valeurs absolues (ou des modules) est convergente. Cette définition peut être étendue aux… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Theoreme de rearrangement de Riemann

Théorème de réarrangement de Riemann

Sommaire

Énoncé