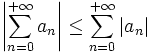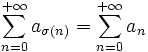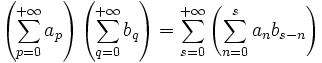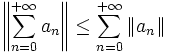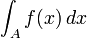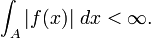Semi-convergence

Semi-convergence

Convergence absolue

En mathématiques, on dit qu'une série numérique 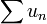\sum u_n converge absolument lorsque la série des valeurs absolues (ou des modules) 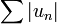\sum |u_n| est convergente. C'est une condition suffisante très utile de convergence pour la série 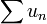\sum u_n elle-même. Cette condition suffisante peut être étendue aux séries à valeurs dans un espace vectoriel normé complet.

De façon symétrique, on dit qu'une intégrale converge absolument si l'intégrale de la valeur absolue (du module ou de la norme) de l'intégrande est convergente.

L'absolue convergence des séries ou des intégrales est étroitement liée à la sommabilité (des familles ou des fonctions), et apporte des propriétés plus fortes que la convergence.

Sommaire

Série numérique absolument convergente

Une série à termes réels ou complexes 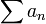\sum a_n converge absolument quand la série de terme général | an | converge. Dans ce cas, la série 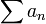\sum a_n converge elle aussi et l'inégalité triangulaire se généralise en

\left|\sum_{n=0}^{+\infty} a_n \right|\leq \sum_{n=0}^{+\infty} |a_n|

Si la série est convergente, mais non absolument convergente, elle est dite semi-convergente.

Exemple : la série harmonique alternée 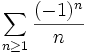\sum_{n\ge 1}\frac{(-1)^n}{n} est semi-convergente.

Comportement des séries à termes réels

Dans le cas où on a affaire à une série de réels, le théorème précédent possède une démonstration élémentaire, qui apporte des informations supplémentaires sur les comportements possibles.

Si les termes an de la série sont des réels, on peut séparer les termes positifs et négatifs. Il faut considérer pour cela les termes 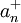a_n^+ partie positive et 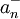a_n^- partie négative du terme an

a_n^+=\max(a_n,0)\qquad a_n^-=\max(-a_n,0)

Ces deux termes sont positifs, l'un est nul, et l'autre égal à la valeur absolue de an. De sorte que

a_n = a_n^+-a_n^- \qquad |a_n| = a_n^++a_n^-

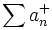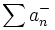Les séries \sum a_n^+ et \sum a_n^- étant à termes positifs, leur suite des sommes partielles est croissante ; elle converge ou tend vers l'infini. Convergence absolue et semi-convergence peuvent être formulées à l'aide de ces deux séries.

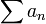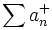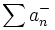  • Lorsque la série \sum a_n converge absolument, par comparaison de séries positives, les séries \sum a_n^+ et \sum a_n^- convergent toutes deux, donc par linéarité la série 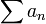\sum a_n aussi.
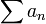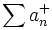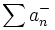  • Lorsque la série \sum a_n est semi-convergente, nécessairement les deux séries \sum a_n^+ et \sum a_n^- divergent (chacune a une somme infinie). La convergence se fait donc par compensation entre les termes positifs et négatifs.

La propriété « absolue convergence implique convergence » peut ensuite être étendue aux séries à valeurs complexes en séparant de la même façon parties réelle et imaginaire.

Propriétés des séries absolument convergentes

Si une série est absolument convergente, elle jouit de propriétés particulières, valables pour les sommes finies, mais fausses pour les séries en général

  • généralisation de la commutativité : la convergence et la valeur de la somme ne dépendent pas de l'ordre des termes. Ainsi, si σ est une permutation de 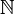{\mathbb N}, il est possible d'écrire
\sum_{n=0}^{+\infty} a_{\sigma(n)}= \sum_{n=0}^{+\infty} a_n

Si la série est au contraire semi-convergente un théorème de Riemann montre que changer l'ordre des termes peut conduire à une série divergente, ou à une série convergente de somme arbitrairement choisie.

\left(\sum_{p=0}^{+\infty} a_p\right)\left(\sum_{q=0}^{+\infty} b_q\right)= \sum_{s=0}^{+\infty} \left(\sum_{n=0}^s a_nb_{s-n}\right)

Une autre façon d'obtenir ces propriétés pour des sommes infinies est de considérer la notion de famille sommable, très voisine de la propriété d'absolue convergence pour les séries numériques.

Extension aux séries à valeurs vectorielles

Le cadre est cette fois un espace vectoriel normé E. Une série à termes vectoriels 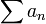\sum a_n converge absolument quand la série de terme général 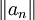\| a_n \| converge.

Lorsque l'espace vectoriel E est complet, la convergence absolue fournit encore une condition suffisante de convergence : si la série converge absolument, elle converge et

\left\|\sum_{n=0}^{+\infty} a_n \right\|\leq \sum_{n=0}^{+\infty} \|a_n\|

Cette propriété se prouve en utilisant le critère de Cauchy pour caractériser ces convergences.

Il s'agit en fait d'une équivalence : si E est un espace vectoriel normé tel que toute série absolument convergente converge, alors E est complet.

Intégrale absolument convergente

De même, une intégrale:

\int_A f(x)\,dx

converge absolument si l'intégrale de sa valeur absolue correspondante est finie:

\int_A \left|f(x)\right|\,dx<\infty.

Articles connexes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Convergence absolue ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Semi-convergence de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Convergence Absolue — En mathématiques, on dit qu une série numérique converge absolument lorsque la série des valeurs absolues (ou des modules) est convergente. C est une condition suffisante très utile de convergence pour la série elle même. Cette condition… …   Wikipédia en Français

  • Convergence absolue — Pour les articles homonymes, voir Absolu. En mathématiques, une série numérique réelle ou complexe converge absolument si, par définition, la série des valeurs absolues (ou des modules) est convergente. Cette définition peut être étendue aux… …   Wikipédia en Français

  • Convergence of random variables — In probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to …   Wikipedia

  • Convergence of measures — In mathematics, more specifically measure theory, there are various notions of the convergence of measures. Three of the most common notions of convergence are described below. Contents 1 Total variation convergence of measures 2 Strong… …   Wikipedia

  • Convergence faible — Topologie faible En mathématiques, la topologie faible d un espace vectoriel topologique E est une topologie définie sur E au moyen de son dual topologique E . On définit également sur E une topologie dite faible * au moyen de E. Sommaire 1… …   Wikipédia en Français

  • Série semi-convergente — Série (mathématiques) Pour les articles homonymes, voir Série. En mathématiques, la série constitue une généralisation de la notion de somme, pour une succession infinie de termes. L étude des séries consiste à effectuer la somme d un nombre fini …   Wikipédia en Français

  • Anticyclone semi-permanent — Anticyclone Pour les articles homonymes, voir Anticyclone (homonymie). Un anticyclone est une zone de circulation atmosphérique autour d un centre de haute pression. Leur sens de rotation est lié à la force de Coriolis: ils tournent dans le sens… …   Wikipédia en Français

  • ÉCONOMIE MONDIALE - 1996 , sur la voie de la convergence — Consolidation, ajustement et amorce de convergence ont, en 1996, caractérisé la conjoncture dans la plupart des régions du monde. L’activité s’est en effet sensiblement raffermie, après la pause de l’année précédente, et les promesses d’une… …   Encyclopédie Universelle

  • Series (mathematics) — A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely.[1] In mathematics, given an infinite sequence of numbers { an } …   Wikipedia

  • SÉRIES ET PRODUITS INFINIS — La notion de limite d’une suite est à la base de l’analyse. Le langage des séries, équivalent à celui des suites, s’est imposé dès le XVIIe siècle à propos du développement des fonctions en série entière. Cependant, les fondements rigoureux de la …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”