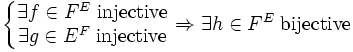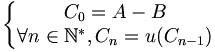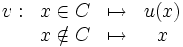Théorème de Schröder-Bernstein

Théorème de Schröder-Bernstein

Théorème de Cantor-Bernstein

Le théorème de Cantor-Bernstein, également appelé théorème de Cantor-Schröder-Bernstein, est un théorème de la théorie des ensembles. Il est nommé en l'honneur des mathématiciens Georg Cantor, Felix Bernstein et Ernst Schröder. Cantor en donna une première démonstration, mais qui utilisait implicitement l'axiome du choix. Bernstein et Schröder en donnèrent des démonstrations qui ne dépendaient pas de cet axiome.

Sommaire

Historique

Georg Cantor l'énonce dans son livre Sur les fondements de la théorie des ensembles transfinis mais ne le démontre pas. Felix Bernstein, élève de celui-ci en esquisse une démonstration dès 1896 à l'âge de 18 ans. Elle est publiée en 1898 sur proposition de Cantor dans Leçons sur la théorie des fonctions sous la plume d'Émile Borel. Ernst Schröder le démontre également dans un article daté de la même année, cette démonstration étant cependant considérée comme imparfaite[1].

Richard Dedekind en fit lui même une démonstration en 1897 mais qui ne fut publiée qu'en 1930. Ernst Zermelo en fait une autre en 1906 qui reprend en fait les idées de Dedekind

Énoncé

S'il existe une injection f d'un ensemble E vers un ensemble F, et une injection g de l'ensemble F vers l'ensemble E, alors il existe une bijection h de E sur F.

\left\{\begin{matrix}\exist f \in F^E \;{\rm injective} \\ \exist g \in E^F \;{\rm injective} \end{matrix} \right. \Rightarrow \exist h \in F^E \;{\rm bijective}

Démonstration n°1

Lemme préliminaire

Commençons par montrer que si u est une application injective d'un ensemble A vers un ensemble B avec 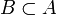B \subset A, alors il existe une bijection v de A sur B.

Théorème de Cantor-Bernstein.

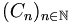Soit (C_n)_{n \in \mathbb N} la suite définie par :

\left\{\begin{matrix} C_0 = A - B \\ \forall n \in \mathbb{N}^*, C_n = u( C_{n-1} ) \end{matrix} \right.

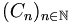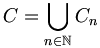
Soit C la réunion de tous les ensembles (C_n)_{n \in \mathbb N} : C=\bigcup_{n \in \mathbb N}C_n

Soit alors v l'application de A dans B défini par :

\begin{matrix}v: & x \in C & \mapsto & u(x)\\ & x \notin C& \mapsto & x \end{matrix}

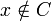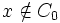v est bien défini à valeurs dans B, car u est à valeur dans B, et si x \notin C alors x \notin C_0 et donc x \in B.

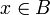Montrons que v est injective. Soient alors x et y deux éléments de A tel que v(x) = v(y)

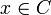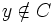  • Supposons que x \in C et y \notin C.
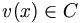Alors v(x) \in C (car C est stable par v) et 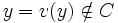y=v(y) \notin C. Or v(x) = v(y) ce qui est absurde.
  • Supposons que 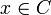x \in C et y \in C.
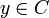Alors v(x) = u(x) = v(y) = u(y). Comme u est injective x = y.
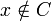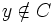  • Supposons que x \notin C et y \notin C.
Alors x = y = v(x) = v(y)
Dans tous les cas x = y, donc v est injective.

Montrons que v est surjective. Soit 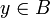y \in B. Montrons qu'il existe un 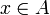x \in A tel que v(x) = y.

  • Si y \in C
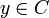
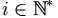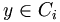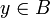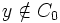alors il existe i \in \mathbb{N}^* tel que y \in C_i. (i est strictement positif car y \in B, donc y \notin C_0).
Il existe donc 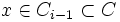x \in C_{i-1} \subset C tel que u(x) = v(x) = y.
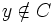
  • Si y \notin C
alors v(y) = y

Donc v est bijective. Ce qui démontre la première proposition.

Interprétation

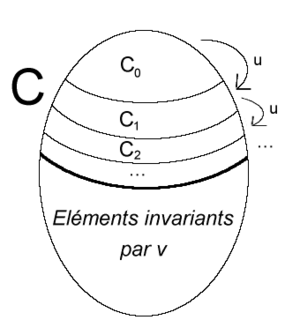
On peut donner une interprétation concrète du résultat montré ci-dessus. A est l'ensemble (infini !!) des spectateurs d'un théâtre (infini). Chaque spectateur a réservé une place, et initialement, on suppose que chaque place est occupée par un spectateur, mais pas forcément par le spectateur qui a réservé cette place. B est alors l'ensemble des spectateurs assis. Par ailleurs, les ensembles étant infinis, il peut rester des spectateurs debout. L'application u est l'application qui, à un spectateur x associe le spectateur y = u(x) assis à la place de x.

C0 est l'ensemble des spectateurs initialement debout. Ces spectateurs se rendent à leur place et délogent leur occupant. Ceux-ci forment alors l'ensemble C1. Ces derniers procèdent de même. Cn désigne les spectateurs debout à la n-ème étape. Ils vont aux places qu'ils ont réservé et en chassent leurs occupants. On itère une infinité de fois. C désigne l'ensemble des spectateurs qui se sont levés au moins une fois (y compris ceux qui étaient debout initialement).

L'application v désigne l'application, qui, à un spectateur x qui doit se lever, associe le spectateur y qu'il va déloger, ou bien qui, à un spectateur x qui reste toujours assis, associe x lui-même. L'application réciproque de v est l'application, qui, à un spectateur y qui est dérangé, associe le spectateur x qui vient prendre sa place, ou bien qui, à un spectateur y jamais dérangé, associe y lui-même.

Démonstration finale du théorème

Montrons alors le théorème initial.

Soit B = g(F) l'image de F par l'application g injective. L'application 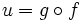u= g \circ f est une application injective de E dans B, avec 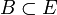B \subset E. Donc il existe une application bijective v de E sur B. Comme g est une injection, la restriction de g à son image pour espace d'arrivée est une bijection de F sur B. Donc la composée 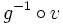g^{-1} \circ v est une bijection de E sur F, ce qui démontre le théorème de Cantor-Bernstein.

Démonstration n°2

Un lemme préliminaire

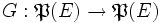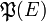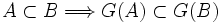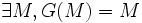Cette démonstration repose sur le lemme suivant, cas particulier du théorème de Knaster-Tarski. Soit E un ensemble et G : \mathfrak P(E) \to \mathfrak P(E) (où \mathfrak P(E) est l'ensemble des parties de E) une application croissante, i.e. A \subset B \Longrightarrow G(A) \subset G(B). Alors G admet un point fixe, i.e. \exists M, G(M) = M.

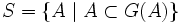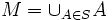En effet, posons S = \{A \;|\; A \subset G(A)\} et M = \cup_{A \in S} A. Alors :

  • pour tout 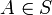A \in S, d'une part 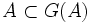A \subset G(A), d'autre part 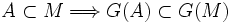A \subset M \Longrightarrow G(A) \subset G(M) car G est croissante. Donc 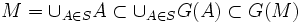M = \cup_{A \in S} A \subset \cup_{A \in S} G(A) \subset G(M) et donc 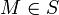M \in S. M est donc la partie maximale de S
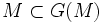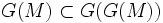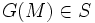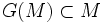  • M \subset G(M) donc G(M) \subset G(G(M)) car G est croissante. Donc G(M) \in S donc G(M) \subset M compte tenu de la maximalité de M comme élément de S. On a donc bien G(M) = M

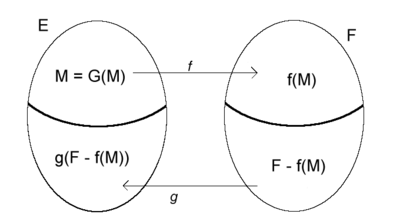
Démonstration finale

Soient maintenant f injective de E dans F et g injective de F dans E. Pour toute partie A de E, on pose G(A) = E − g(F − f(A)). On calcule f(A) ensemble des images des éléments de A par f, on en prend le complémentaire dans F, on prend l'ensemble g(F − f(A)) des images des éléments de cette partie par g et on prend le complémentaire dans E. Il n'est pas difficile de vérifier que G est croissante.

On introduit alors la partie M du lemme préliminaire. Cette partie est invariante par G ce qui signifie que g(F − f(M)) est exactement le complémentaire de M dans E.

Théorème de Cantor-Bernstein.

On pose :

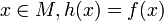
si x \in M, h(x) = f(x)
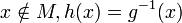
si x \notin M, h(x) = g^{-1}(x)

h est bijective de E dans F.

M joue un rôle comparable à la partie C dans la première démonstration ou à 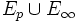E_p \cup E_{\infty} dans la démonstration qui suit.

Démonstration n° 3

Appelons ancêtres d'un élément x de E l'antécédent de x par g (s'il existe) puis l'antécédent de cet antécédent par f, etc. Procédons de même pour les éléments de F.

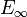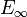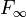Notons Ep (resp. Ei) l'ensemble des éléments de E ayant un nombre pair (resp. impair) d'ancêtres. Ep n'est autre que la partie C de la première démonstration. Notons E_\infty l'ensemble des éléments de E ayant un nombre infini d'ancêtres. Ep, Ei et E_\infty forment une partition de E. Définissons de même Fp, Fi et F_\infty.

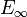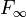f est une bijection de Ep sur Fi et aussi de E_\infty sur F_\infty. g est une bijection de Fp sur Ei, et sa réciproque est donc une bijection de Ei sur Fp.

Théorème de Cantor-Bernstein.

On peut ainsi construire une bijection de E sur F.

Applications

Si l'on considère la technique naïve qu'a un enfant pour compter le nombre d'éléments d'un ensemble, cela revient quasiment toujours à associer chacun des élements à un autre d'un ensemble connu dont le nombre d'éléments est connu.

Il peut s'agir soit d'associer chacun des éléments à compter avec l'un des doigts, soit d'associer chacun des éléments avec un nombre que l'on réciterait à haute voix (un, deux, trois, etc.), par exemple.

En clair, compter se fait naïvement en effectuant une bijection d'un ensemble dont la « dimension » est connue vers un autre dont la dimension est inconnue.

Ce théorème s'interprète alors comme disant : « Si je peux compter une partie d'un ensemble avec la totalité des éléments d'un autre ensemble, et réciproquement, alors ils ont le même nombre d'éléments ». Ce qui est évident pour des ensembles finis. Ce théorème généralise alors cette notion pour des ensembles infinis.

Si je peux compter un certain nombre de billes de mon sac de billes avec mes dix doigts, et qu'avec la totalité de mes billes, je peux les associer avec certains de mes doigts, alors j'ai exactement dix billes.

À partir de là, ce théorème représente l'une des briques de base pour généraliser la notion de tailles d'ensembles à des ensembles infinis.

Généralisation

Soient X un ensemble non vide et 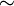\sim une relation d'équivalence sur l'ensemble des parties de X. On suppose qu'elle vérifie les deux propriétés:

  • si 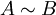\ A \sim B alors il existe une bijection f de A dans B telle que, pour tout sous-ensemble C de A, 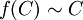\ f(C) \sim C;
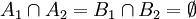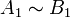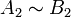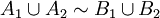  • si A_{1} \cap A_{2}=B_{1} \cap B_{2}=\emptyset et \ A_{1} \sim B_{1} et \ A_{2} \sim B_{2} alors A_{1} \cup A_{2} \sim B_{1} \cup B_{2}.

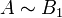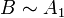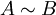Soient deux ensembles A et B, un sous-ensemble A1 de A et un sous-ensemble B1 de B. On suppose que \ A \sim B_{1} et \ B \sim A_{1}. Alors \ A \sim B.

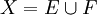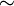Ceci peut également être démontré sans l'axiome du choix[2]. Dans le cas particulier où X=E \cup F et \sim est la relation d'équipotence, on retrouve le résultat précédent.

Références

  1. ↑ Casiro F, Le Théorème de Cantor-Bernstein, Tangente, mai-juin 2008, p42-44
  2. ↑ Stan WAGON, The Banach-Tarski Paradox, Editions Cambridge University Press, ISBN 0-521-45704-1
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Cantor-Bernstein ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Schröder-Bernstein de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Theoreme de Cantor-Bernstein — Théorème de Cantor Bernstein Le théorème de Cantor Bernstein, également appelé théorème de Cantor Schröder Bernstein, est un théorème de la théorie des ensembles. Il est nommé en l honneur des mathématiciens Georg Cantor, Felix Bernstein et Ernst …   Wikipédia en Français

  • Théorème de cantor-bernstein — Le théorème de Cantor Bernstein, également appelé théorème de Cantor Schröder Bernstein, est un théorème de la théorie des ensembles. Il est nommé en l honneur des mathématiciens Georg Cantor, Felix Bernstein et Ernst Schröder. Cantor en donna… …   Wikipédia en Français

  • Théorème de Cantor-Bernstein — Pour les articles homonymes, voir Théorème de Bernstein. Le théorème de Cantor Bernstein, également appelé théorème de Cantor Schröder Bernstein, est un théorème de la théorie des ensembles. Il est nommé en l honneur des mathématiciens Georg… …   Wikipédia en Français

  • Théorème de Cantor-Schröder-Bernstein — Théorème de Cantor Bernstein Le théorème de Cantor Bernstein, également appelé théorème de Cantor Schröder Bernstein, est un théorème de la théorie des ensembles. Il est nommé en l honneur des mathématiciens Georg Cantor, Felix Bernstein et Ernst …   Wikipédia en Français

  • Theoreme de Knaster-Tarski — Théorème de Knaster Tarski Le théorème de Knaster Tarski est un théorème de point fixe pour une application monotone d un treillis complet dans lui même ; aussi est il encore appelé théorème de point fixe de Knaster Tarski ou tout simplement …   Wikipédia en Français

  • Théorème de knaster-tarski — Le théorème de Knaster Tarski est un théorème de point fixe pour une application monotone d un treillis complet dans lui même ; aussi est il encore appelé théorème de point fixe de Knaster Tarski ou tout simplement de Tarski, le théorème… …   Wikipédia en Français

  • Théorème de Knaster-Tarski — Bronisław Knaster Alfred Tarski Le théorème de …   Wikipédia en Français

  • Ernst Schroder — Ernst Schröder Pour les articles homonymes, voir Schröder. Ernst Schröder Ernst Schröder (25 novembre  …   Wikipédia en Français

  • Ernst Schröder — Pour les articles homonymes, voir Schröder. Ernst Schröder Ernst Schröder (25 novembre 1841 à Mannheim – 16 juin 1902 à Karlsruhe) est un mathématicie …   Wikipédia en Français

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”