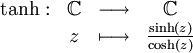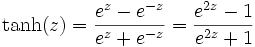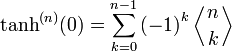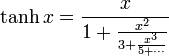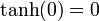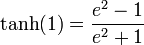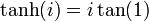Tanh

Tangente hyperbolique

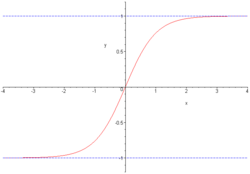
Graphe de la fonction tangente hyperbolique sur une partie de R

La tangente hyperbolique est, en mathématiques, une fonction hyperbolique.

Sommaire

1 Définition
2 Propriétés
3 Valeurs
4 Fonction réciproque
5 Voir aussi

Définition

La fonction tangente hyperbolique, notée tanh ou th est la fonction complexe suivante :

$\begin{matrix} \tanh: &\mathbb C &\longrightarrow &\mathbb C \\ \ &z &\longmapsto &\frac {\sinh(z)} {\cosh(z)} \end{matrix}$

où $s i n h$ est la fonction sinus hyperbolique et $c o s h$ la fonction cosinus hyperbolique. Cette définition est analogue à celle de la fonction tangente comme rapport du sinus et du cosinus.

La tangente hyperbolique peut s'exprimer à l'aide de la fonction exponentielle :

$\tanh(z)=\frac {e^z-e^{-z}} {e^z+e^{-z}} = \frac {e^{2z}-1} {e^{2z}+1}$

Propriétés

Propriétés générales

tanh est continue et infiniment dérivable.
C'est une fonction impaire.
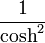La dérivée de tanh est $\frac {1} {\cosh^2}$ .
La primitive de tanh est 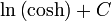$\ln \left(\cosh \right) + C$ , à une constante d'intégration C près.
La restriction de tanh à $\mathbb R$ est impaire et strictement croissante. Il s'agit d'une bijection de $\mathbb R$ dans $\left] -1; 1 \right[$ .
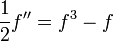tanh est une solution de l'équation différentielle $\frac {1}{2} f'' = f^3 -f$ .

Développement en série de Taylor

tanh est infiniment dérivable :

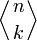$\tanh^{(n)}(0)=\sum_{k=0}^{n-1} \left(-1\right)^k \left \langle {n\atop k} \right \rangle$

où $\left \langle {n\atop k} \right \rangle$ est le nombre de permutations de ${1,..., n}$ dans lesquelles k éléments exactement sont plus grands que l'élément précédent (nombres d'Euler).

tanh possède donc un développement en série de Taylor en tout point :

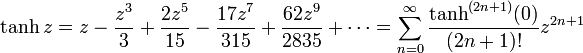$\tanh z = z - \frac {z^3} {3} + \frac {2 z^5} {15} - \frac {17 z^7} {315} + \frac {62 z^9} {2835}+ \cdots = \sum_{n=0}^\infty \frac {\tanh^{(2n+1)}(0)} {(2n+1)!} z^{2n+1}$ .

Développement en fraction continue

La restriction de tanh à $\mathbb R$ admet un développement en fraction continue :

$\tanh x=\frac {x} {1+\frac {x^2} {3+\frac {x^3} {5+\cdots} } }$

Valeurs

Quelques valeurs de tanh :

$\tanh(0) = 0 \,$
$\tanh(1) = \frac {e^2-1} {e^2+1}$
$\tanh(i) = i \tan(1) \,$

Fonction réciproque

tanh admet une fonction réciproque, notée argtanh. Il s'agit d'une fonction à valeurs multiples complexe. Sa branche principale est généralement choisie en posant comme coupure les segments $\left]-\infty ;-1\right[$ et $\left]1;+\infty \right[$ .

$\operatorname{argtanh}(z) = \frac {1}{2} \left( \ln(1+z)-\ln(1-z) \right)$

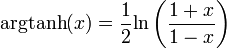Pour $x \in \left]-1;1 \right[$ , la restriction de tanh à $\mathbb R$ admet une réciproque : $\operatorname{argtanh}(x)=\frac {1}{2} \operatorname{ln}\left( \frac {1+x} {1-x} \right)$ .

Voir aussi

Portail des mathématiques

Ce document provient de « Tangente hyperbolique ».

Catégories : Géométrie hyperbolique | Trigonométrie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Tanh de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

tanh — tanh, Funktionszeichen für den Hyperbeltangens (Tangens hyperbolicus), eine Hyperbelfunktion … Universal-Lexikon
Tanh — Tangens Hyperbolicus und Kotangens Hyperbolicus sind Hyperbelfunktionen. Man nennt sie auch Hyperbeltangens oder hyperbolischen Tangens bzw. Hyperbelkotangens oder hyperbolischen Kotangens. Inhaltsverzeichnis 1 Schreibweisen 2 Definitionen 3… … Deutsch Wikipedia
Tanh-sinh quadrature — is a method for numerical integration introduced by Hidetosi Takahasi and Masatake Mori in 1974.[1] It uses the change of variables to transform an integral on the interval x ∈ (−1, +1) to an integral on the entire real line… … Wikipedia
Tanh Linh — ( vi. Tánh Linh), is a district ( huyện ) of Binh Thuan Province in the Southeast region of Vietnam. The district is famous for the Tanh Linh national park … Wikipedia
tanh — Symbol, Math. hyperbolic tangent. [TAN(GENT) + H(YPERBOLIC)] * * * … Universalium
TANH — Hyperbolic Tangent (Academic & Science » Mathematics) … Abbreviations dictionary
tanh — [tan eɪtʃ, tanʃ, θan] abbreviation Mathematics hyperbolic tangent … English new terms dictionary
tanh — /θæn/ (say than), /tænˈeɪtʃ/ (say tan aych) noun See hyperbolic function …
TANH — Semiz olmak, besili ve şişman olmak. * Yemeğin hazmolmaması, sindirilmemesi … Yeni Lügat Türkçe Sözlük
tanh — abbr. hyperbolic tangent … Useful english dictionary

Dictionnaires et Encyclopédies sur 'Academic'

Tanh

Tangente hyperbolique

Sommaire

Définition