- Série zeta rationnelle
-
Série zêta rationnelle
En mathématiques, une série zêta rationnelle est la représentation d'un nombre réel arbitraire en termes d'une série constituée de nombres rationnels et de la fonction zêta de Riemann ou de la fonction zêta d'Hurwitz. Plus précisément, pour un nombre réel donné x, la série zêta ratonelle pour x est donnée par
où
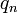 est un nombre rationnel, la valeur m reste fixée et
est un nombre rationnel, la valeur m reste fixée et 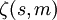 est la fonction zêta d'Hurwitz. Il n'est pas difficile de montrer que tout nombre réel x peut être développé de cette manière. Pour m entier, on a
est la fonction zêta d'Hurwitz. Il n'est pas difficile de montrer que tout nombre réel x peut être développé de cette manière. Pour m entier, on aPour m=2, beaucoup de nombres intéressants ont une expression simple sous forme de série zêta rationnelle :
et
où
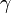 est la constante d'Euler-Mascheroni. Il existe aussi une série pour
est la constante d'Euler-Mascheroni. Il existe aussi une série pour 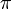 :
:et
devient notable à cause de sa convergence rapide. Cette dernière série se déduit de l'identité générale
qui peut être transformée à partir de la fonction génératrice des nombres de Bernoulli
Adamchik et Srivastava donnent une série similaire
Sommaire
Séries reliées à la fonction polygamma
Un nombre de relations supplémentaires peuvent être déduites à partir des séries de Taylor pour la fonction polygamma au point z=1, qui est
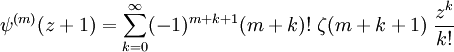 .
.
Ceci converge pour |z|<1. Un cas particulier est
qui reste valide pour | t | < 2. Ici,
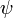 est la fonction digamma et
est la fonction digamma et 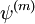 est la fonction polygamma. Beaucoup de séries impliquant les coefficient binomiaux peuvent être dérivés :
est la fonction polygamma. Beaucoup de séries impliquant les coefficient binomiaux peuvent être dérivés :où
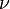 est un nombre complexe. Ceci est issu du développement en série de la fonction zêta d'Hurwitz
est un nombre complexe. Ceci est issu du développement en série de la fonction zêta d'Hurwitzpris à y = − 1. Des séries similaires peuvent être obtenues simplement en algèbre :
et
et
et
Pour
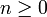 entier, la série
entier, la sériepeut être écrite comme une série finie
Ceci se déduit d'une simple relation récursive
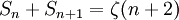 . Ensuite, la série
. Ensuite, la sériepeut être écrite sous la forme
pour
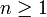 entier. Ceci se déduit à partir de l'identité
entier. Ceci se déduit à partir de l'identité 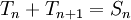 . Ce processus peut être appliqué récursivement pour obtenir des séries finies pour les expressions générales de la forme
. Ce processus peut être appliqué récursivement pour obtenir des séries finies pour les expressions générales de la formepour les nombres entiers positifs m.
Séries de puissances demi-entières
Des séries similaires peuvent êtres obtenues en explorant la fonction zêta d'Hurwitz pour les valeurs demi-entières. Ainsi, par exemple, on a
Expressions sous la forme de séries p
Adamchik et Srivastava donnent
et
où
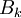 sont les nombres de Bernoulli et
sont les nombres de Bernoulli et 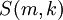 sont les nombres de Stirling de deuxième espèce.
sont les nombres de Stirling de deuxième espèce.Autres séries
D'autres constantes ont des séries zêta rationnelles remarquables :
Références
- Jonathan M. Borwein, David M. Bradley, Richard E. Crandall, sur Computational Strategies for the Riemann Zeta Function
- Victor S. Adamchik and H. M. Srivastava, Some series of the zeta and related functions
- Portail des mathématiques
Catégorie : Fonction zêta
Wikimedia Foundation. 2010.

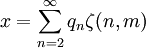
![x=\sum_{n=2}^\infty q_n \left[\zeta(n)- \sum_{k=1}^{m-1} k^{-n}\right]](/pictures/frwiki/100/dc326fefdb1ff714f1317d1586d36533.png)
![1=\sum_{n=2}^\infty \left[\zeta(n)-1\right]](/pictures/frwiki/97/a9809620b090aff95cf5870d0cbd53f8.png)
![1-\gamma=\sum_{n=2}^\infty \frac{1}{n}\left[\zeta(n)-1\right]](/pictures/frwiki/98/b8110c6df07dd108aa09de41cc94ae9b.png)
![\log \pi =\sum_{n=2}^\infty \frac{2(3/2)^n-3}{n}\left[\zeta(n)-1\right]](/pictures/frwiki/52/49d6bfacf1f47c6d5419b1a49f167543.png)
![\frac{13}{30} - \frac{\pi}{8} =\sum_{n=1}^\infty \frac{1}{4^{2n}}\left[\zeta(2n)-1\right]](/pictures/frwiki/53/5ec38e08bb37819a1519afc2bc94628b.png)
![\sum_{n=1}^\infty (-1)^{n} t^{2n} \left[\zeta(2n)-1\right] =
\frac{t^2}{1+t^2} + \frac{1-\pi t}{2} - \frac {\pi t}{e^{2\pi t} -1}](/pictures/frwiki/53/5c05dc349ea17381bfb7c8be41ac56db.png)
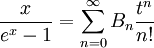
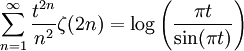
![\sum_{n=2}^\infty t^n \left[\zeta(n)-1\right] =
-t\left[\gamma +\psi(1-t) -\frac{t}{1-t}\right]](/pictures/frwiki/54/6aa5066cf2109dc4b7ce3eb375da2271.png)
![\sum_{k=0}^\infty {k+\nu+1 \choose k} \left[\zeta(k+\nu+2)-1\right]
= \zeta(\nu+2)](/pictures/frwiki/54/6083a96c4d16d1a46a9ac8465e362a56.png)
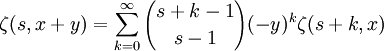
![\sum_{k=0}^\infty {k+\nu+1 \choose k+1} \left[\zeta(k+\nu+2)-1\right]
= 1](/pictures/frwiki/48/07a6bdb619a2051c32f6ac4fc353a64a.png)
![\sum_{k=0}^\infty (-1)^k {k+\nu+1 \choose k+1} \left[\zeta(k+\nu+2)-1\right]
= 2^{-(\nu+1)}](/pictures/frwiki/98/b1e72d52d388a9369c22a7b7b51c963d.png)
![\sum_{k=0}^\infty (-1)^k {k+\nu+1 \choose k+2} \left[\zeta(k+\nu+2)-1\right]
= \nu \left[\zeta(\nu+1)-1\right] - 2^{-\nu}](/pictures/frwiki/101/efaf0e56b321e849e4cca320a3d902d9.png)
![\sum_{k=0}^\infty (-1)^k {k+\nu+1 \choose k} \left[\zeta(k+\nu+2)-1\right]
= \zeta(\nu+2)-1 - 2^{-(\nu+2)}](/pictures/frwiki/57/9d0bd4745cc7b60bd342249f675679c8.png)
![S_n = \sum_{k=0}^\infty {k+n \choose k} \left[\zeta(k+n+2)-1\right]](/pictures/frwiki/99/cd4c9ea9e94b683c4479356faaacd392.png)
![S_n=(-1)^n\left[1+\sum_{k=1}^n \zeta(k+1) \right]](/pictures/frwiki/56/830a2de515ba4efd339e34ebe707b4ea.png)
![T_n = \sum_{k=0}^\infty {k+n-1 \choose k} \left[\zeta(k+n+2)-1\right]](/pictures/frwiki/53/570a6c491f32ce23187c1f5026d09c59.png)
![T_n=(-1)^{n+1}\left[n+1-\zeta(2)+\sum_{k=1}^{n-1} (-1)^k (n-k) \zeta(k+1) \right]](/pictures/frwiki/97/ad3fcc1408f9bba0ae94d987cb0bdd10.png)
![\sum_{k=0}^\infty {k+n-m \choose k} \left[\zeta(k+n+2)-1\right]](/pictures/frwiki/57/931aaa7f091b210dca114f638a52de48.png)
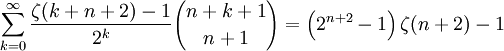
![\sum_{n=2}^\infty n^m \left[\zeta(n)-1\right] =
1\, +
\sum_{k=1}^m k!\; S(m+1,k+1) \zeta(k+1)](/pictures/frwiki/100/d5eeaccd84a9aac8ebd084d06b0b4340.png)
![\sum_{n=2}^\infty (-1)^n n^m \left[\zeta(n)-1\right] =
-1\, +\, \frac {1-2^{m+1}}{m+1} B_{m+1}
\,- \sum_{k=1}^m (-1)^k k!\; S(m+1,k+1) \zeta(k+1)](/pictures/frwiki/57/9311fc7e6c620658e204cd8e5283e18b.png)