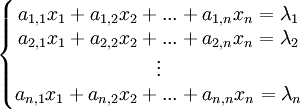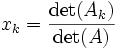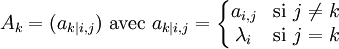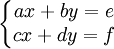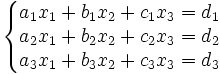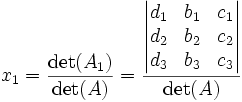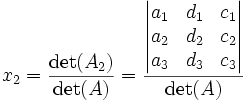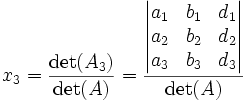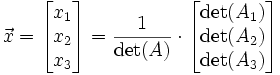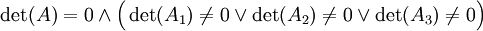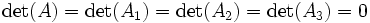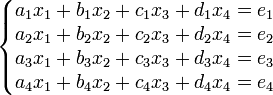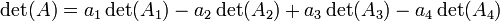Système de Cramer

Règle de Cramer

Pour les articles homonymes, voir Cramer.

La règle de Cramer (ou méthode de Cramer) est un théorème en algèbre linéaire qui donne la solution d'un système d'équations linéaires en termes de déterminants.

En calcul, elle est généralement inefficace et donc n'est pas utilisée en applications pratiques qui pourraient impliquer plusieurs équations (utilisation de la méthode de résolution de Gauss). Cependant, elle est d'importance théorique pour la raison qu'elle donne une expression explicite pour la solution du système.

Elle est nommée d'après Gabriel Cramer, mathématicien suisse (1704-1752).

Description

Le système de n équations à n inconnues, de forme générale :

$\left\{\begin{matrix} a_{1,1}x_1+a_{1,2}x_2+...+a_{1,n}x_n = \lambda_1 \\ a_{2,1}x_1+a_{2,2}x_2+...+a_{2,n}x_n = \lambda_2 \\ \vdots \\ a_{n,1}x_{1}+a_{n,2}x_{2}+...+a_{n,n}x_n = \lambda_n \end{matrix}\right.$

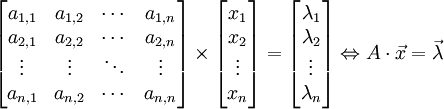
est représenté sous la forme d'un produit matriciel :

$\begin{bmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n}\\ a_{2,1} & a_{2,2} & \cdots & a_{2,n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n,1} & a_{n,2} & \cdots & a_{n,n}\\ \end{bmatrix} \times \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n\\ \end{bmatrix} = \begin{bmatrix} \lambda_1\\ \lambda_2\\ \vdots\\ \lambda_n\\ \end{bmatrix} \Leftrightarrow A \cdot \vec x = \vec \lambda$

où la matrice A, carrée et inversible (déterminant non nul), contient les coefficients des inconnues, le vecteur colonne x contient ces inconnues et le vecteur colonne $λ$ contient les membres de droite des équations du système.

Le théorème affirme alors que:

$x_k = { \det(A_k) \over \det(A) }$

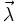où $A k$ est la matrice carrée formée en remplaçant la k^ème colonne de $A$ par le vecteur colonne $\vec \lambda$ .

$A_k = ( a_{k|i,j} ) \mbox{ avec } a_{k|i,j} = \left\{\begin{matrix} a_{i,j} & \mbox{si } j \ne k \\ \lambda_{i} & \mbox{si }j = k\end{matrix}\right.$

Par extension, un système de Cramer est un système qui répond à la condition que le déterminant de la matrice A soit non nul.

Le système admet une infinité de solutions si tous les déterminants des matrices du système sont nuls.
Le système n'admet aucune solution si le déterminant de A est nul et qu'au moins un déterminant d'une matrice $A k$ est non nul.

Le nombre d'opérations à effectuer pour résoudre un système linéaire à l'aide de la règle de Cramer dépend de la méthode utilisée pour calculer le déterminant. Une méthode efficace pour les calculs de déterminant est l'élimination de Gauss-Jordan (complexité polynomiale). Cependant, la règle de Cramer demandera d'avoir recours à un nombre de calculs de déterminants égal à la taille du système, une élimination de Gauss-Jordan appliquée directement au système résout donc le problème plus efficacement.

Exemples

Système d'ordre 2

Soit :

$\left\{\begin{matrix} ax+by = e\\ cx+dy = f\end{matrix}\right.$

alors :

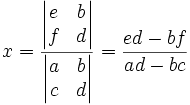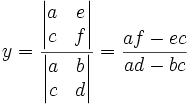
$x = { \begin{vmatrix}e&b\\f&d\end{vmatrix} \over \begin{vmatrix}a&b\\c&d\end{vmatrix} } = { ed - bf \over ad - bc}$ et $y = { \begin{vmatrix}a&e\\c&f\end{vmatrix} \over \begin{vmatrix}a&b\\c&d\end{vmatrix} } = { af - ec \over ad - bc}$

Exemple numérique :

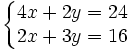
$\left\{\begin{matrix} 4x + 2y = 24\\ 2x + 3y = 16\end{matrix}\right.$

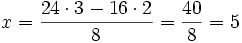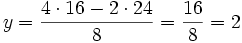
$x = {24 \cdot 3-16 \cdot 2 \over 8 } = {40 \over 8} = 5$ et $y = {4 \cdot 16-2 \cdot 24 \over 8} = {16 \over 8} = 2$

Système d'ordre 3

Soit :

$\left\{\begin{matrix}a_1x_1 + b_1x_2 + c_1x_3 = d_1\\ a_2x_1 + b_2x_2 + c_2x_3 = d_2\\ a_3x_1 + b_3x_2 + c_3x_3 = d_3\end{matrix}\right.$

Posons :

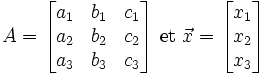$A = \begin{bmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{bmatrix} \mbox{ et }\vec x = \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}$ .

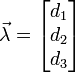
et $\vec \lambda = \begin{bmatrix} d_1\\ d_2\\ d_3 \end{bmatrix}$

Le système admet une solution unique ssi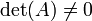 $\det(A) \ne 0$ :

$x_1 = \frac{\det(A_1)}{\det(A)} = \frac{\begin{vmatrix}d_1&b_1&c_1\\d_2&b_2&c_2\\d_3&b_3&c_3\end{vmatrix}}{\det(A)}$

$x_2 = \frac{\det(A_2)}{\det(A)} = \frac{\begin{vmatrix}a_1&d_1&c_1\\a_2&d_2&c_2\\a_3&d_3&c_3\end{vmatrix}}{\det(A)}$

$x_3 = \frac{\det(A_3)}{\det(A)} = \frac{\begin{vmatrix}a_1&b_1&d_1\\a_2&b_2&d_2\\a_3&b_3&d_3\end{vmatrix}}{\det(A)}$

Ou plus simplement :

$\vec x = \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix} = \frac{1}{\det(A)} \cdot \begin{bmatrix} \det(A_1)\\ \det(A_2)\\ \det(A_3)\end{bmatrix}$

Le système n'admet aucune solution si :

$\det(A) = 0 \land \Big( \det(A_1) \ne 0 \lor \det(A_2) \ne 0 \lor \det(A_3) \ne 0 \Big)\,$

Dans le cas

$\det(A) = \det(A_1) = \det(A_2) = \det(A_3) = 0\,$

on peut avoir ou une infinité de solutions ou aucune solution.

Système d'ordre 4

Le calcul du déterminant du système d'ordre 4 est basé sur la méthode du système d'ordre 3,utilisant les coordonnées du 1er vecteur vertical comme coefficients de signe alterné. Soit :

$\left\{\begin{matrix}a_1x_1 + b_1x_2 + c_1x_3 + d_1x_4 = e_1\\ a_2x_1 + b_2x_2 + c_2x_3 + d_2x_4 = e_2\\ a_3x_1 + b_3x_2 + c_3x_3 + d_3x_4 = e_3\\ a_4x_1 + b_4x_2 + c_4x_3 + d_4x_4= e_4\end{matrix}\right.$

Posons :

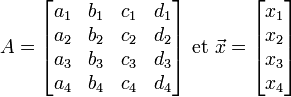$A = \begin{bmatrix}a_1&b_1&c_1&d_1\\a_2&b_2&c_2&d_2\\a_3&b_3&c_3&d_3\\a_4&b_4&c_4&d_4\end{bmatrix} \mbox{ et }\vec x = \begin{bmatrix}x_1\\x_2\\x_3\\x_4\end{bmatrix}$ .

$\det(A) = a_1\det(A_1)-a_2\det(A_2)+a_3\det(A_3)-a_4\det(A_4)\,$

Ce document provient de « R%C3%A8gle de Cramer ».

Catégories : Déterminant | Algèbre multilinéaire | Théorème de mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Système de Cramer de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

cramer — [ krame ] v. <conjug. : 1> • 1823; mot région. du Centre, var. dial. de cremer (XVIe); lat. cremare « brûler » ♦ Fam. 1 ♦ V. tr. Brûler légèrement. Cramer un rôti. Cramer du linge en le repassant. ⇒ roussir. Intrans. Les carottes ont cramé … Encyclopédie Universelle
Systeme d'equations lineaires — Système d équations linéaires En mathématiques et particulièrement en algèbre linéaire, un système d équations linéaires est un ensemble d équations linéaires. Par exemple : Le problème est de trouver les valeurs des inconnues x1, x2 et x3… … Wikipédia en Français
Système d'équations linéaires — En mathématiques et particulièrement en algèbre linéaire, un système d équations linéaires est un ensemble d équations linéaires qui portent sur les mêmes inconnues. Par exemple : Le problème est de trouver les valeurs des inconnues x1, x2… … Wikipédia en Français
Méthode de Cramer — Règle de Cramer Pour les articles homonymes, voir Cramer. La règle de Cramer (ou méthode de Cramer) est un théorème en algèbre linéaire qui donne la solution d un système d équations linéaires en termes de déterminants. En calcul, elle est… … Wikipédia en Français
Regle de Cramer — Règle de Cramer Pour les articles homonymes, voir Cramer. La règle de Cramer (ou méthode de Cramer) est un théorème en algèbre linéaire qui donne la solution d un système d équations linéaires en termes de déterminants. En calcul, elle est… … Wikipédia en Français
Règle de cramer — Pour les articles homonymes, voir Cramer. La règle de Cramer (ou méthode de Cramer) est un théorème en algèbre linéaire qui donne la solution d un système d équations linéaires en termes de déterminants. En calcul, elle est généralement… … Wikipédia en Français
Règle de Cramer — Pour les articles homonymes, voir Cramer. La règle de Cramer (ou méthode de Cramer) est un théorème en algèbre linéaire qui donne la solution d un système de Cramer, c est à dire un système d équations linéaires avec autant d équations que d… … Wikipédia en Français
Paradoxe de Cramer — En mathématiques, et plus précisément en géométrie algébrique, le paradoxe de Cramer (nommé d après Gabriel Cramer, mais qui avait déjà été remarqué par Maclaurin) affirme que le nombre de points d intersection de deux courbes de haut degré peut… … Wikipédia en Français
Pieter Cramer — Pour les articles homonymes, voir Cramer. Page de Die uitlandische Kapellen voorkomende in de drie Waereld Deelen Asia, Africa en America Pieter Cramer est un commerçant et un en … Wikipédia en Français
Krigeage — Le krigeage est une méthode d’estimation issue de la géostatistique. Le terme krigeage, provient du nom de famille de l ingénieur minier sud africain Daniel Gerhardus Krige[1]. Il a été formalisé pour la prospection minière par Georges… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Système de Cramer

Règle de Cramer

Sommaire

Description