- Stabilité de lyapunov
-
Stabilité de Lyapunov
 Pour les articles homonymes, voir Lyapunov.
Pour les articles homonymes, voir Lyapunov.En mathématique et en automatique, la notion de stabilité de Lyapunov apparait dans l'étude des systèmes dynamiques. L'idée de Aleksandr Lyapunov consiste à dire que si tous les points d'un système démarrent autour d'un point x et que tous ces points restent autour de ce point x, alors x est stable au sens de Lyapunov. De plus, si tous ces points convergent vers x alors x est asymptotiquement stable.
Sommaire
Les stabilités
Il existe des dizaines de types de stabilités différentes pour caractériser l'évolution d'un point vers son état stable. les principaux types de stabilité sont abordés ici.
Soit un système autonome
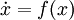 où
où 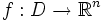 est une application supposée localement lipschitzienne sur
est une application supposée localement lipschitzienne sur 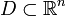 . On suppose que l'origine x = 0 est un point d'équilibre du système qui satisfait
. On suppose que l'origine x = 0 est un point d'équilibre du système qui satisfait 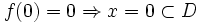 .
.Le point d'équilibre du système
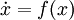 est :
est :- stable au sens de Lyapunov si
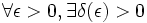 tel que :
tel que : 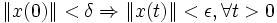
- instable s'il n'est pas stable.
- asymptotiquement stable si le point est stable et que
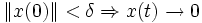 quand
quand 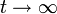
- exponentiellement stable si le point est stable et que :
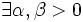 tel que
tel que 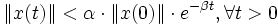
Théorème de Lyapunov (1892)
On présentera ici le théorème sans dépendance temporelle.
S'il existe une fonction dite de Lyapunov
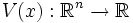 telle que :
telle que :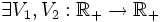 non décroissantes telles que
non décroissantes telles que 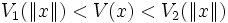
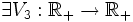 non décroissante et que
non décroissante et que 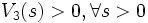 telle que
telle que 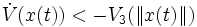
Alors le système est trivialement asymptotiquement stable.
La première condition ne dépend pas du système. En général, la fonction de Lyapunov possède une forme quadratique en x :
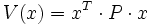 avec P définie positive (P = PT > 0)
avec P définie positive (P = PT > 0)Dans le cas linéaire, si le système est défini par
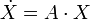 le théorème de Lyapunov est le suivant (formulation originale de Lyapunov) :
le théorème de Lyapunov est le suivant (formulation originale de Lyapunov) :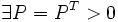 telle que :
telle que : 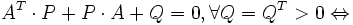 A Hurtwitz
A Hurtwitz 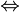 le système est asymptotiquement stable
le système est asymptotiquement stable
On voit ici la puissance du théorème de Lyapunov car il permet de conclure sur la stabilité d'un système dynamique grâce à une équation algébrique. Toute la difficulté est de trouver une fonction de Lyapunov V(x) dans le cas général ou la matrice P dans le cas linéaire. C'est à partir de ce théorème que l'on formule des LMI (Linear Matrix Inequalities) permettant de trouver les matrices adéquates en utilisant des méthodes d'optimisation pour conclure sur la stabilité mais également sur la robustesse des systèmes dynamiques.Le théorème de Lyapunov est aussi à la base des commandes de type sliding mode.
Bibliographie
- A M Liapunov, The General Problem of the Stability of Motion, Taylor & Francis
- Brigitte D'Andréa-Novel , Michel Cohen de Lara, Commande linéaire des systèmes dynamiques, Presses de l'Ecole des Mines de Paris
- Hassan K. Khalil, Non linear Systems, Prentice Hall
Voir aussi
- Portail de l’électricité et de l’électronique
Catégorie : Automatique - stable au sens de Lyapunov si
Wikimedia Foundation. 2010.
